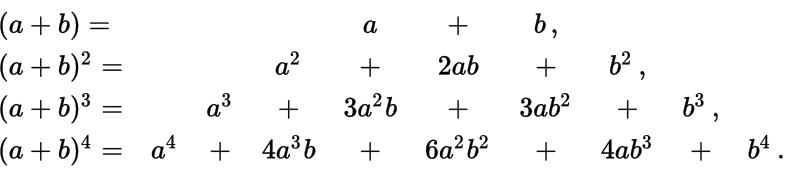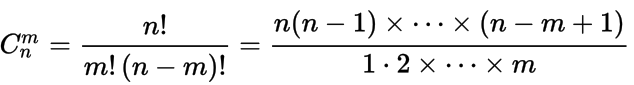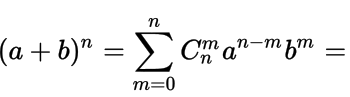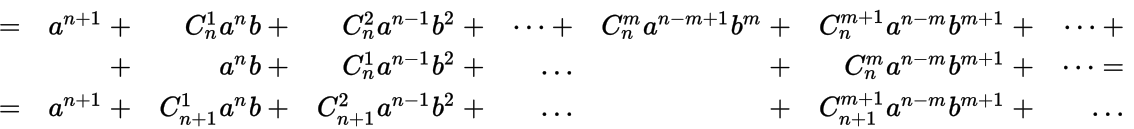История создания треугольной таблицы биномиальных коэффициентов

В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона ( 1 + x ) n {\displaystyle (1+x)^{n}} по степеням x. Коэффициент при x k {\displaystyle x^{k}} обозначается ( n k ) {\displaystyle \textstyle {\binom {n}{k}}} или C n k {\displaystyle \textstyle C_{n}^{k}} и читается «биномиальный коэффициент из n по k» (или «це из n по k»):

(1 + x ) n = ( n 0 ) + ( n 1 ) x + ( n 2 ) x 2 + … + ( n n ) x n = ∑ k = 0 n ( n k ) x k, {\displaystyle (1+x)^{n}={\binom {n}{0}}+{\binom {n}{1}}x+{\binom {n}{2}}x^{2}+\ldots +{\binom {n}{n}}x^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{k},} (1)

для натуральных степеней n {\displaystyle n}. Биномиальные коэффициенты могут быть также определены для произвольных действительных чисел n {\displaystyle n}. В случае произвольного действительного числа n {\displaystyle n} биномиальные коэффициенты определяются как коэффициенты разложения выражение ( 1 + x ) n {\displaystyle (1+x)^{n}} в бесконечный ряд Тейлора:

( 1 + x ) n = ∑ k = 0 ∞ ( n k ) x k, {\displaystyle (1+x)^{n}=\sum _{k=0}^{\infty }{\binom {n}{k}}x^{k},}

Для неотрицательных целых n все коэффициенты с индексами k>n в этом ряду являются нулевыми (т.е. ( n k ) = 0 {\displaystyle \textstyle {\binom {n}{k}}=0} ), и поэтому данное разложение представляет собой конечную сумму (1).

В комбинаторике биномиальный коэффициент ( n k ) {\displaystyle \textstyle {\binom {n}{k}}} для неотрицательных целых чисел n и k интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n-элементном множестве.

Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.