| Математика курсында y=ax+b сызықты функциясының графигі – түзу, квадраттық функциясының графигі – парабола, кері тәуелділіктің графигі гипербола екені көрсетіліп, фигураларды түрлендіру түрлері қарастырылады. Енді осылардың негізінде қарапайым түрлендірулерді қолданып, �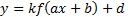 �(мұндағы � �(мұндағы �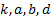 �-нақты сандар) функциясының графигін салу жолын қарастырайық. �-нақты сандар) функциясының графигін салу жолын қарастырайық. �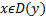 � облысында анықталған � � облысында анықталған �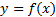 �функциясының графигі қисық болсын. Бұл графикке төмендегідей түрлендірулер қолдануға болады. ................... �функциясының графигі қисық болсын. Бұл графикке төмендегідей түрлендірулер қолдануға болады. ................... y=f(x)+d функциясының графигі y=f(x) функциясының ординаталар осі бойымен �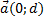 � векторына параллель көшіру арқылы салынады. Демек, � векторына параллель көшіру арқылы салынады. Демек, 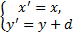
формуласы арқылы әрбір M(x;y) нүктесі �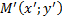 � немесе � � немесе � � нүктесіне көшеді. Егер берілген y=f(x)функциясының графигі � � нүктесіне көшеді. Егер берілген y=f(x)функциясының графигі �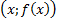 � нүктелерінің геометриялық орны болса, онда � � нүктелерінің геометриялық орны болса, онда �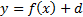 � функциясының графигі � � функциясының графигі �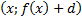 �нүктелерінің геометриялық орны болып табылады. �нүктелерінің геометриялық орны болып табылады. Сонымен, �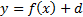 �функциясының графигін салу үшін, егер d0 болса, онда � �функциясының графигін салу үшін, егер d0 болса, онда �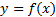 � функциясының графигін Оу ордината осінің бойымен оң бағытта , ал егер d� � функциясының графигін Оу ордината осінің бойымен оң бағытта , ал егер d�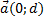 � векторына параллель көшіру керек � векторына параллель көшіру керек II. �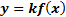 �функциясының графигі Оу осі бойымен к бірлікке созу (сығу) арқылы салынады. Бұл жағдайда �функциясының графигі Оу осі бойымен к бірлікке созу (сығу) арқылы салынады. Бұл жағдайда �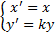 � (2) � (2) формуласы арқылы А(х;у) нүктелері �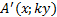 � нүктелеріне көшеді. � � нүктелеріне көшеді. �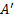 � нүктесін салу үшін А нүктесінің Ох осіндегі � � нүктесін салу үшін А нүктесінің Ох осіндегі � �проекциясын белгілеп аламыз. Енді центрі � �проекциясын белгілеп аламыз. Енді центрі �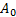 � болатын А-ға гомотетиялы � � болатын А-ға гомотетиялы �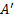 � нүктесін саламыз, гомотетия коэффициенті к-ға тең. Осы сияқты � � нүктесін саламыз, гомотетия коэффициенті к-ға тең. Осы сияқты � �функциясының барлық � �функциясының барлық �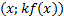 � нүктелері табылады. Осы соңғы нүктелердің геометриялық орны � � нүктелері табылады. Осы соңғы нүктелердің геометриялық орны �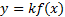 � функциясының графигі болады. � функциясының графигі болады. Сонымен, �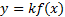 �функциясының графигін салу үшін � �функциясының графигін салу үшін �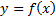 �функциясының графигін Оу осінің бойымен � �функциясының графигін Оу осінің бойымен �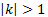 �болғанда,� �болғанда,�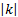 � есе созу және � � есе созу және �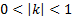 � болғанда, � � болғанда, � � есе қысу керек. � есе қысу керек. III.�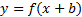 � функциясының графигін салу үшін � � функциясының графигін салу үшін �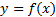 � функциясының графигін абсциссалар осінің бойымен � � функциясының графигін абсциссалар осінің бойымен �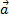 � (-b;0) векторына параллель көшіреді, яғни � (-b;0) векторына параллель көшіреді, яғни �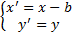 � (3) � (3) Бұл жағдайда �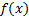 � функциясы графигінің � � функциясы графигінің �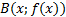 � нүктелері (3) формула бойынша � � нүктелері (3) формула бойынша � � нүктелеріне көшеді, яғни � � нүктелеріне көшеді, яғни �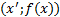 � нүктелерінің геометриялық орны � � нүктелерінің геометриялық орны �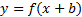 � функциясының графигі болады. � функциясының графигі болады. Сонымен, �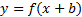 � функциясының графигін � � функциясының графигін �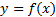 � функциясының Ох осінің бойымен � � функциясының Ох осінің бойымен �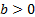 � болғанда, (b;0) векторына теріс бағытта, b � болғанда, (b;0) векторына теріс бағытта, b IV. �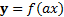 � (мұндағы � � (мұндағы � �) функциясының графигін � �) функциясының графигін �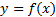 � функциясының графигінен Ох осі бойымен созу (қысу) түрлендіруін қолдану арқылы алады. Бұл түрлендіру кезінде � функциясының графигінен Ох осі бойымен созу (қысу) түрлендіруін қолдану арқылы алады. Бұл түрлендіру кезінде �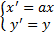 �(4) �(4) формуласы пайдаланылады. Бұл жағдайда �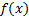 � функциясы графигінің � � функциясы графигінің �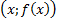 � нүктелері � � нүктелері �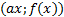 � нүктелеріне көшеді. Бұл нүктелердің геометриялық орны � � нүктелеріне көшеді. Бұл нүктелердің геометриялық орны �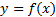 � функциясының графигі болып табылады. Сонымен, � � функциясының графигі болып табылады. Сонымен, � � функциясының графигін � � функциясының графигін �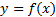 � функциясының графигінен � � функциясының графигінен � � болғанда, � � болғанда, � � есе қысу немесе � � есе қысу немесе � � болғанда, � � болғанда, � � есе созу арқылы алады. � есе созу арқылы алады. | 















