Агадилова Мерует Абибековна
Преподаватель дисциплины «Численные методы»
ГБ ПОУ Байконурский электрорадиотехнический техникум им. М.И.Неделина
Курс 2
Тема занятия: «Понятие о дифференциальном уравнении. Метод Эйлера»
Цели занятия
обучающая:
повторение основных понятий изученных по дисциплине «Высшая математика» по теме «Дифференциальные исчисления»: дифференциальное уравнение, порядок дифференциального уравнения, обыкновенное дифференциальное уравнение, решение дифференциального уравнения, формулировка задачи Коши;
изучение метода Эйлера для решения дифференциальных уравнений;
показать использование информационных технологий при решении дифференциальных уравнений;
показать практические применение полученных знаний в различных дисциплинах специальности: основы алгоритмизации и программирования, информационные технологии;
осуществить контроль за качеством усвоения полученных знаний по изученному материалу;
- сформировать умение осуществлять перенос знаний в измененную ситуацию.
развивающая:
сформировать целостную естественно научную картину специальности через предметные связи математики, информационных технологии и основ алгоритмизации и программирования;
сформировать умение видеть применение абстрактных математических понятий, в частности, математических уравнений, в других предметных областях;
развитие умения анализировать, обобщать и систематизировать материал, выделять главное из изучаемого материала;
развитие познавательного интереса и творческих способностей студентов при создании новых программных продуктов.
воспитательная:
- воспитать уверенность в своих силах, самостоятельность при выполнении вычислений.
методическая:
- показать особенности реализации межпредметного обобщения материала.
Методическое и техническое оснащение
карточки;
проектор;
персональный компьютер.
Тип занятия: изучение нового материала.
Используемая литература
Численные методы. Учебник для техникумов. - М .: Высшая школа, 1976.
Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике.- М.: Высшая школа, 1990.
Численные методы. Калиткин Н. Н. Главная редакция физико-математической литературы. - Наука М., 1978.
ХОД ЗАНЯТИЯ
Организационный момент – 2-3 мин.
Актуализация опорных знаний.
2.1 Фронтальная беседа: (5-6 мин)
На уроках по дисциплине «Высшая математика» вами был изучен раздел «Дифференциальные исчисления». Сегодня мы вспомним этот материал и рассмотрим методы решения дифференциальных уравнений с точки зрения применения этих методов в программировании. (Слайд 1)
-Какое уравнение называется дифференциальным?
Уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называются дифференциальным уравнением.
(Слайд 2)
- Что такое порядок дифференциального уравнения?
Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящей в уравнение.
(Слайд 3)
- Какое дифференциальное уравнение называется обыкновенным?
Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменой, то дифференциальное уравнение называется обыкновенным.
(Слайд 4)
- Какие параметры содержит в общем случае обыкновенное дифференциальное уравнение n-го порядка
Обыкновенное дифференциальное уравнение n-го порядка в самом общем случае содержит независимую переменную x , неизвестную функцию y и ее производные или дифференциалы до n-го порядка включительно и имеет вид
и имеет вид 
(Слайд 5)
- Что называется решением дифференциального уравнения?
Решением (или интегралом) уравнения 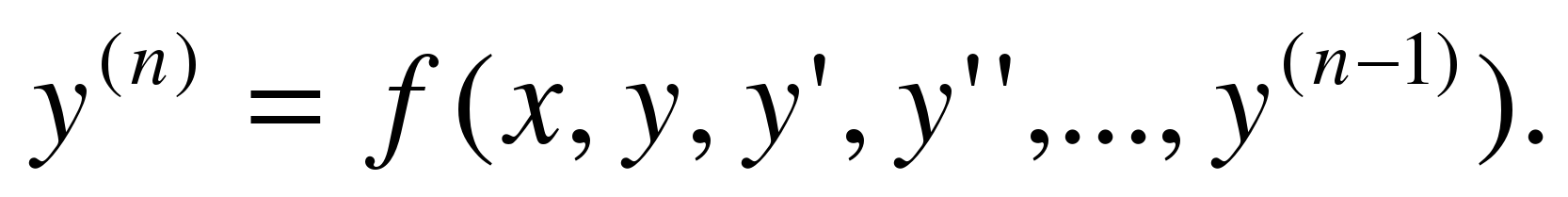 называется всякая дифференцируемая функция
называется всякая дифференцируемая функция  удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение
удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение 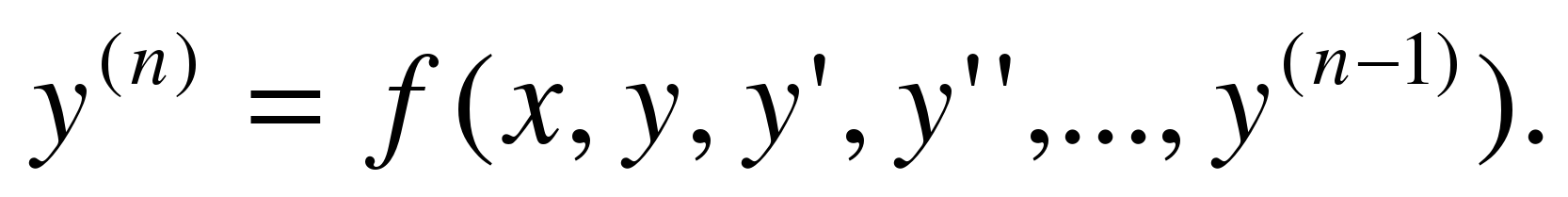 оно обращается в тождество.
оно обращается в тождество.
(Слайд 6)
-Сформулируйте задачу Коши.
Задача с начальными условиями ставится так: найти решение 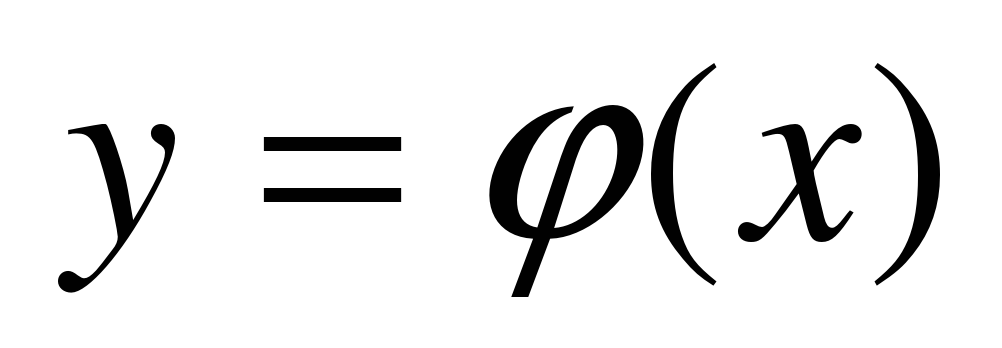 уравнения
уравнения 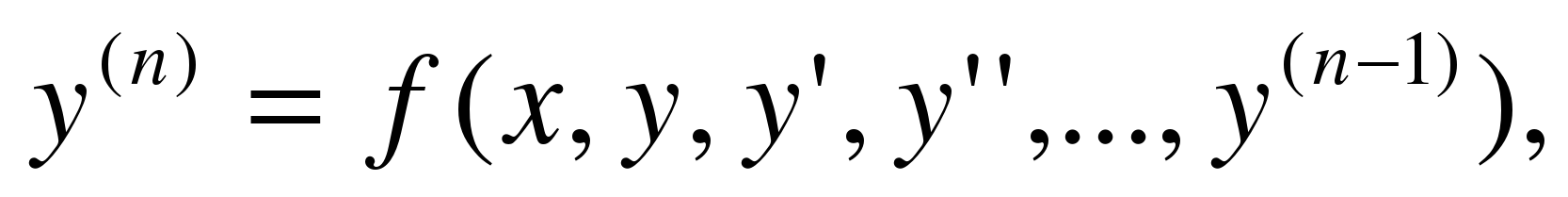 удовлетворяющее дополнительным условиям, состоящим в том, что решение
удовлетворяющее дополнительным условиям, состоящим в том, что решение 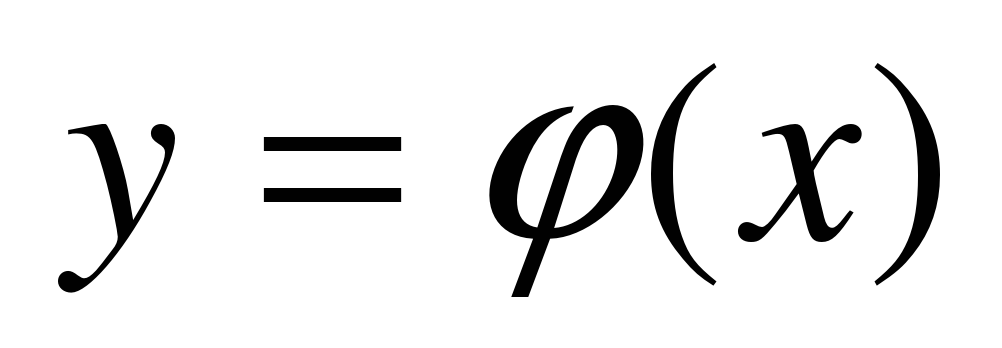 должно принимать вместе со своими производными до (n-1)-го порядка заданные числовые значения
должно принимать вместе со своими производными до (n-1)-го порядка заданные числовые значения 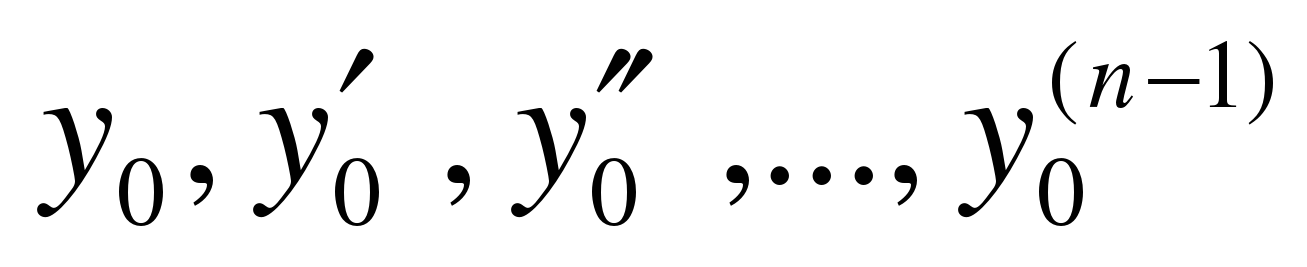 при заданном числовом значении
при заданном числовом значении 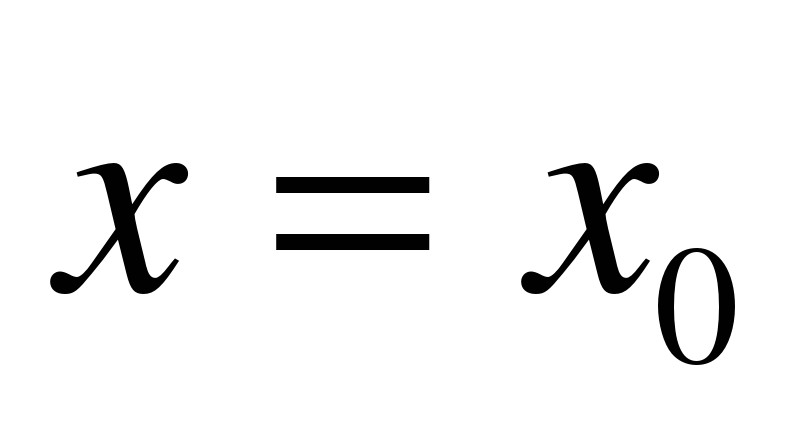 независимой переменной x:
независимой переменной x:  при
при 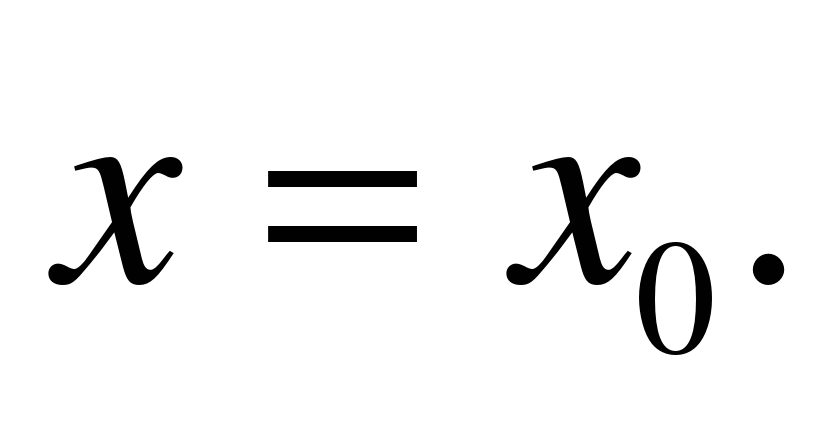 (Слайд 7)
(Слайд 7)
Эти условия называются начальными условиями; числа  ─ начальными данными решения, а задача отыскания решения
─ начальными данными решения, а задача отыскания решения 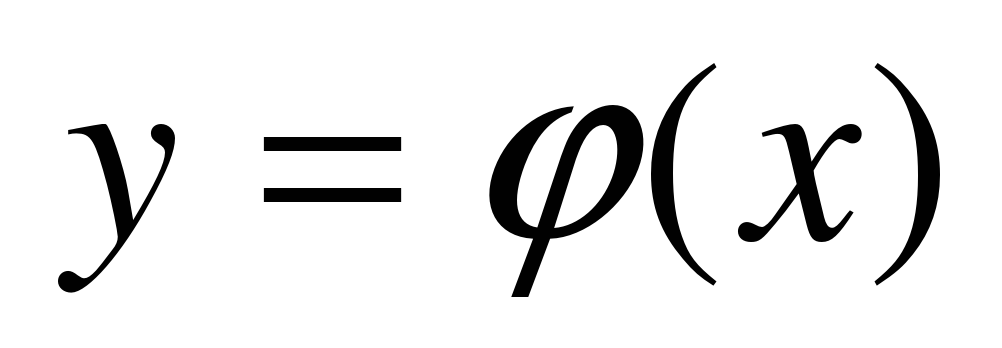 дифференциального уравнения
дифференциального уравнения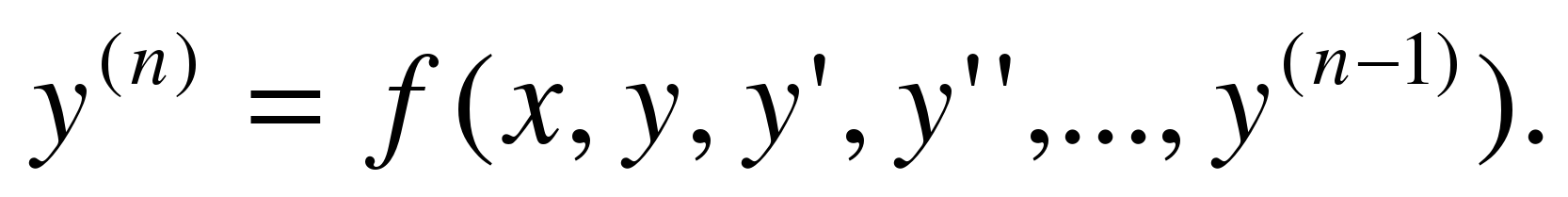 , удовлетворяющего начальным условиям, ─ задачей с начальным условиями, или задачей Коши.
, удовлетворяющего начальным условиям, ─ задачей с начальным условиями, или задачей Коши.
Геометрически задача Коши (для уравнения первого порядка) состоит в том, из всего множества интегральных кривых, представляющих собой общее решение, нужно найти ту интегральную кривую, которая проходит через точку  с координатами
с координатами 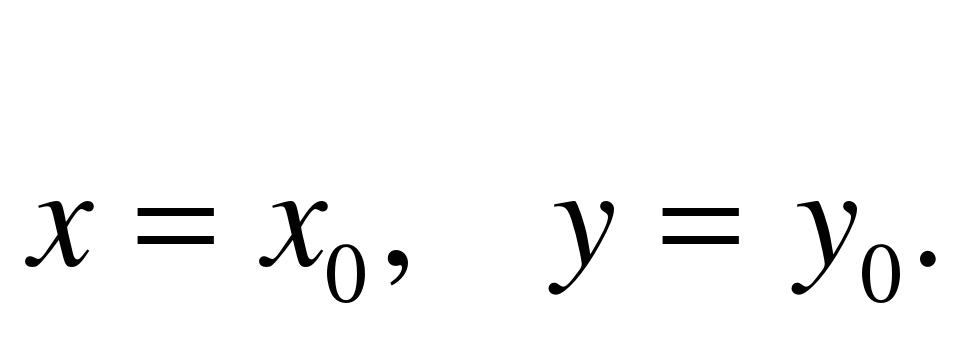
Изучение материала (60 мин)
3.1 Решение дифференциальных уравнений численными методами (5 мин)
Методы точного интегрирования дифференциальных уравнений, изученных вами на дисциплине «Высшая математика» пригодны лишь для сравнительно небольшой части уравнений, встречающихся на практике. Поэтому большое значение приобретают методы приближенного решения дифференциальных уравнений, которые в зависимости от формы представления решения можно разделить на две группы:
аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения;
численные методы, дающие приближенное решение в виде таблицы.
(Слайд 8)
Решить обыкновенное дифференциальное уравнение 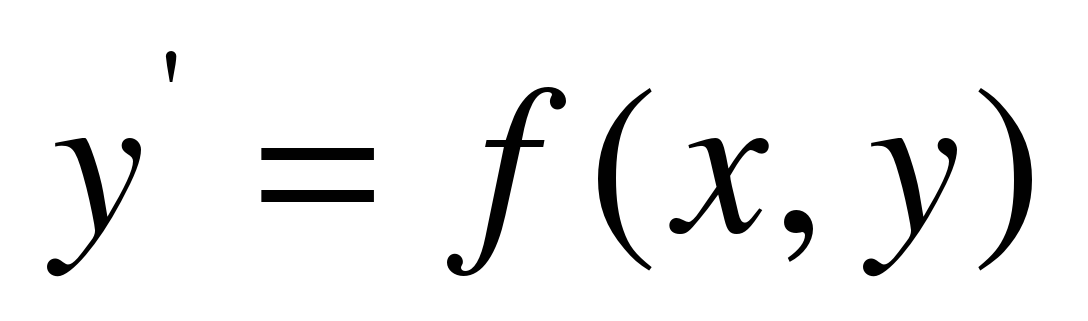 численным методом – это значит для заданной последовательности аргументов
численным методом – это значит для заданной последовательности аргументов 
 и числа
и числа 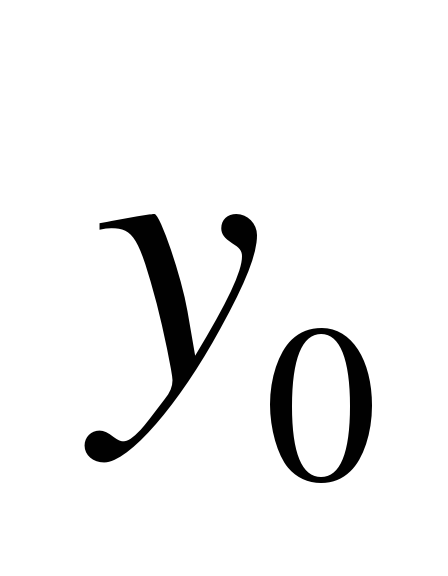 , не определяя функцию
, не определяя функцию 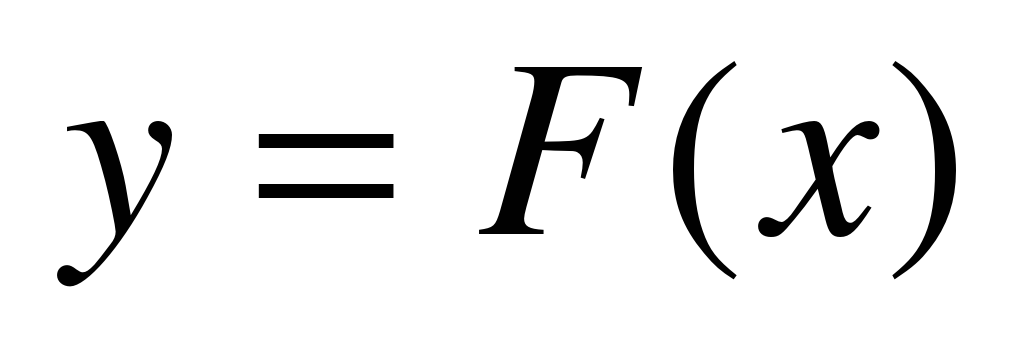 , найти такие значения
, найти такие значения 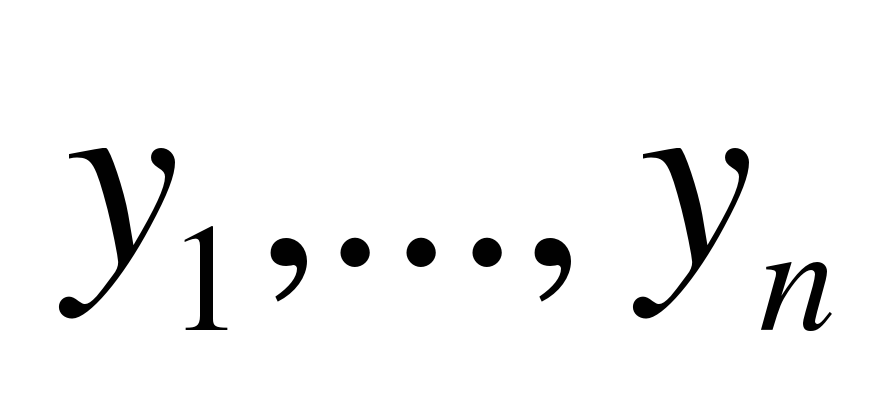 , что
, что 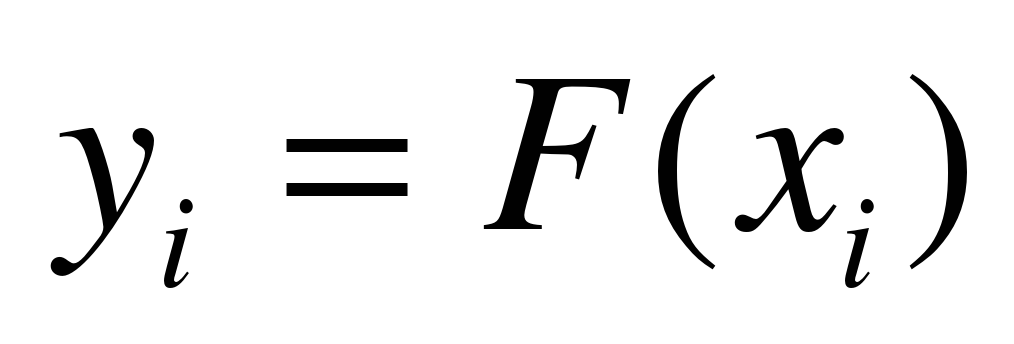
 и
и 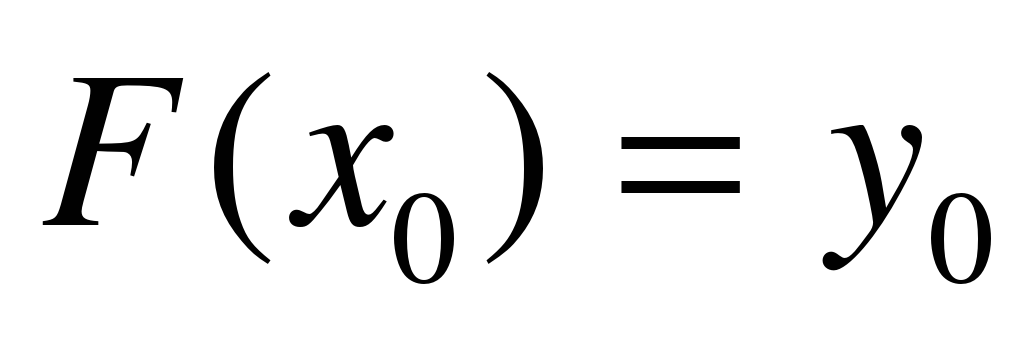 . (Слайд 9)
. (Слайд 9)
Таким образом, численные методы позволяет вместо нахождения функции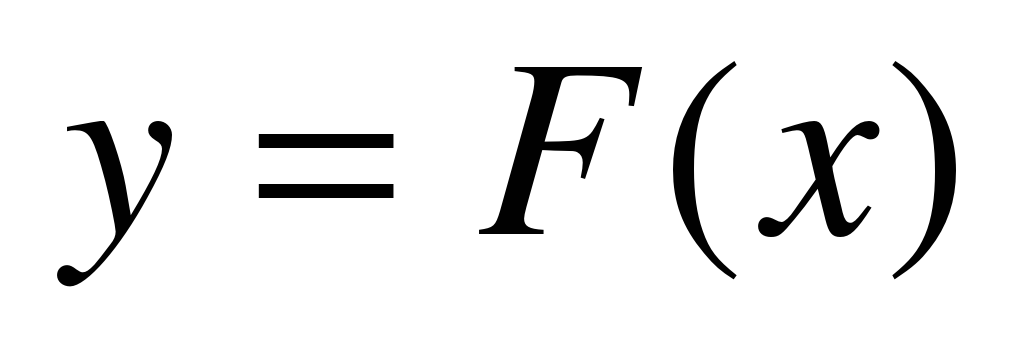 получить таблицу значений этой функции для заданной последовательности аргументов.
получить таблицу значений этой функции для заданной последовательности аргументов.
Существует множество методов численного решения дифференциальных уравнений: Метод Эйлера, различные модификации метода Эйлера, метод Рунге-Кутта, метод Адамса. (Слайд 10)
Рассмотрим метод Эйлера. (Слайд 11)
3.2 Метод Эйлера (30мин)
Метод Эйлера — наиболее простой численный метод решения обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление».
Л.Эйлер (1707-1783)- математик, механик, физик и астроном, ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, теории чисел, небесной механике, математической физике, оптике, балластике, кораблестроению, теории музыки и др. (Слайды 12,13)
Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.
Идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Постановка задачи: Пусть дано обыкновенное дифференциальное уравнение первого порядка 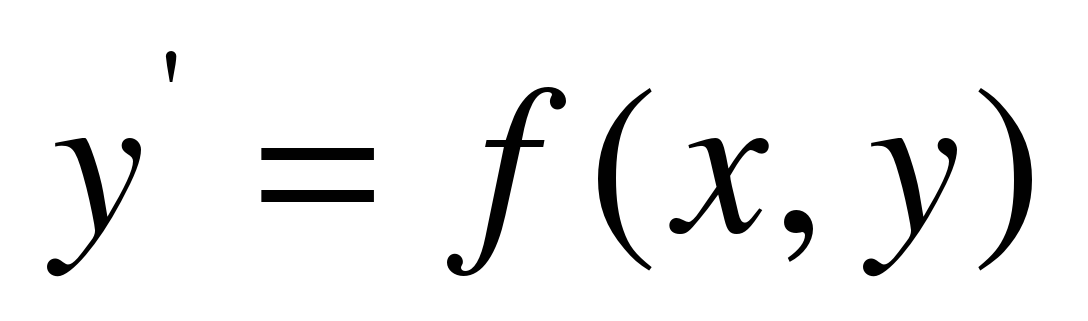 с начальным условием
с начальным условием 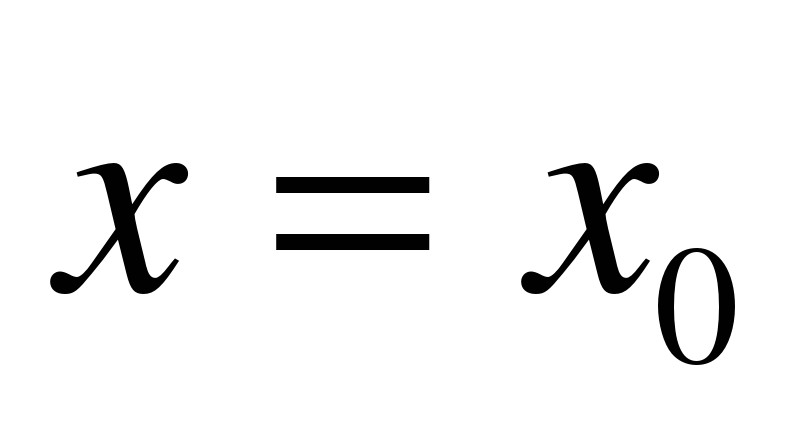
 Требуется найти решение уравнения
Требуется найти решение уравнения 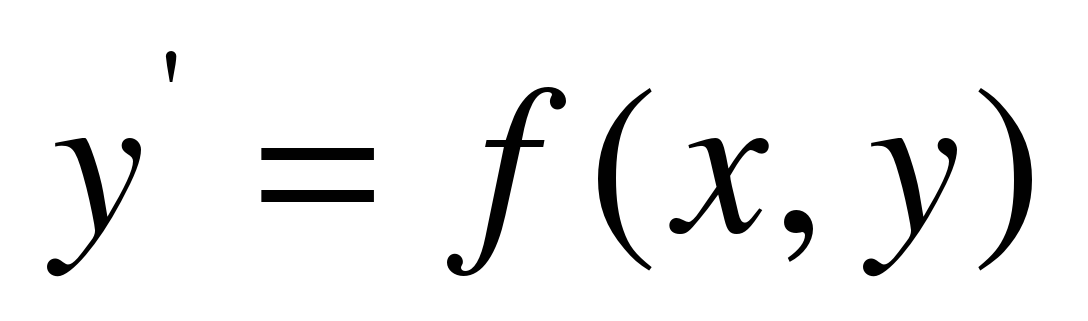 на отрезке [a,b]. (Слайд 14)
на отрезке [a,b]. (Слайд 14)
Разобьем отрезок [a, b] на n равных частей и получим последовательность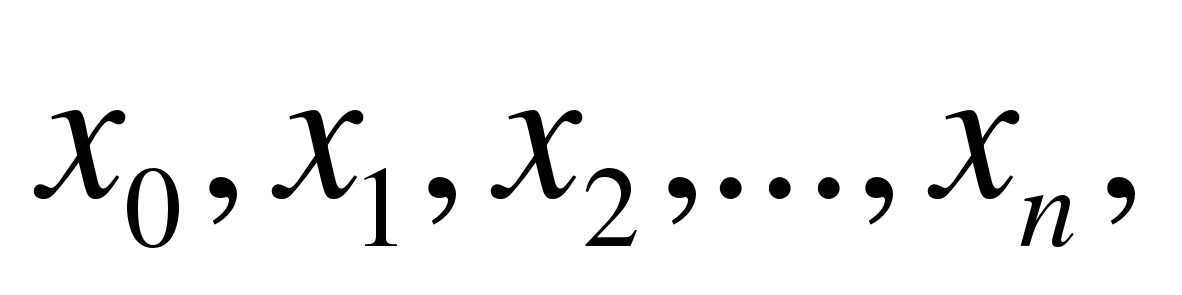 где
где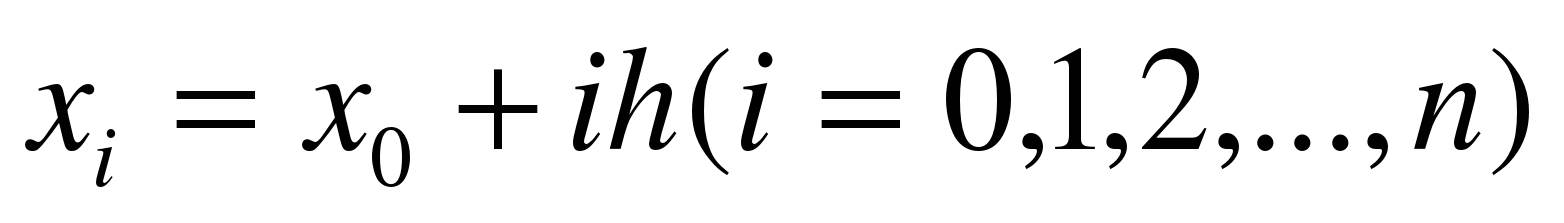 , а
, а 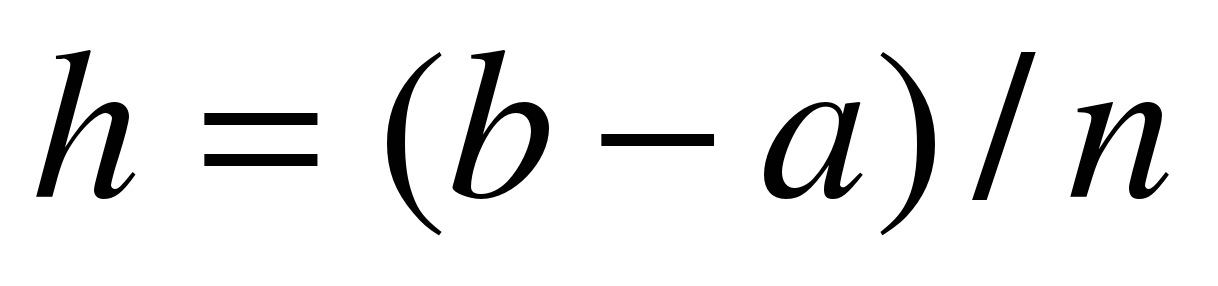 - шаг интегрирования.
- шаг интегрирования.
Выберем 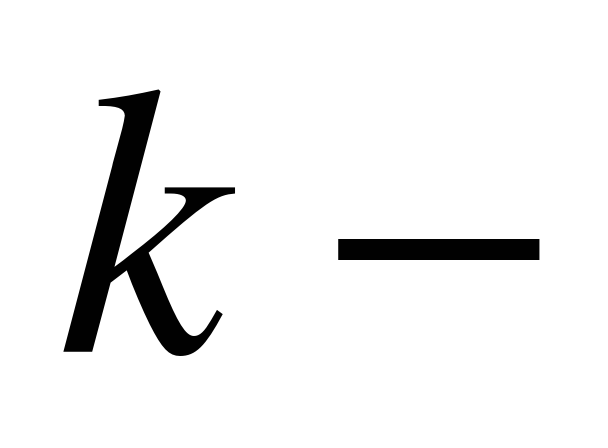 й участок [
й участок [ ] и проинтегрируем уравнение
] и проинтегрируем уравнение 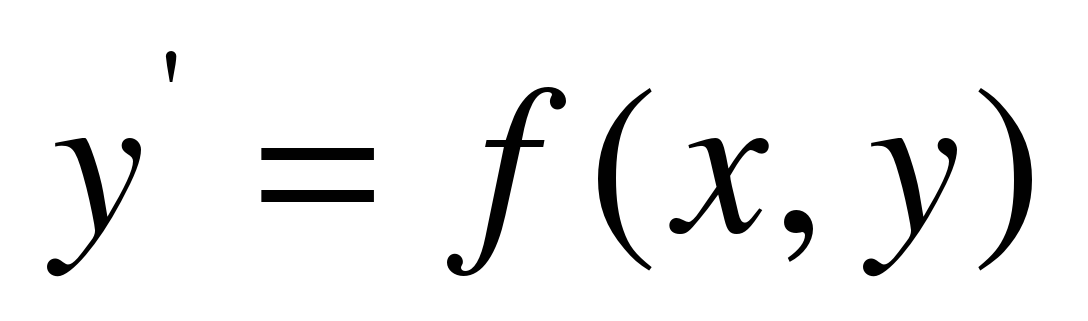 :
: 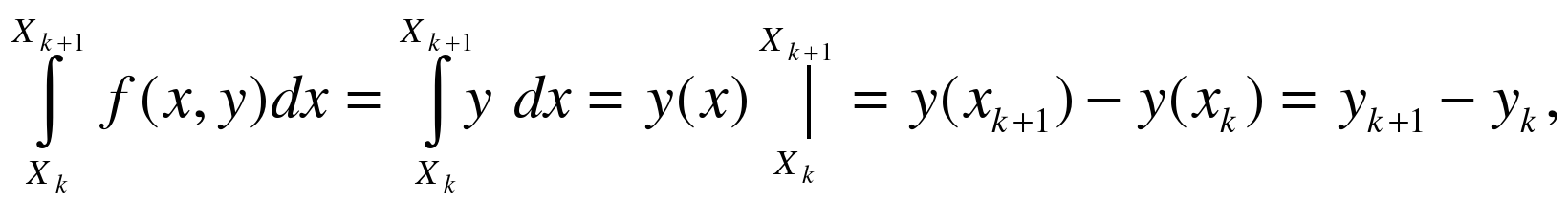
т.е. 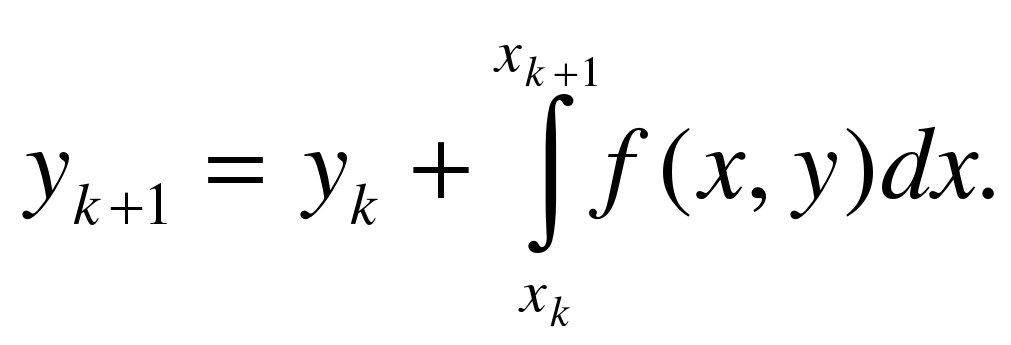 (1)
(1)
Если в последнем интеграле подынтегральную функцию на участке 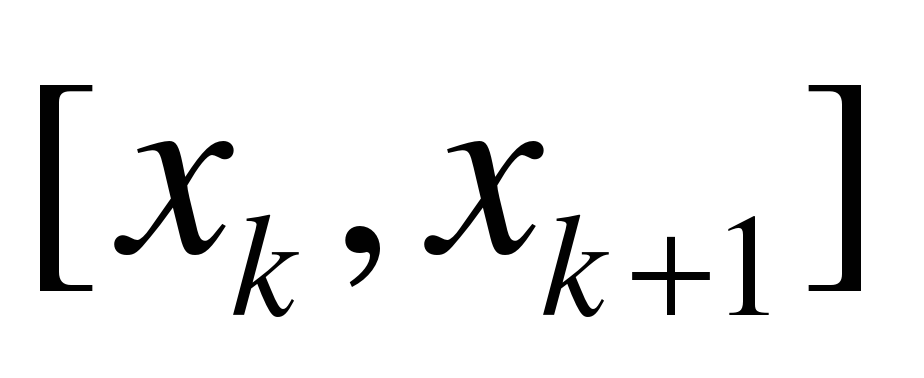 принять постоянной и равной начальному значению в точке
принять постоянной и равной начальному значению в точке  , то получим
, то получим

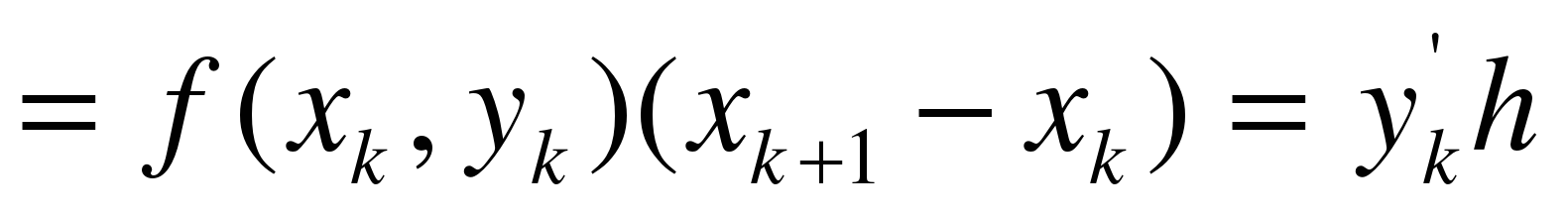 .
.
Тогда формула (1) имеет вид
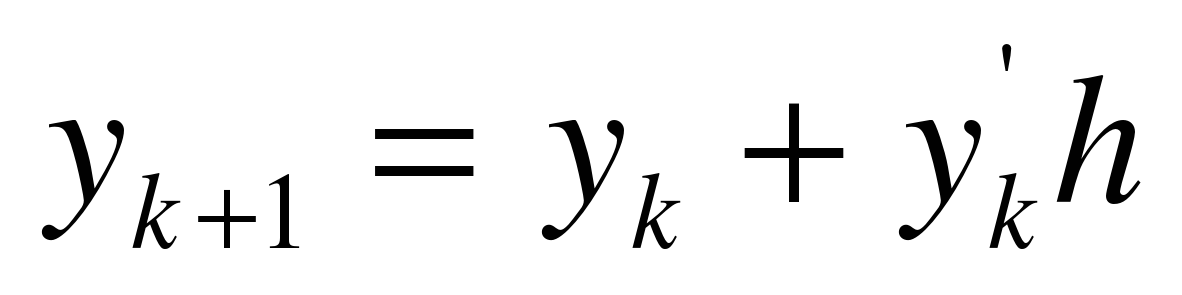 . (2)
. (2)
Продолжая этот процесс и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном отрезке [a,b].
Все вычисления по методу Эйлера удобно располагать в таблице (см. таблицу 1). (Слайд 15)
Таблица 1- Общая схема вычисления по методу Эйлера
| i | xi | yi | y`i=f(xi,yi) | dyi=h*y`i |
| 0 | x0=a | y0 | y`0=f(x0,y0) | h*y`0 |
| 1 | x1=x0+h | y1=y0+ h*y`0 | y`1=f(x1,y1) | h*y`1 |
| 2 | x2=x1+h | y2=y1+ h*y`1 | y`2=f(x2,y2) | h*y`2 |
| … | … | … | … | … |
| n | xn=b | yn=yn-1+ h*y`n-1 |
|
|
Решением дифференциального уравнения являются все значения в столбце yi
3.3 Решение задачи (10 мин)
Пример. Проинтегрировать методом Эйлера дифференциальное уравнение 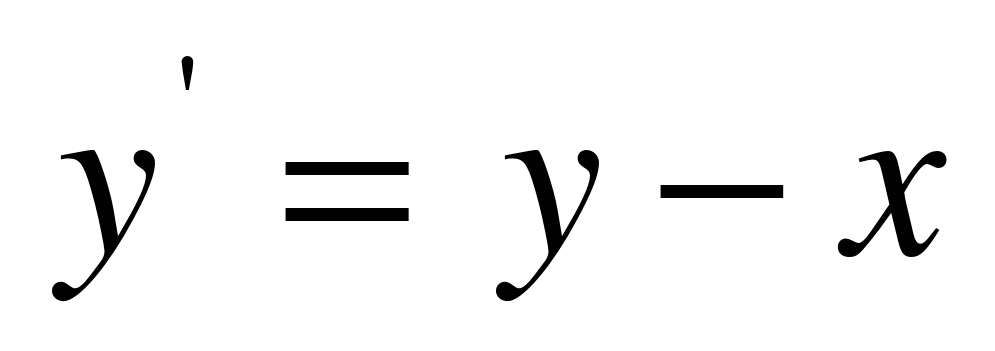 с начальным условием
с начальным условием 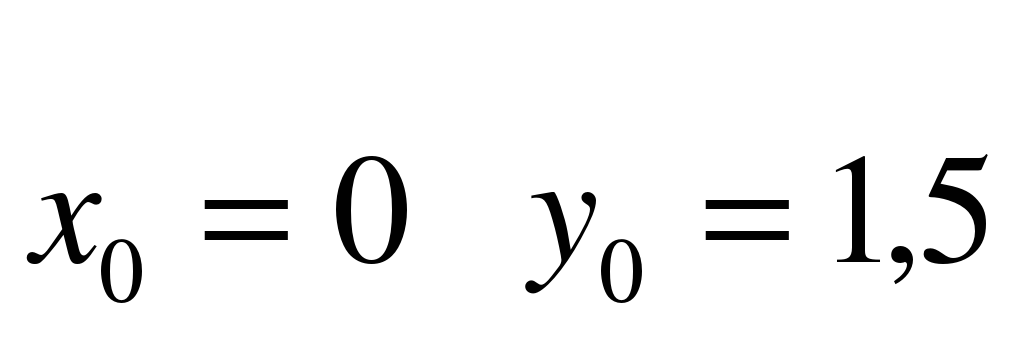 на отрезке[0;1,5], приняв h=0,25. Вычисления вести с четырьмя знаками после запятой. (Слайд 16)
на отрезке[0;1,5], приняв h=0,25. Вычисления вести с четырьмя знаками после запятой. (Слайд 16)
Решение. Для удобства вычислений составим следующую таблицу (см. таблицу 2).
Таблица 2- Решение дифференциального уравнения
| i | xi | yi | y`i=yi-xi | dyi=h*y`i |
| 0 1 2 3 4 5 6 | 0 0,25 0,50 0,75 1,00 1,25 1,50 | 1,5000 1,8750 2,2812 2,7265 3,2206 3,7758 4,4072 | 1,5000 1,6250 1,7812 1,9765 2,2206 2,5258 | 0,3750 0,4062 0,4453 0,4941 0,5552 0,6314 |
Ответ: ответом является весь столбец yi
3.4 Составление алгоритма метода (5 мин)
Теперь давайте составим блок-схему решения дифференциальных уравнений методом Эйлера.
Входными данными в методе являются отрезок интегрирования [a,b], шаг интегрирования h, начальное условие x0, y0.
Каждая итерация состоит из вычисления значения дифференциального уравнения 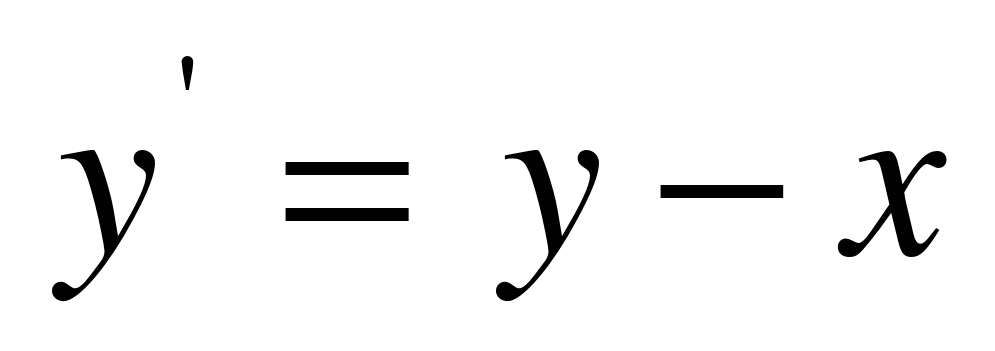 на данном шаге и вычисления значений xi и yi. Всего выполняется
на данном шаге и вычисления значений xi и yi. Всего выполняется  итераций.
итераций.

Рисунок 1- Блок схема алгоритма решения дифференциального уравнения
методом Эйлера
3.5 Решение дифференциального уравнения в MS Excel (5 мин)
Вычислим дифференциальное уравнение при помощи пакета Microsoft Office, а именно программы Microsoft Excel, предназначенный для выполнения математических расчетов. В настоящее время этот пакет вы начали изучать по дисциплине «Информационные технологии». При помощи программы Microsoft Excel очень удобно выполнять вычисления по многим алгоритмам, изучаемым по дисциплине «Численные методы». Для этого обратимся к алгоритму метода,, представленному на рисунке 1, и оформим решение как показано в таблице 1.
(Программа Microsoft Excel проецируется на экран при помощи проектора и осуществляется вычисление дифференциального уравнения с пояснением каждого действия )

Рисунок 2 – Вычисление в Microsoft Excel
3.6 Составление программы на языке Pascal (5 мин)
Теперь попробуем применить знания, полученные по дисциплине «Основы алгоритмизации и программирования», и составим программу для вычисления дифференциального уравнения на языке Паскаль, которому вы посвятили весь 1 семестр курса. Для этого обратимся к алгоритму метода, представленному на рисунке 1.
(Среда программирования Borland Pascal проецируется на экран при помощи проектора и осуществляется набор программы с пояснением каждого оператора )
Листинг программы:
Var i,n: integer;
h,dy,a,b,x,y: real;
begin
writeln('Введите начальное значение отрезка a'); readln(a);
writeln('Введите конечное значение отрезка b'); readln(b);
writeln('Введите шаг интегрирования h'); readln(h);
writeln('Введите начальное условие x0,y0'); readln(x, y);
n:=round((b-a)/h);
for i:=0 to n do begin
dy:=y-x;
writeln(i,' ', x:5:2, ' ', y:5:4,' ', dy:5:4,' ', h*dy:5:4);
y:=y+h*dy;
x:=x+h;
end; end.
Результат работы программы:
Рисунок 3- Результат работы программы
4. Закрепление материала (20 мин)
4.1 Решение дифференциального уравнения методом Эйлера
По желанию один студент выходит к доске, а остальные решают самостоятельно в тетрадях.
Задача. Проинтегрировать методом Эйлера дифференциальное уравнение y`=x+cos(y/3) с начальным условием y(1,6)=4,6 на отрезке[1,6;2,6], приняв h=0,2. Вычисления вести с четырьмя знаками после запятой. (Слайд 17)
Решение:
| I | x | y | y` | dy |
| 0 | 1,6 | 4,6000 | 1,6375 | 0,3275 |
| 1 | 1,8 | 4,9275 | 1,7284 | 0,3457 |
| 2 | 2 | 5,2732 | 1,8142 | 0,3628 |
| 3 | 2,2 | 5,6360 | 1,8970 | 0,3794 |
| 4 | 2,4 | 6,0154 | 1,9792 | 0,3959 |
| 5 | 2,6 | 6,4112 |
|
|
4.2 Самостоятельная работа
(Задания раздаются студентам на карточках)
Вариант 1
Проинтегрировать методом Эйлера дифференциальное уравнение y`=x+y2 с начальным условием y(-2)=0 на отрезке[-2;-1], приняв h=0,2. Вычисления вести с четырьмя знаками после запятой.
Вариант 2
Проинтегрировать методом Эйлера дифференциальное уравнение y`=x(y+2) с начальным условием y(-1)=0 на отрезке[-1;0], приняв h=0,2. Вычисления вести с четырьмя знаками после запятой.
Решения дифференциальных уравнений представлены в приложении А.
5. Задание на дом (2 мин) – (Слайд 18)
работа с опорным конспектом, [Л1, 67-77]
Проинтегрировать методом Эйлера дифференциальное уравнение y`=2(x+y) с начальным условием y(1)=0 на отрезке[1,2], приняв h=0,2. Вычисления вести с четырьмя знаками после запятой.
Приложение А
Решение самостоятельной работы
Вариант 1
| I | x | y | y` | dy |
| 0 | -2 | 0,0000 | -2,0000 | -0,4000 |
| 1 | -1,8 | -0,4000 | -1,6400 | -0,3280 |
| 2 | -1,6 | -0,7280 | -1,0700 | -0,2140 |
| 3 | -1,4 | -0,9420 | -0,5126 | -0,1025 |
| 4 | -1,2 | -1,0445 | -0,1090 | -0,0218 |
| 5 | -1 | -1,0663 |
|
|
Вариант 2
| I | x | y | y` | dy |
| 0 | -1 | 0,0000 | -2,0000 | -0,4000 |
| 1 | -0,8 | -0,4000 | -1,2800 | -0,2560 |
| 2 | -0,6 | -0,6560 | -0,8064 | -0,1613 |
| 3 | -0,4 | -0,8173 | -0,4731 | -0,0946 |
| 4 | -0,2 | -0,9119 | -0,21762 | -0,0435 |
| 5 | 0 | -0,9554 |
|
|
Приложение Б
Решение домашней работы
| I | x | y | y` | dy |
| 0 | 1 | 0,0000 | 2,0000 | 0,4000 |
| 1 | 1,2 | 0,4000 | 3,2000 | 0,6400 |
| 2 | 1,4 | 1,0400 | 4,8800 | 0,9760 |
| 3 | 1,6 | 2,0160 | 7,2320 | 1,4464 |
| 4 | 1,8 | 3,4624 | 10,5248 | 2,1050 |
| 5 | 2 | 5,5674 |
|
|
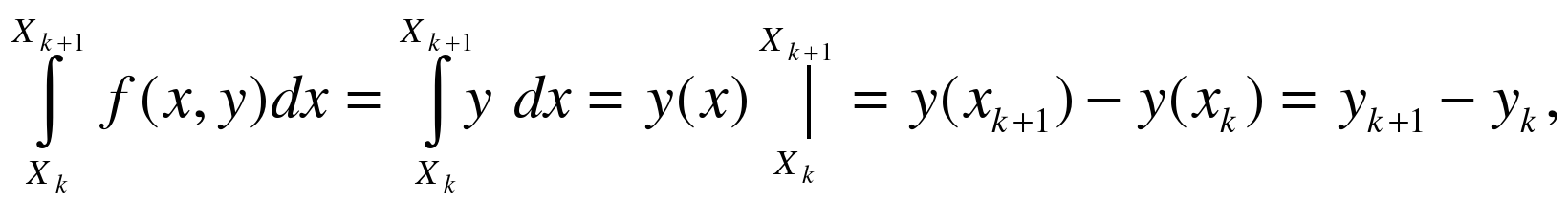
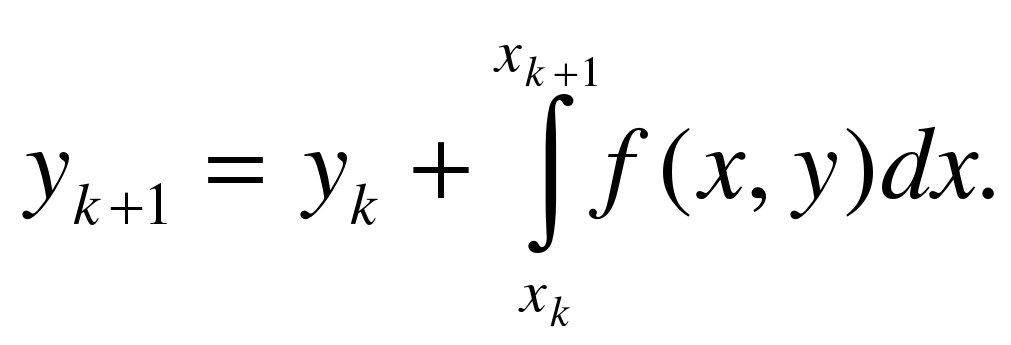 (1)
(1)





































