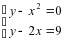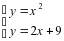| Проводится одновременно с работой учеников на компьютерах синхронно с учителем (так как скорость работы у учащихся различна, то на этом уроке целесообразно воспользоваться помощью консультантов из числа наиболее продвинутых учеников) Учитель: очень важна и нужна программа MS-Excel и при изучении математики, а именно алгебры. Кто из вас не сталкивался со сложностями при решении уравнений, систем уравнений. И вот сегодня мы займемся именно этим.
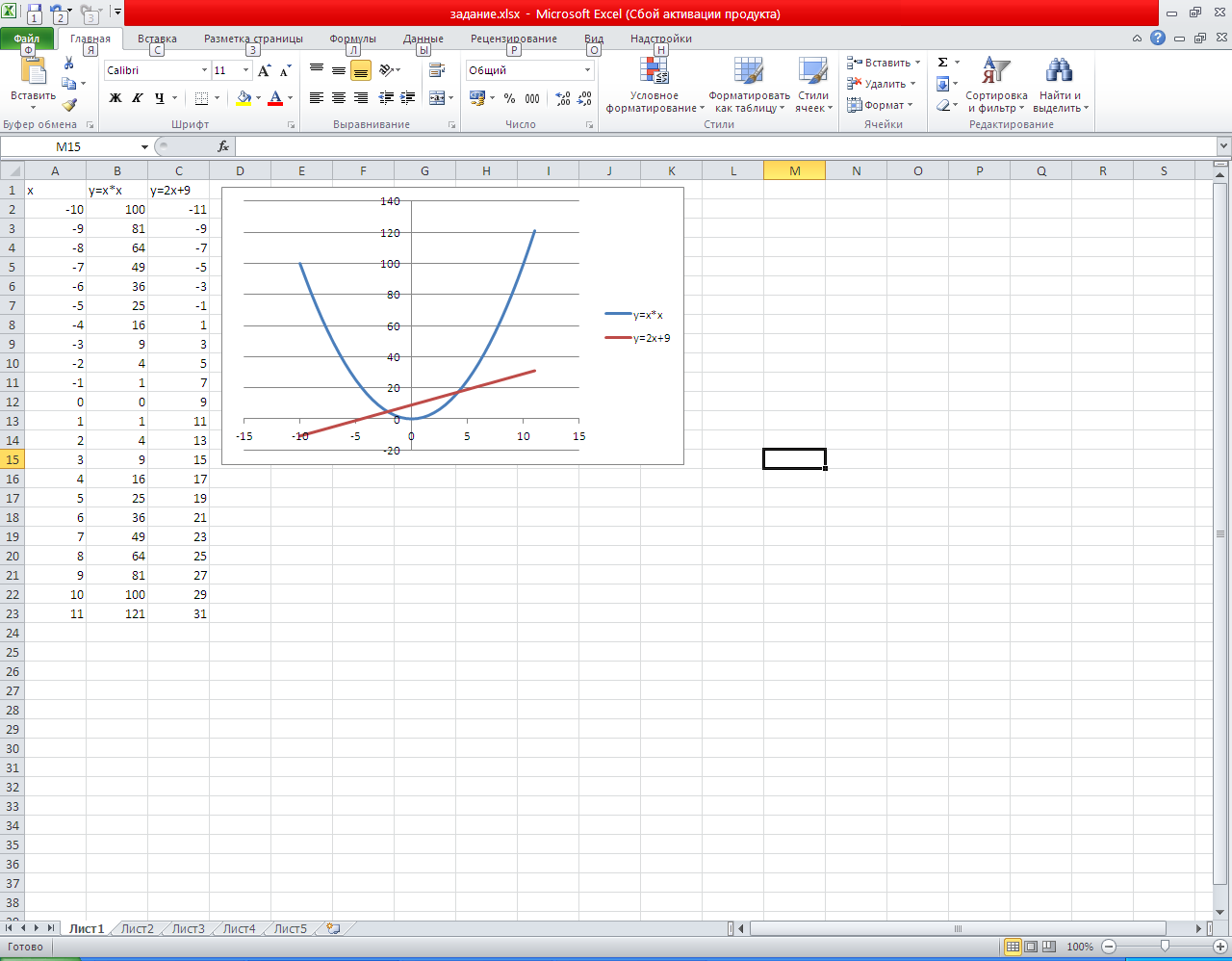
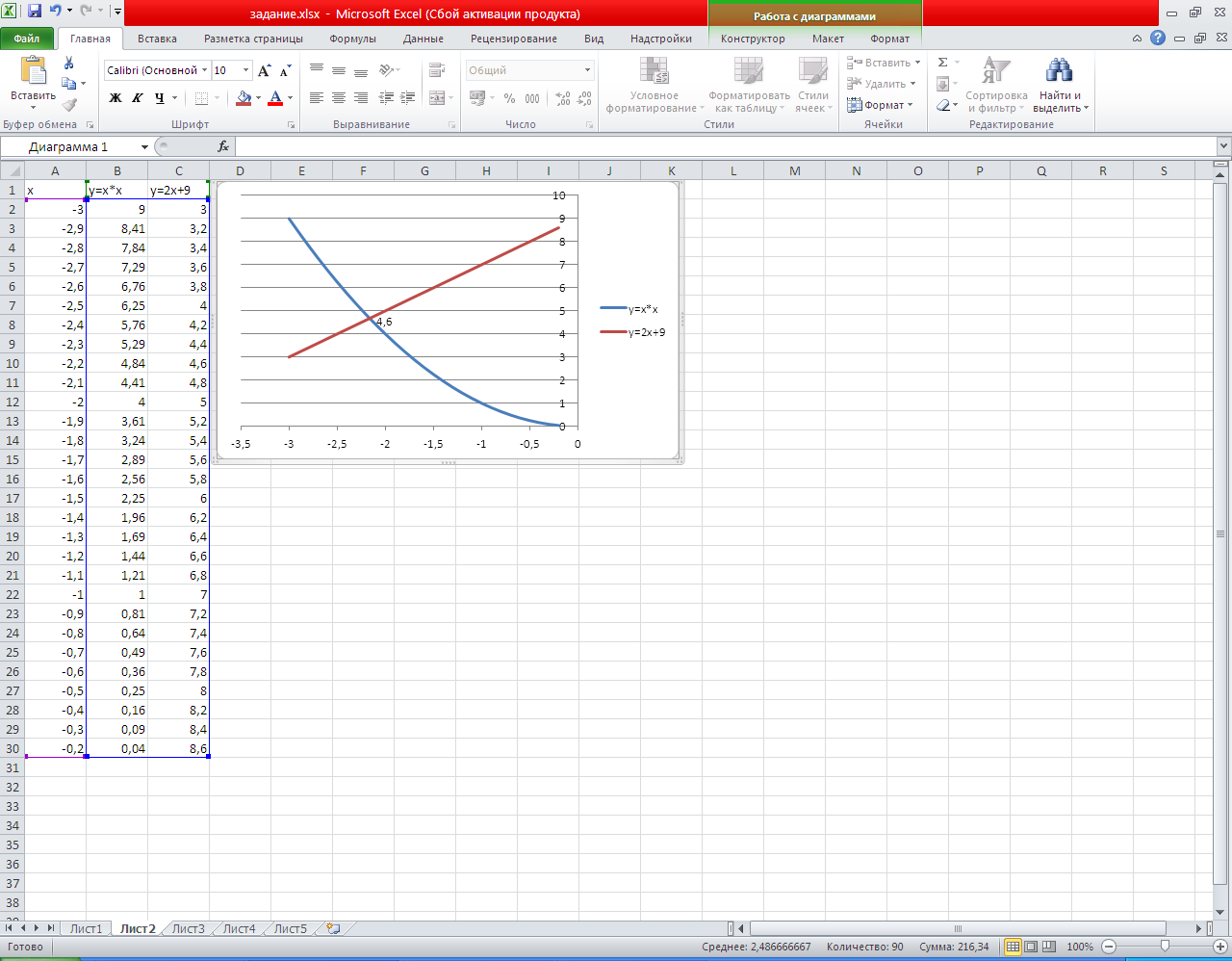
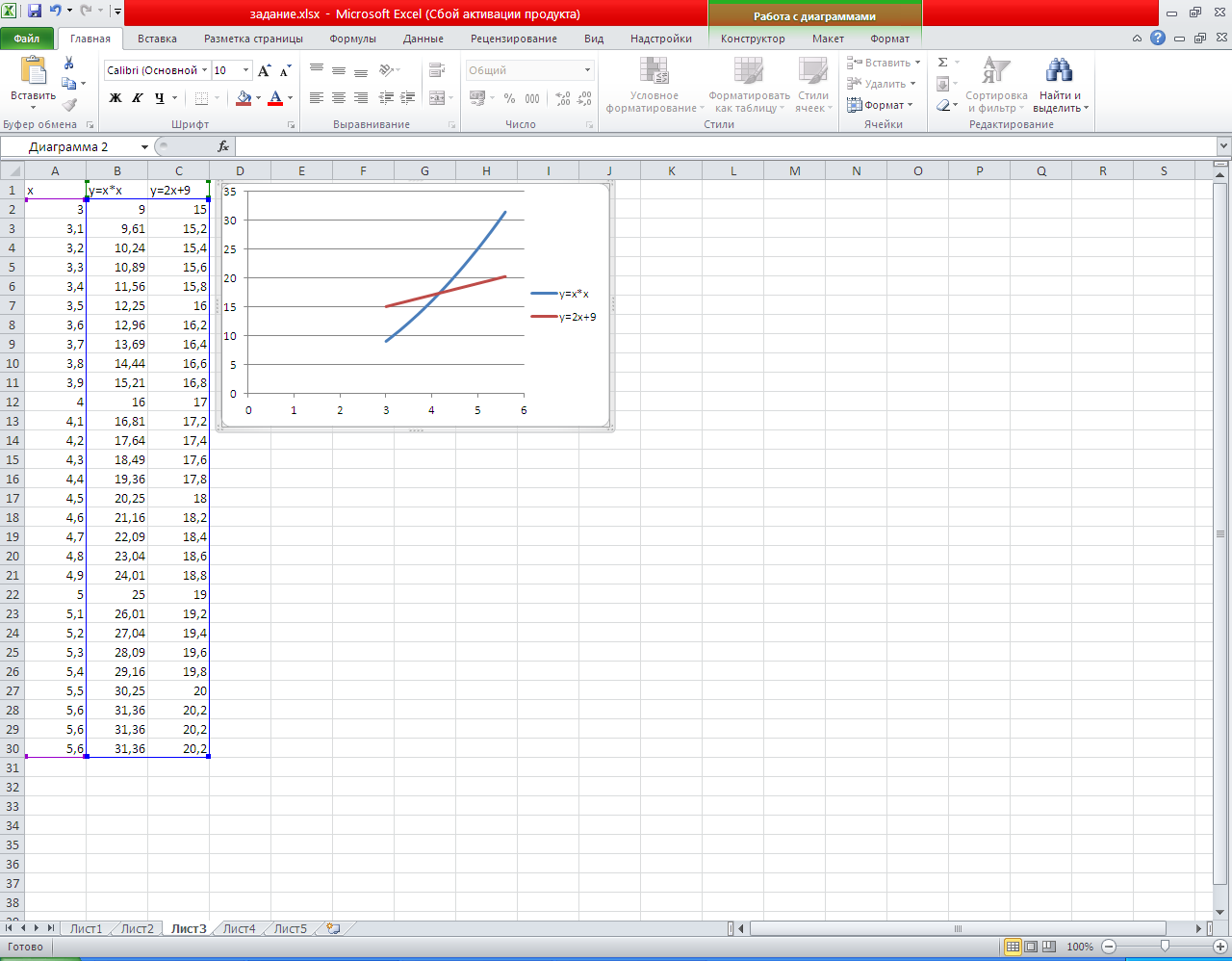
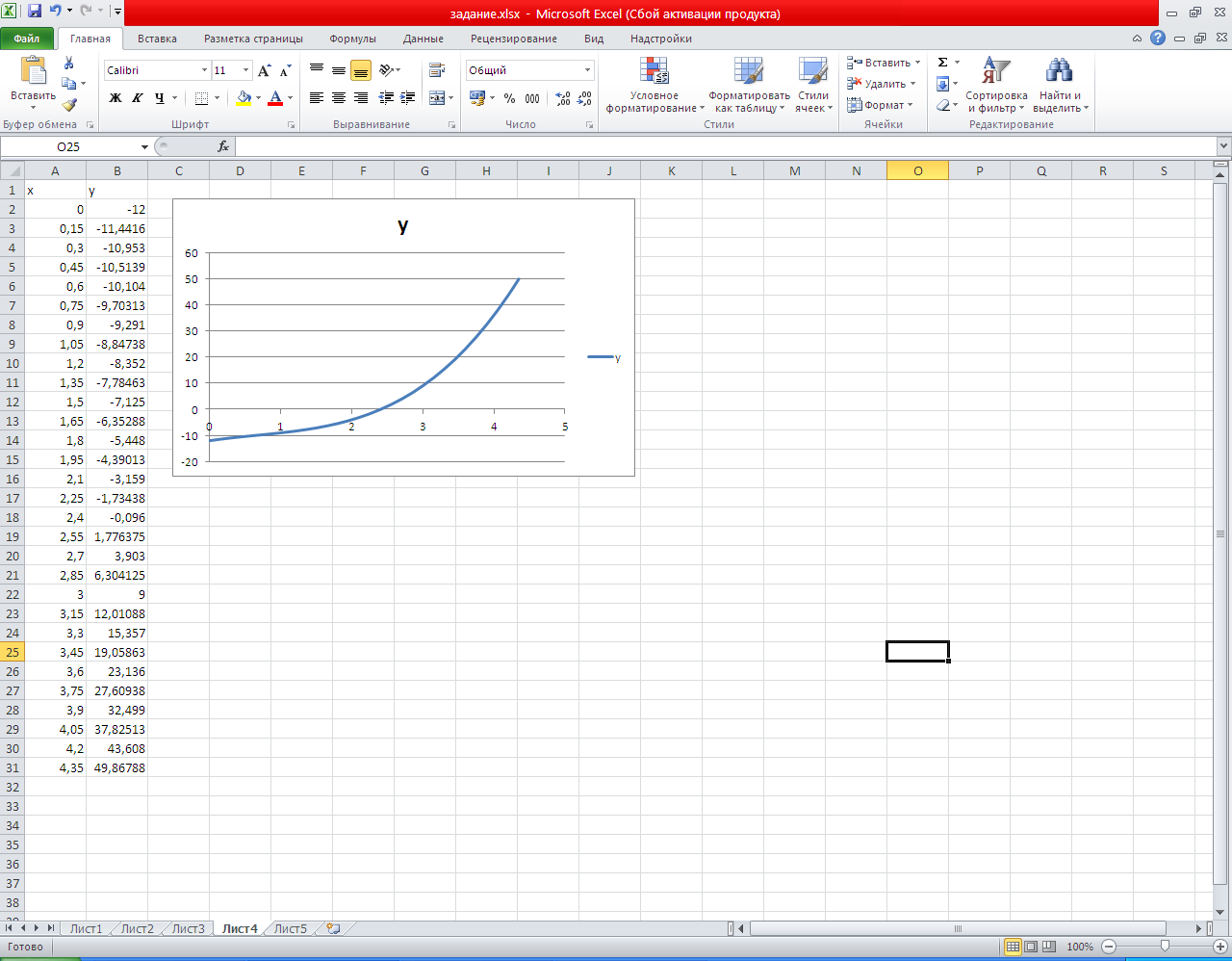
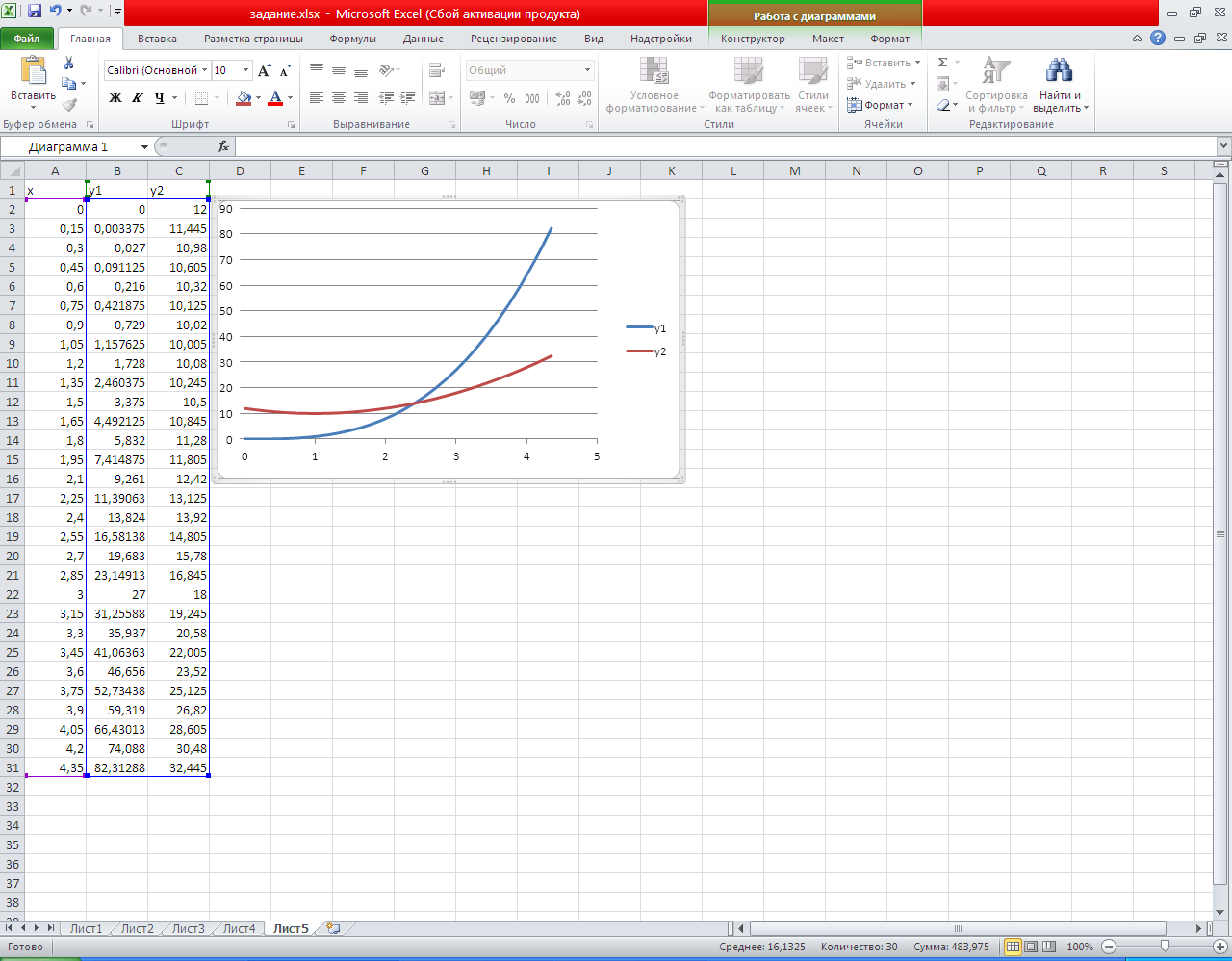
Тема урока «Применение табличного процессора Excel для графического решения уравнений n-ой степени». Из курса математики нам известно, что корнями уравнения являются значения точек пересечения графика функции (то есть нашего уравнения) с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями будут координаты точек пересечения графиков функций. Этот метод нахождения корней называется графическим. Но на прошлом занятии мы узнали, что с помощью программы Excel можно строить практически любые графики. Воспользуемся этими знаниями для нахождения корней системы уравнений графическим методом. Для примера рассмотрим решение следующей системы уравнений: 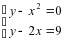 Преобразуем данную систему в приведенную: 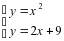 Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций. Сначала построим таблицу: • Первая строка — строка заголовков. Далее для построения этой таблицы использовались следующие формулы: при заполнении столбца А: в ячейку А2 заносится начальное значение аргумента Х=-10, для автоматического заполнения всего столбца нужно в ячейку A3 занести формулу А2+1 и скопировать ее до ячейки А23; при заполнении столбца В в ячейку В2 заносится формула А2*А2, которая затем копируется до ячейки В23; • при заполнении столбца С в ячейку С2 заносится формула 2*А2+9, и также копируется до С23. С помощью мастера диаграмм выберем тип диаграммы Точечная и построим черновую диаграмму первоначальной оценки решений. На диаграмме видно, что оба графика имеют точки пересечения — эти координаты этих точек и есть решения системы. Так как шаг изменения аргумента был достаточно велик, то мы получили приближенные значения решений. Уточним их, построив два графика в интервалах от -3 до 0, где находится первое решение, и от 3 до 5 — где находится второе. Составим новые таблицы: См. распечатки-скриншоты № 1 Для второго решения: В этом случае мы уменьшили шаг изменения аргумента для более точного построения. Решением нашей системы будут координаты точек пересечения графиков: Х1=4,2; У1=4,8; Х2=4,2; У2=17,5. Как вы уже поняли, графическое решение системы дает приблизительные результаты. С помощью диаграмм можно найти графически и решение такого уравнения: X3—2Х2+4Х—12=0. Это можно сделать, построив график и определив координаты точек его пересечения с осью ОХ, либо построив два графика: Y=X3 Y =2Х2—4Х+12 и определив точки их пересечения. Таким образом, мы видим, что используя программу Excel, можно графически решить практически любое уравнение, что мы и сделаем, получив индивидуальные задания. За правильное выполнение тренировочных упражнений учитель выдает фишки.
|