ПЛАН УРОКА №
Тема урока: Операции над высказываниями
Цели урока: Организовать деятельность учащихся по восприятию, осмыслению и первичному запоминанию новых знаний и способов деятельности. Воспитание интереса и любви к работе на компьютере.
Тип урока: - Изучение и первичное закрепление новых знаний и способов деятельности.
Наглядность: стенды, плакаты
Формы и методы: лекция-беседа
Ход урока:
- организационный момент: проверка явки учащихся на уроке, проверка наличия конспектов
- актуализация субъектного опыта учащихся: вводная беседа
Высказывание может, совпадать или не совпадать с действительностью, о которой оно что-то утверждает.
В первом случае мы называем высказывание истинным и присваиваем ему значение И, в других случаях мы называем высказывание ложным и присваиваем ему значение Л.
Из данных высказываний с помощью логических операций можно получить новые высказывания.
- проверка домашнего задания: фронтальный опрос
- Что такое высказывание
- Каким может быть высказывание
- Что изучает алгебра логики
- изучение новых знаний и способов деятельности: объяснение новой темы
Операция отрицания
Простейший случай – отрицание некоторого высказывания. Если даже высказывание а, то его отрицание обозначают символом ~ а, что читается «не а».
Маленький значок «~» служит так сказать выражением вечного духа отрицания.
Так если, а означает высказывание - «Идет дождь», то ~ а - высказывание «Дождь не идет».
Каждому высказыванию А можно сопоставить утверждение, заключающиеся в том, что высказывание А ложно. Отрицание высказывания можно обозначать и называется отрицанием А.
Рассмотрим высказывание
А≡{город Нью-Йорк – столица США}
Знак “≡” заменяет слова “есть высказывания”.
Отрицанием этого высказывания будет высказывание
≡ { Город Нью-Йорк не является столицей США}.
Заметим, что было бы ошибкой считать отрицанием высказывания А высказывание
В≡{город Вашингтон – столица США}.
Отрицание и все остальные логические операции о которых будет говорится ниже, можно пояснить с помощью простой геометрической модели.
Пусть круг на рисунке 1 обозначает высказывание А; тогда отрицанием этого высказывания соответствует остальная площадь четырехугольника, т.е. все то, что не относится к А.
Рис.1.
А
И
Л
Л
И
Если теперь высказывание А истинно (И), то , т.е. отрицание А – ложно (Л) и наоборот: – истинно, если А ложно.
Приведенная таблица называется таблицей истинности отрицания.
- обобщение и систематизация: закрепление нового материала путем ответов учащихся на вопросы
- Каким может быть высказывание
- Что такое отрицание высказывания
- Каким символом обозначается отрицание
- Графическое изображение отрицание
- В каких случаях истинно отрицание
- домашнее задание: выучить конспект, составленный на уроке
- подведение итогов занятий
- рефлексия: осознание опыта учащихся
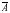и называется отрицанием А.
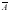≡ { Город Нью-Йорк не является столицей США}.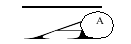
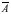
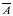, т.е. отрицание А – ложно (Л) и наоборот: 
