Автор: Лузгина Наталия Геннадьевна, учитель информатики I кв.категории МБОУ «СОШ №11» г.Балахна Нижегородской обл.
Урок на тему «Количество информации в сообщении о неравновероятном событии.
Формула Шеннона».
(10 класс, профильный уровень, по учебнику Н.Д.Угриновича)
Цель урока:
Ввести формулу для определения количества информации для неравновероятных событий.
Задачи:
образовательная: познакомить учащихся с формулой для вычисления количества информации в сообщении о неравновероятном событии, формулой Шеннона; определить качественную связь между вероятностью события и количеством информации в сообщении об этом событии; научить решать задачи с использованием формулы Шеннона.
развивающая: способствовать развитию логического мышления (умения сравнивать, делать выводы), познавательной активности.
воспитывающая: прививать навыки самостоятельной работы, работы в парах; воспитывать умение высказывать личное мнение и прислушиваться к мнению других.
Используемые технологии: проблемного обучения.
Оборудование: интерактивная доска, проектор, презентация к уроку.
Ход урока
I. Постановка цели урока.
СЛАЙД 1. Учащимся предлагается устно решить задачу:
Задача: Какое сообщение содержит большее количество информации?
В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.: 3 бит.)
Вася получил за экзамен оценку 4 (по 5-бальной системе единицы не ставят). (Отв.: 2 бит.)
Бабушка испекла 12 пирожков с капустой, 12 пирожков с повидлом. Маша съела один пирожок. (Отв.: 1 бит.)
Бабушка испекла 8 пирожков с капустой, 24 пирожка с повидлом. Маша съела один пирожок.
(В четвертом варианте учащиеся сталкиваются с ситуацией, когда события не равновероятны).
Действительно, далеко не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или "правило бутерброда".
СЛАЙД 2. Как вы думаете, какова же тема сегодняшнего урока? А цель?( исходя из выше обозначенной проблемы учащиеся сами формулируют тему и цель урока)
Ребята, вы абсолютно правы, сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.
II. Объяснение нового материала.
СЛАЙД 3. Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу:
I=log2(1/p), где
I – это количество информации,
р – вероятность события.
Вероятность события выражается в долях единицы и вычисляется по формуле:
р=K/N, где
К – величина, показывающая сколько раз произошло интересующее нас событие,
N – общее число возможных исходов какого-то процесса.
СЛАЙД 4. Вернемся к нашей задаче.
Пусть:
К1 – это количество пирожков с повидлом, К1=24
К2 – количество пирожков с капустой, К2=8
N – общее количество пирожков, N = К1 +К2, N=24+8=32
Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.
Вероятность выбора пирожка с повидлом: р1=24/32=3/4=0,75.
Вероятность выбора пирожка с капустой: р2=8/32=1/4=0,25.
Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.
Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом:
I1=log2(1/p1), I1= log2(1/0,75)= log21,3=1,15470 бит.
Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой:
I2=log2(1/p2), I2= log2(1/0,25)= log24=2 бит.
При сравнении результатов вычислений получается следующая ситуация:
вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?
СЛАЙД 5. Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик Клод Элвуд Шеннон.
Если I-количество информации,
N-количество возможных событий,
рi - вероятности отдельных событий, где i принимает значения от 1 до N, то количество информации для событий с различными вероятностями можно определить по формуле:
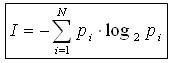
СЛАЙД 6. можно расписать формулу в таком виде:
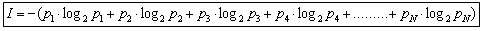
Знак минус в формуле не означает, что количество информации в сообщении – отрицательная величина. Объясняется это тем, что вероятность (р), согласно определению, 0. Т.к. Log числа, меньшего 1 (т.е. log pi) – величина отрицательная, то произведение вероятности на логарифм числа будет положительным.
Рассмотрим формулу на нашем примере:
I = - (р1∙log2p1 + р2∙log2p2),
I= - (0,25∙ log20,25+0,75∙ log20,75)≈-(0,25∙(-2)+0,75∙(-0,42))=0,815 бит
СЛАЙД 7. Теперь ответьте на вопрос задачи, которая была поставлена в начале урока: Какое сообщение содержит большее количество информации?
В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.: 3 бит.)
Вася получил за экзамен 3 балла (по 5-бальной системе единицы не ставят). (Отв.: 2 бит.)
Бабушка испекла 12 пирожков с капустой, 12 пирожков с повидлом. Маша съела один пирожок. (Отв.: 1 бит.)
Бабушка испекла 8 пирожков с капустой, 24 пирожка с повидлом. Маша съела один пирожок. (Отв.: 0,815 бит.)
Ответ: в 1 сообщении.
Обратите внимание на 3 и 4 задачу. Сравните количество информации.
Мы видим, что количество информации достигает максимального значения, если события равновероятны.
Можно ли применить формулу К. Шеннона для равновероятных событий?
Если p1=p2=..=pn=1/N, тогда формула принимает вид:
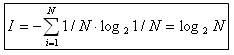
Мы видим, что формула Хартли является частным случаем формулы Шеннона.
III. Закрепление изучаемого материала.
СЛАЙД 8.
Задача №1: (объясняет учитель)
В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.
Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?
Дано: Кк=4;N=32
Найти: Iк, I
Решение:
Найдем количество клубков черной шерсти:
Кч=N- Кк; Кч=32-4=28
Найдем вероятность доставания клубка каждого вида:
pк= Кк/N, pк =4/32=1/8;
pч= Кч/N, pч =28/32=7/8;
Найдем количество информации, которое несет сообщение, что достали клубок красной шерсти:
Iк= log2(1/(1/ pк)), Iк = log2(1/1/8)= log28=3 бита
Найдем количество информации, которое несет сообщение, что достали клубок шерсти любой окраски:
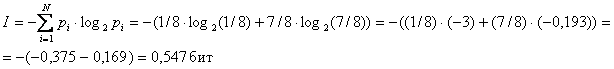
Ответ: Iк=3 бит; I=0,547 бит
(Задачи 2-4 учащиеся решают в парах с дальнейшей защитой решения у доски).
Задача №2: В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?
Задача №3: В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?
Задача №4: В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.
VI. Подведение итогов урока.
СЛАЙД 9. Ответьте на вопросы:
Объясните на конкретных примерах отличие равновероятного события от неравновероятного?
С помощью какой формулы вычисляется вероятность события?
Объясните качественную связь между вероятностью события и количеством информации в сообщении об этом событии?
В каких случаях применяется формула Шеннона для измерения количества информации?
В каком случае количество информации о событии достигает максимального значения?
V. Домашнее задание.
СЛАЙД 10. §2.4 стр.111-113. Устно №2.3 стр.114-115. Письменно №2.3 стр.115
ИСТОЧНИКИ:
Н.Д.Угринович «Информатика и ИКТ». Учебник для10 класса, профильный уровень.
http://marknet.narod.ru/spr/list5.htm Информатика. Справочный материал. Количество информации. Формулы Хартли и Шеннона
Н.Д.Угринович, методическое пособие «Информатика и ИКТ 8 -11 класс»
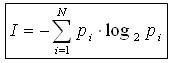
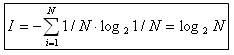
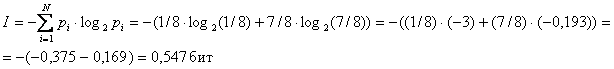



 I 1 = log 2 (1/0 , 75) = log 2 1 ,3 = 1,15470 бит К-во информации в сообщении, что Маша выбрала пирожок с капустой: I 2 = log 2 (1/p 2 ) = I 2 = log 2 (1/0 ,2 5) = log 2 4 = 2 бита =1 Чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии Company Logo" width="640"
I 1 = log 2 (1/0 , 75) = log 2 1 ,3 = 1,15470 бит К-во информации в сообщении, что Маша выбрала пирожок с капустой: I 2 = log 2 (1/p 2 ) = I 2 = log 2 (1/0 ,2 5) = log 2 4 = 2 бита =1 Чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии Company Logo" width="640"






















