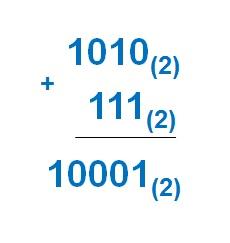Урок по теме "Арифметические операции в позиционных системах счисления" в 9 классе. На уроке применяется смешанная система работы включающая работу с интерактивными рабочими листами (ИРЛ) создаными в google диске. Примеры ИРЛ данны в виде ссылок и доступны для копирования. Использование ИРЛ позволяет совершенствовать ИКТ-компитентность учеников и улучшают наглядность материала. Для использования ИРЛ желательно (но не обюязательно) регистрация вакаунта в google. Также данный урок можно использовать на уроках по ФГОС.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
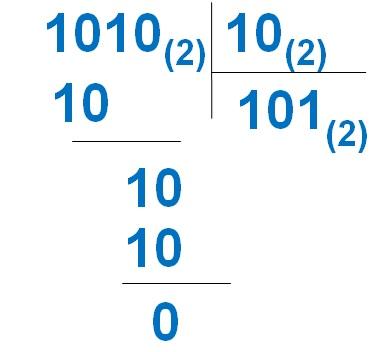
Арифметические операции в позиционных системах счисления с использованием интерактивных рабочих листов
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Арифметические операции в позиционных системах счисления с использованием интерактивных рабочих листов »
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
2720 руб.
1670 руб.
2380 руб.
1860 руб.
2660 руб.
1860 руб.
2660 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства