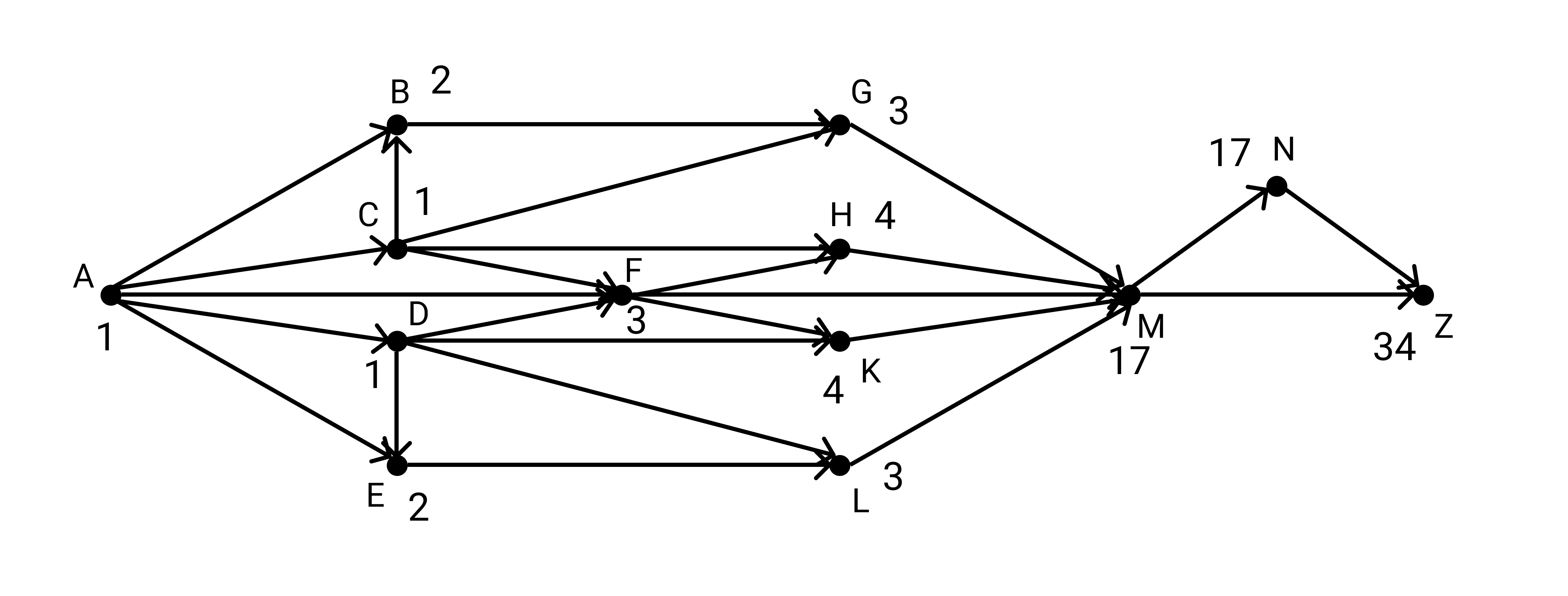
Разработка задание ЕГЭ по теме: "Поиск путей в графе".

Поиск путей в графе.

В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). То есть ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка, - потомком.

Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.

Подсчет путей в ориентированном графе

На рисунке — схема дорог, связывающих города А, Б,В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение

Каждой вершине, начиная с начальной (А), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины А (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом — никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один — вершина А).

У вершины Д предками являются А и Б, значит, индекс вершины Д равен 1+1 = 2.

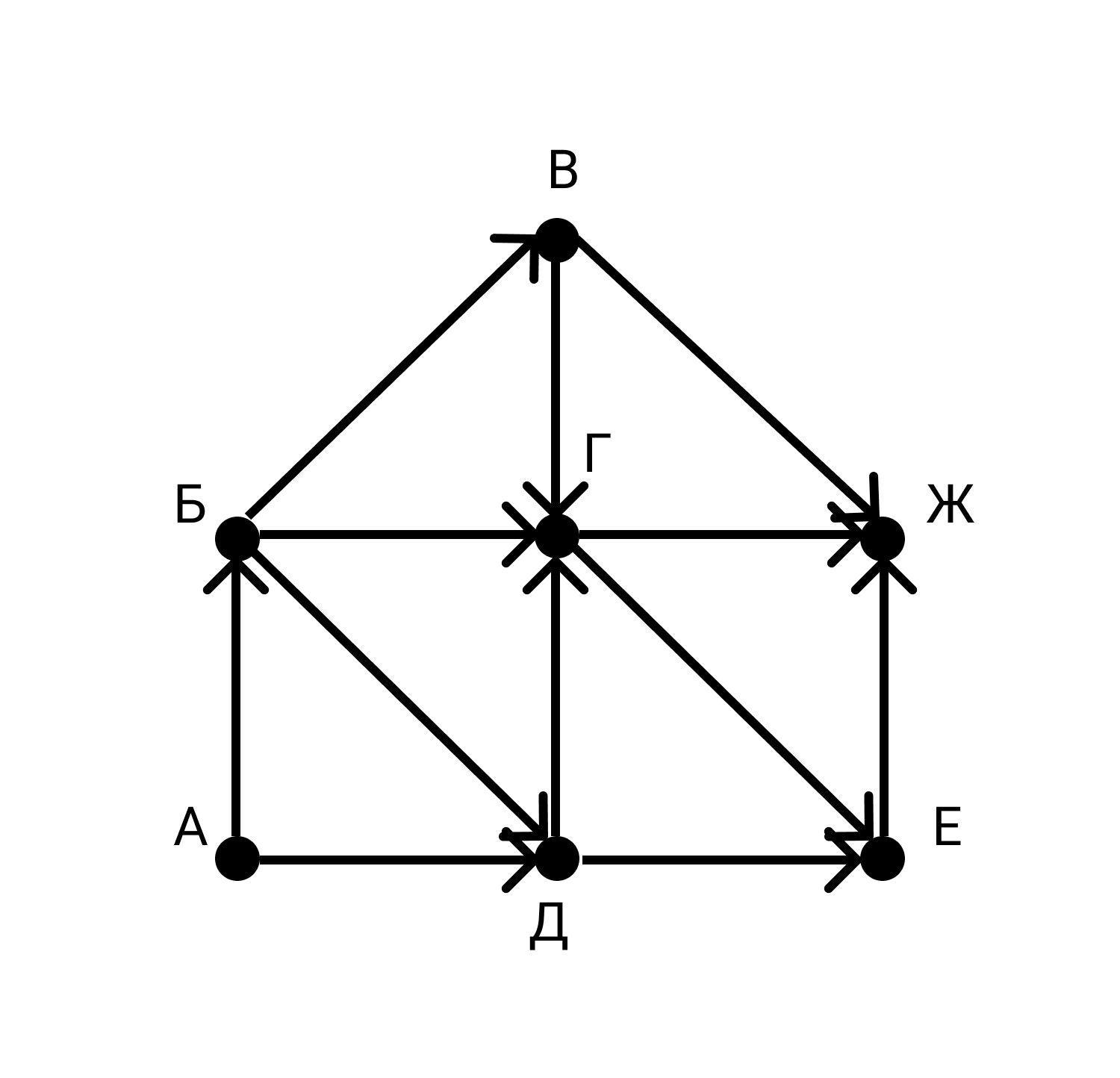
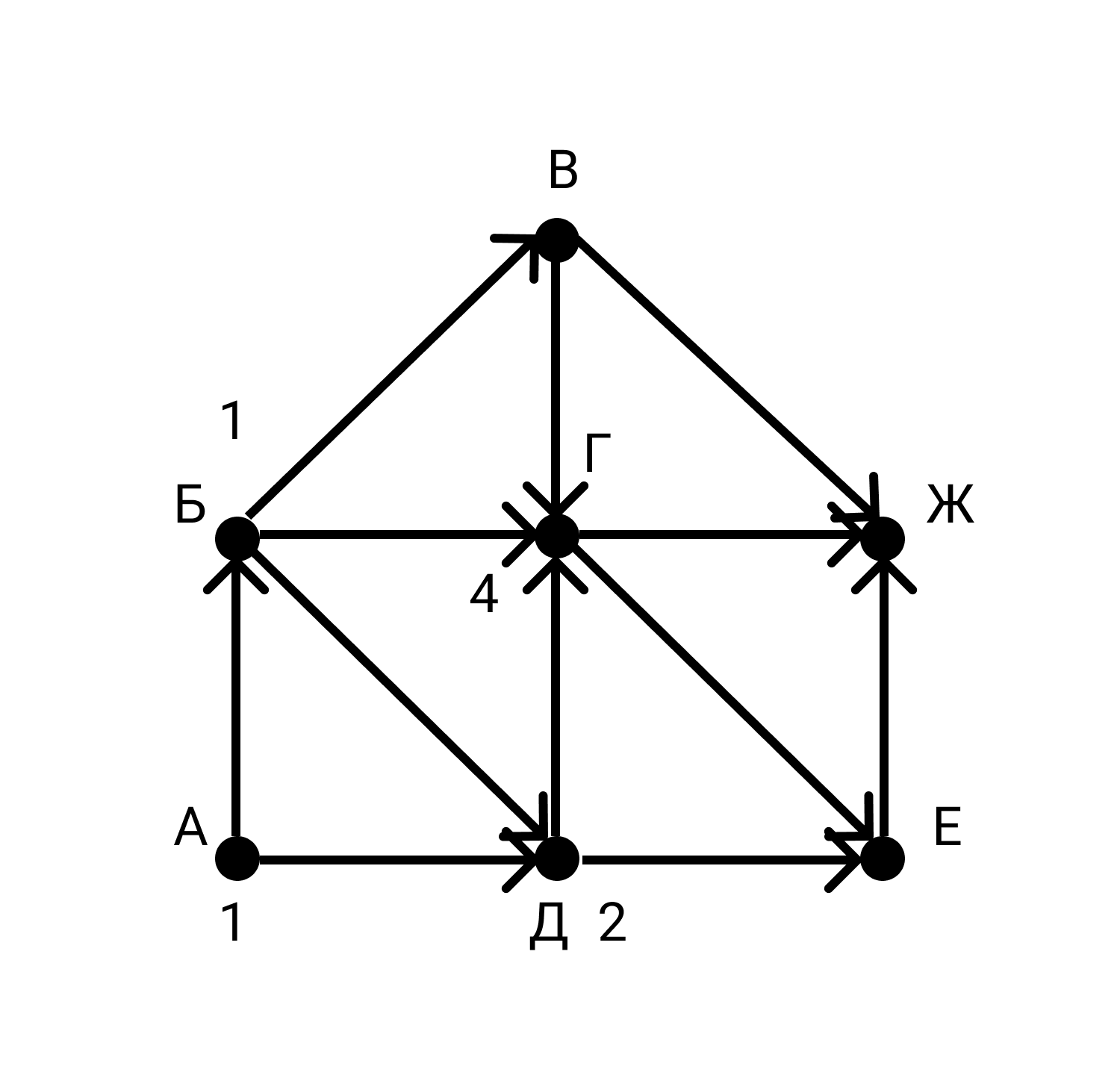
Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин. Индекс вершины Ж и будет ответом задачи.

Ответ: 11.

На рисунке — схема дорог, связывающих города A, B, C, D, E, F, G, H, G, K, L, M, N, Z. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Z?

Решение

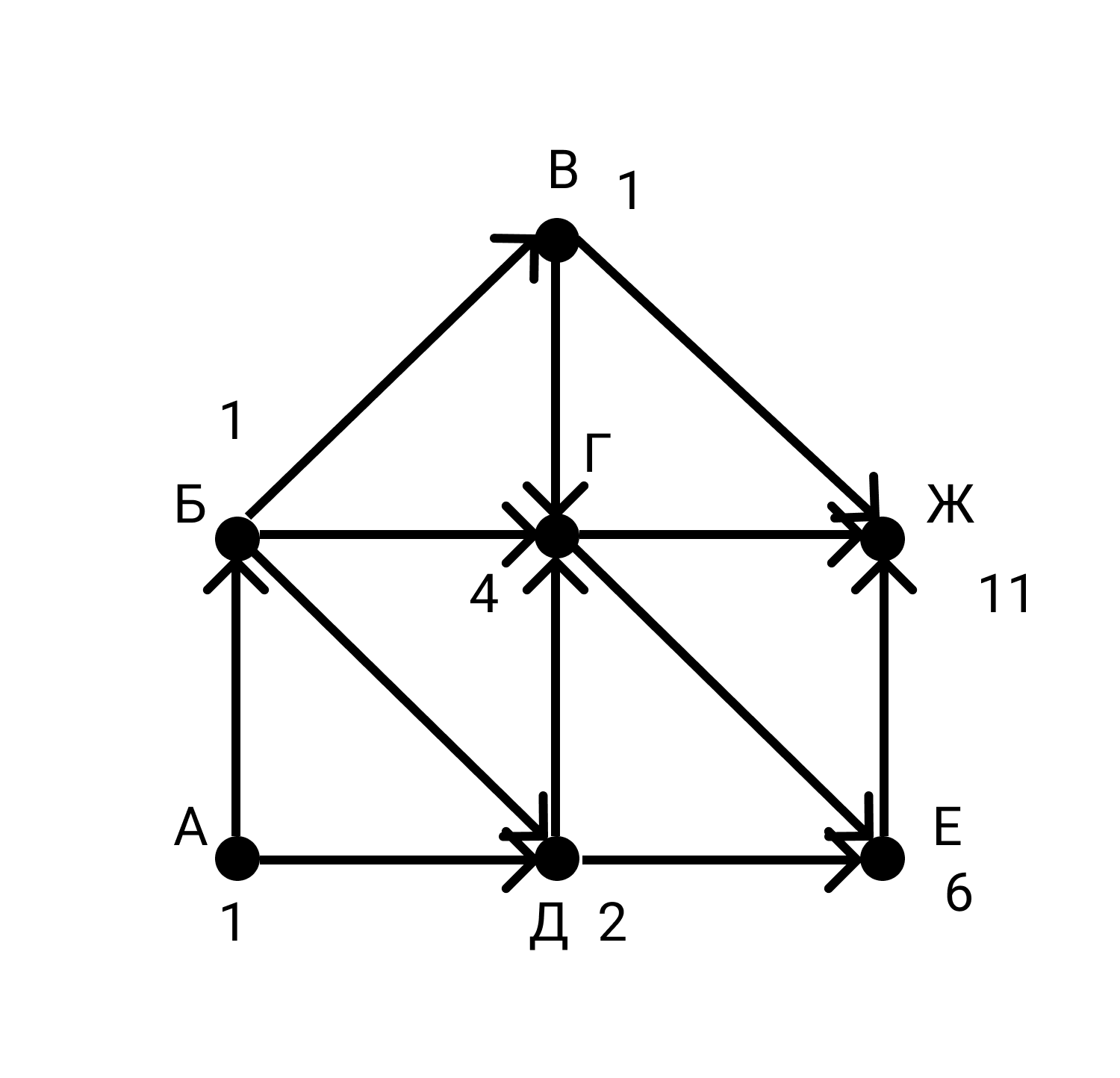
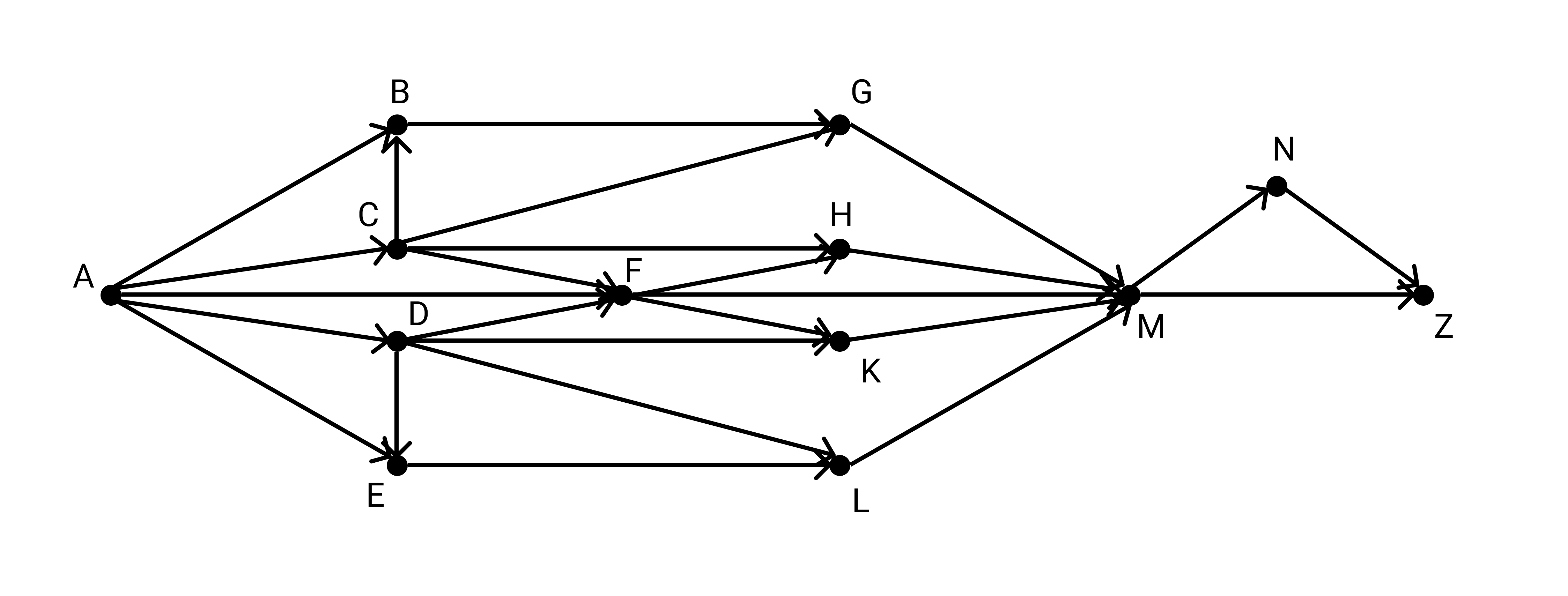
Задача решается абсолютно так же, как предыдущая. Присваиваем начальной вершине

А индекс 1 и последовательно считаем индексы всех вершин до Z:

Ответ: 34.