Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Обобщение педагогического опыта по теме «Реализация компетентностного подхода, как условие развития латерального мышления учащихся на уроках ИКТ»
Просмотр содержимого документа
«Обобщение педагогического опыта»
«Реализация компетентностного подхода, как условие развития латерального мышления учащихся на уроках ИКТ»
Егоров Сергей Иванович
учитель информатики и ИКТ
ГКОУ Кадетской школы - интената
«Кадетский корпус»
им. Д. М. Пожарского
2015 год г. Радужный
Наименование опыта
Реализация компетентностного подхода, как условие развития латерального мышления учащихся на уроках ИКТ.
Условия возникновения опыта
Сегодня стратегия развития России до 2020 г., предложенная Правительством страны, показывает, что радикальные реформы, характерные для настоящего времени, могут и должны перерасти в реформаторские процессы, определяющие жизнь общества на много лет вперед.
В этом ключе задача школы состоит в создании условий для воспитания поколения с незашоренным мышлением, способным к его свободному проявлению. Система образования может рассматриваться как ресурс подготовки специалистов будущего, способных нестандартно решать поставленные перед ними задачи и воспринимать любые новые технологии.
Это достижимо, но только не современными стандартизованными методами. К сожалению, нас захлестнула стандартизация. Школам «спускают» типовые программы, дидактические единицы, тесты и прочее практически по всем дисциплинам.
Стандартизация – вещь необходимая и полезная там, где присутствуют постоянно повторяющиеся действия, рутинные процедуры. В подготовке специалистов, готовых к восприятию новейших технологий в любых отраслях научной, экономической и общественной жизни стандартизация может стать тормозом.
На уроках информатики и ИКТ, особенно при изучении алгоритмизации и программирования, можно реализовать компетентностный подход как условие развития нестандартного мышления учащихся. Этой темой я начал заниматься ещё в 90-х годах, работая в школе №1 города Радужного, а с 2005 года перенёс этот опыт в ГООУ Кадетскую школу-интернат «Кадетский корпус» им. Д.М. Пожарского.
Актуальность и перспективность опыта
Система образования в нашей стране вступает в период фундаментальных перемен, характеризующихся новым пониманием целей и ценностей образования, осознанием необходимости перехода к непрерывному образованию, новым подходам к разработке и использованию технологий обучения.
Одна из главных задач школы состоит в том, чтобы не только дать знания учащимся, но и пробудить личностный мотив, привить интерес к обучению, тягу к саморазвитию, "научить учащихся учиться" посредством совершенствования мыслительного процесса.
Несмотря на то, что изучению особенностей мыслительного процесса человека посвящено большое количество исследований (Фрейд З., Веккер Л., Рубинштейн С., Тихомиров О.), на сегодняшний день особенно востребованными являются методические разработки и рекомендации, ориентированные на оказание помощи педагогу в развитии нестандартного, креативного мышления, способного реализовать компетентностную стратегию развития образования. Суть востребованности данных разработок в необходимости подготовить ученика к деятельности в нестандартных, нетрадиционных условиях.
Ведущая педагогическая идея
Педагогическая идея состоит в том, что в настоящих условиях развития современного образования педагогу важно помочь учащемуся научиться действовать не только используя стереотипные мыслительные операции (действие по шаблону, инструкции, алгоритму), но и разработать индивидуальные стратегии организации мыслительных процессов. Это должно отразиться в индивидуальных стратегиях мышления учащихся в условиях организации учебного процесса.
Сегодня крайне востребован переход от передачи учащимся «готовых» знаний к воспитанию потребности в поиске логических связей в предъявляемой информации и индивидуальной ее обработке. Информация тогда может стать личностно значимой, а полученные знания учениками будут систематизированы, когда в процессе диалога с учителем, с компьютерной программой, с самим собой у него будет формироваться индивидуальный путь восприятия, обработки и использования полученной информации, что возможно при условии развития индивидуальных стратегиях мышления учащихся.
Теоретическая основа опыта
Опираясь на формулировку педагогической идеи настоящего опыта, мы принимаем за основу воспитание у учащихся нестандартного или латерального мышления.
Понятие "латеральное мышление" ввел в научный обиход доктор Эдвард де Боно. Латеральное мышление занимается исследованием всех возможностей, прибегая к перегруппировке и перестроению доступной информации.
Само значение слова "латеральное" означает движение в сторону - для нахождения альтернативных решений, - вместо того чтобы, развивая какую-то отдельную модель, двигаться прямолинейно. Это такой своеобразный "ход конем".
Задача мышления вообще - собирать информацию и использовать ее как можно лучше. Существует два типа мышления: логическое и латеральное, которые дополняют друг друга. Вся система классического образования построена на логическом мышлении. Логическое мышление подвергает концептуальные модели проверке, проверяя их действенность. Латеральное мышление связано с перестройкой таких моделей (интуиция) и созданием условий для построения новых моделей (творчество).
Существуют несколько методов обучения нестандартному логическому мышлению – метод ассоциаций, метод проекций, и так далее.
Ассоциация - это связь между отдельными представлениями, при которой одно из представлений вызывает другое. Как бы перекидываются мостики между решаемой задачей и сходными признаками или свойствами другого объекта. Этим другим объектом может быть что угодно: системы из живой и неживой природы, сказочные герои, любое воспоминание, образ или символ, даже запах или звук. Если аналогия - это сходство, анализ - это расчленение, то ассоциация - это связывание каких-либо свойств, качеств, может быть, и очень далеких. Цели ассоциативного мышления (творческого синтеза): создание новых оригинальных идей, создание смысловых связей, стимуляция воображения, улучшение запоминания и вспоминания. Различают следующие виды ассоциаций (по Аристотелю):
По смежности, то есть по близости, по соседству в пространстве или во времени, когда одно представление вызывает в сознании другое благодаря их временному или пространственному совпадению. Например: улей - пчелы, медведь - зима - берлога, зима - мороз - снег...
По сходству, по подобию, то есть похожее по какому-то признаку: по форме, по цвету, по восприятию, по функции... Например: мяч - арбуз, лимон - лимонад, снег - вата...
По контрасту, то есть противоположное по каким-то свойствам. Например: добро - зло, гора - равнина, гора - ущелье, искры - снежинки...
Проекция (по Фрэйду) - это механизм бессознательного переноса индивидом своих мыслей, переживаний, состояний, свойств, черт и т. д. на других людей. В энциклопедии, проекция - это один из защитных механизмов, состоящий в том, что неприемлемые чувства, желания и даже некоторые аспекты личности человек отчуждает от себя и приписывает кому-то другому. Я использую метод проекций в более узком смысле – это попытка представить себя на месте других людей, в другой обстановке.
Одним из основных методов, по мнению доктора Эдварда де Боно, является поиск альтернатив при решении различных проблем. Он считает, что ключевым моментом латерального мышления является поиск и порождение альтернатив. Обычно, когда находят альтернативу в виде перспективного варианта, на нем и останавливаются. На самом деле, нужно отметить этот вариант и перейти к поиску следующего.
Возможны четыре варианта поиска альтернатив:
Можно сначала найти ряд альтернативных вариантов, а затем вернуться к найденному варианту.
Найденную альтернативу можно принять за отправную точку поиска новых альтернатив.
Найденная альтернатива может решить проблему, и дальнейших усилий не потребуется.
Найденная альтернатива может привести к перегруппировке имеющихся данных, и проблема будет решена опосредственно, с помощью такого обходного маневра.
Конечно, всё это применить в рамках школьной программы затруднительно, но при изучении программирования, решая задачи на компьютере, 2 – 3 альтернативных варианта можно проработать.
Необходимо также на уроках уделять внимание интуиции. Философ Сократ был уверен, что главные идеи были ему продиктованы его личным демоном Даимониумом (внутренним голосом). Мы также должны ежедневно разговаривать со своим внутренним голосом.
Интуиция, этот бесконечно драгоценный дар, который позволяет человеку подняться до уровня трансцендентальной реальности, является между тем и одной из недоразвитых способностей человека.
Человек тем безопаснее идет своим путем, чем сильнее и увереннее его интуиция. Реальность существования так называемого шестого чувства — интуиции — считается достаточно обоснованной. Большинство людей в течение всей жизни совершенно не использует возможностей этой творческой силы. А если и приходится когда-либо ею воспользоваться, то происходит это спонтанно, непреднамеренно, беспорядочно. Лишь очень ограниченное число людей применяет интуицию обдуманно и преднамеренно.
Об индивидуальных стратегиях мышления учащихся в педагогической литературе активно заявили в 80-е годы представители ТРИЗ - педагогики (Г.Альтшуллер, А. Гин, и др.). В настоящее время данная идея рассмотрена и развивается в работах А. Плигина.
Новизна опыта
«Реализация компетентностного подхода как условие развития нестандартного мышления учащихся на уроках ИКТ»– тема, над которой пытаются работать многие учителя предметники. У каждого педагога свой путь решения данной проблемы.
Решение нестандартных задач способствует развитию определенных приемов мышления.
Традиционным считается такой способ или алгоритм решения задач:
постановка задачи,
выделения исходных данных,
применение готовых изложенных законов и формул,
получение результата.
Используя настоящий алгоритм, достаточно выучить правила, формулы и обозначения, чтобы стать хорошим учеником. К сожалению, жизнь перед выпускниками не ставит готовых задач, и такой подход не позволяет адаптироваться ребенку в современном сложном мире. Поэтому формулируя задачи, в которых исключаются прямые указания на исходные данные, способы решения и ожидаемый результат, педагог выводит ученика на более высокую ступень развития, способствуя формированию базовых компетенций. Ученики выделяют необходимые данные, прогнозируют результат и в зависимости от желаемого результата выбирают способы решения. Новизна опыта заключается в применении методов Эдварда де Боно на уроках информатики и ИКТ.
Адресная направленность
Данный педагогический опыт может быть использован не только учителями информатики средних общеобразовательных школ, осваивающими новые образовательные технологии, но и другими учителями предметниками.
Использование представленного опыта может быть полезно в любых типах общеобразовательных учреждений, независимо от уровня владения учащимися теми или иными навыками в области информатики и информационных технологий.
Технология опыта
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Также мною используется на уроках метод проекций. При объяснении темы «Введение в системы счисления» учащимся трудно переломить своё сознание, что кроме 10-й системы счисления существуют множество других позиционных систем счисления (особенно, если они слышат об этом впервые). Не секрет, что одна из причин использования всем человечеством, как основной, 10-й системы счисления, заключается в том, что у каждого человека на двух руках – десять пальцев. Удобнее было древним людям подсчитывать добычу в 10-й системе счисления. Я предлагаю учащимся представить себя на какой-нибудь планете во времена каменного века, но у всех у них на двух руках по семь пальцев. Как бы они подсчитывали добычу в позиционной системе счисления, используя только то, что им дала природа. Понимание многообразия позиционных систем счисления приходит гораздо быстрее.
Но как я уже говорил, одним из основных методов, по мнению доктора Эдварда де Боно, является поиск альтернатив при решении различных проблем. Решение нестандартных задач посредством поиска альтернатив способствует развитию определенных приемов мышления. Поэтому, на мой взгляд, важно начинать многие уроки с примеров из жизни о проявлении нестандартного логического мышления, так как даже «бытовые» примеры воспринимаются учащимися легче, чем незнакомые научные термины. Именно таким образом организован у меня урок «Введение в алгоритмизацию и программирование».
Тема урока : Введение в алгоритмизацию и программирование ( 9-й класс ).
Цель урока : Создание условий для реализации компетентостного подхода как условия развития нестандартного мышления учащихся.
Форма урока: Комбинированный урок, с использованием компьютерной техники для демонстрации наглядных примеров.
Вступление :
Решая многочисленные задачи в нашей повседневной жизни, мы привыкли выполнять их традиционно – «как учили», то есть, опираясь на свои знания и опыт. К сожалению, у нас в средней школе, мне кажется, по многим предметам обучение предполагает именно такой подход. Например, да простят меня учителя математики, - умножение столбиком. Хотя, существуют и другие способы умножения чисел.
Тезисы урока.
Рассказ о небоскрёбе в Америке. Возникла проблема у жильцов этого дома, связанная с одним лифтом, пусть и скоростным, но при полном заселении небоскрёба лифта приходилось очень долго ждать. Нужно было в короткие сроки и с минимальными затратами решить эту задачу. Специалисты, каждый в своей области, предлагали стандартные решения, «как их учили». Но ни одно из них не было быстрым и требовало значительных затрат. И когда все зашли в тупик, один предложил решение, совершенно абсурдное, с точки зрения специалистов – технарей. Он предложил на каждом этаже около лифта развесить зеркала в полный рост. Но как оказалось, он предложил дешёвое и красивое решение проблемы, обратившись к решению задачи с совершенно неожиданной стороны, проявив при этом нестандартное логическое мышление, так как жалобы со стороны жильцов сразу прекратились.
При составлении алгоритмов ( программ ) не существует формул и догм, по которым они должны составляться. Можно также зайти с неожиданной стороны и решить поставленную задачу, проявив при этом нестандартное мышление и творческие способности. Примером может служить простая задача, которую проходят по математике в 7-м классе, - нахождение НОД двух чисел. Кратко : нужно разложить оба числа на простые множители ( при этом необходимо знать все простые числа до определённого N ), найти общие множители в обоих разложениях и их перемножить. А вот за 4000 лет до нас Евклид предложил простой в понимании и очень элегантный алгоритм, который вошёл в историю, как «Алгоритм Евклида». При переложении на язык программирования, он выражается в четыре оператора! Очень даже красиво.
На районной олимпиаде 2003 года была предложена следующая задача: Необходимо случайно задать координаты 100 точек на графическом экране, затем соединить их отрезками прямых линий слева – направо. Для проверки комиссии было дано решение этой задачи математическим способом с сортировками координат всех точек. Получалось достаточно громоздкое решение. Один мой ученик предложил постое решение: рассыпать точки по экрану и сканируя их слева – направо, сразу соединять их отрезками. Простое, элегантное решение. Два разных подхода – результат один – решение поставленной задачи.
Показ простых линейных алгоритмов: нахождение числа А в некоторой степени за определённое количество умножений. Большинство таких задач решаются традиционно, по шаблону. Но есть случаи, когда шаблон не срабатывает. Нужно начать всё сначала, и проявить при этом нестандартный подход ( немного не так «как учили» ). Это простейшая демонстрация проявления нестандартного логического мышления.
Анализ урока:
Урок проходит в режиме активного диалога учитель – воспитанники. Наиболее реальный путь формирования мотивации - это обращение к действительно интересным для детей проблемам, создание условий самореализации и самоутверждения в близкой им среде. Знания, приобретенные в школе, только тогда становятся значимыми, когда воплощаются в реальной жизни. И лишь тогда урок становится интересным, когда именно в школе находятся ответы на вопросы, возникающие в социально-бытовом окружении.
Активный диалог предусматривает и творческий подход учителя, потому что каждый раз учащиеся предлагают свои пути решения тех или иных проблем. Получается, что учитель также находится в роли обучаемого, совершенствуя раз от разу этот конкретный урок. Вторая часть урока – наглядная демонстрация конкретных алгоритмов, и переход к самостоятельному решению простых линейных алгоритмов с использованием языка Паскаль, где поняв постановку задачи, учащиеся активно пытаются решить её не совсем стандартным способом, проявляя при этом живой интерес. В результате у большинства воспитанников пересматриваются взгляды на программирование, которое раньше им казалось «китайской грамотой», и после этого многие из них проявляют живой интерес к программированию, как к инструменту, где, как мне кажется, раскрываются их творческие способности.
Результативность
При объяснении темы «Линейное программирование» в качестве примера приводится следующая задача:
«Дано число А. Не пользуясь никакими арифметическими операциями, кроме умножения, требуется найти А в 21-й степени за 6 операций умножения».
Составляется алгоритм выполнения этой задачи, который подходит для решения большинства подобных заданий. Смысл состоит в удвоении степени на начальных шагах алгоритма. Дальше решение очевидно. Но из этого класса есть некоторые задачи, в которых чтобы добиться результата нужно начинать не так, как в основной массе.
Одному классу я сразу даю эти задачи, а у другого сначала рассказываю о нестандартном логическом мышлении с житейскими примерами и с поиском альтернатив. В результате воспитанники прослушавшие лекцию о латеральном мышлении быстрее находят нестандартное решение.
|
| 2011/2012 | 2012/2013 | 2013/2014 | ||||||
| Кол-во учащихся | Справились | % | Кол-во учащихся | Справились | % | Кол-во учащихся | Справились | % | |
| Без лекции | 18 | 2 | 11% | 21 | 0 | 0% | 23 | 1 | 4% |
| С лекцией | 20 | 11 | 55% | 19 | 9 | 47% | 21 | 12 | 57% |
Приложения
Наибольший общий делитель
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел - это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12, 18) = 6.
Факторизация - разложение данного натурального числа на простые множители.) приводит к следующему программному коду: (взято на форуме программистов)
var
powers: array[1 .. 10000] of longint;
a,b:text;
h,next_number:longint;
arr:array[1..20] of longint;
procedure Factorization(x: longint);
var i: longint;
function DivX: word;
var count: word;
begin
count := 0;
while (x 1) and (x mod i = 0) do begin
inc(count);
x:= x div i;
end;
DivX := count;
end;
begin
i:=2;
inc(powers[i], DivX);
i:=3;
while (i do
begin
inc(powers[i], DivX);
inc(i, 2);
end;
if x 1 then inc(powers[x]);
end;
var
i, total: longint;
begin
assign(a, 'input.txt');
reset (a);
readln(a, h);
for i := 1 to h do begin
read(a, next_number);
arr[i] := next_number;
end;
close(a);
for i := 1 to h do
Factorization(arr[i]);
total:=1;
for i := 1 to 10000 do begin
if powers[i] 0 then
total := total * succ(powers[i]);
end;
assign (b,'output.txt');
rewrite (b);
if (total = 10) and ((total mod 100) then write(b,'0');
writeln(b,(total mod 100));
close (b);
end.
Для вычисления простых чисел можно воспользоваться другими алгоритмами – решето Эратосфена:
program resheto;
const
n=10000;
type
mass=array[1..n]of integer;
var
s : mass;
i,k,m : integer;
begin
write('M= ');
readln(m);
for i:=2 to m do
s[i]:=1;
for i:=2 to m do
begin
if s[i]=1 then
begin
k:=i+i;
while kdo
begin
s[k]:=0;
k:=k+i;
end;
end;
end;
for i:=2 to m do
if s[i]=1
then write(i:5);
readln;
end.
Таким образом, попытка запрограммировать правило нахождения НОД из курса математики приводит к программному коду свыше 60-ти строк и очень трудному в объяснении и в понимании, так как не существует формулы для вычисления НОД(М, N) по значениям М и N.
Несмотря на то, что алгоритм Евклида был открыт около 2300 лет назад, он до сих пор остается отличным методом нахождения НОД.
Для "ручного" счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) заменить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
|
|
Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.
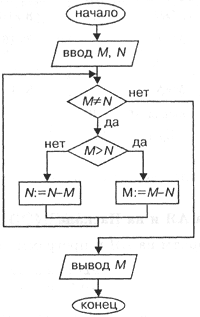
Описание алгоритма Евклида блок-схемой
На рис. приведена блок-схема алгоритма Евклида.
|
|
| Рис. Блок-схема алгоритма Евклида |
Структура алгоритма - цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
Программа на Паскале
Запишем программу на Паскале.
Program Evklid;
var M, N: longint;
begin
writeln('Введите М и N'); readln(M, N);
while MN do
if MN
then M:=M-N else N:=N-M;
write('Н0Д=',М)
end.
Очевидно, что алгоритм Евклида на языке Паскаль выглядит гораздо элегантнее и проще, чем попытка запрограммировать правило из курса математики. (для сравнения – всего 5строк кода на Паскале).
21
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт