Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf. Создание графических приложений: работа с графическим окном, динамические интерфейсные элементы
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf.»
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
2200 руб.
3140 руб.
1900 руб.
2710 руб.
1770 руб.
2530 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



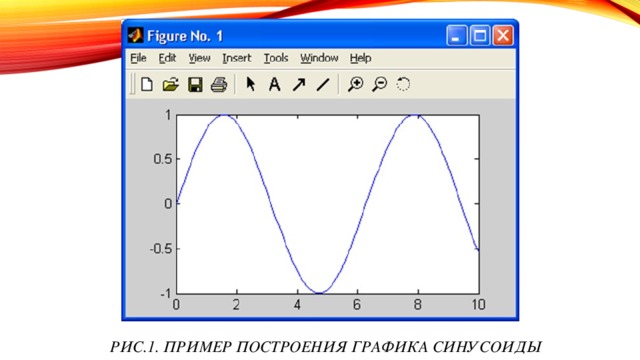
![Графики в полярной системе координат Построить графики функций y=sin(x) и y1=cos(x) . Модифицировать масштаб координатных осей графика. Сформируем массив Х приняв, что х изменяется в диапазоне [-8:8] с шагом 0,1, затем совместно сформируем массивы значений заданных функций с помощью следующей записи y=[sin(x); cos(x)]. С помощью функции plot2d построим графики функций y=sin(x) и y1=cos(x), установив значение параметра nax=[4,9,3,6]. Таким образом, ось X будет разбита 9 основными делениями (засечками), каждое основное 4 промежуточными, а ось Y соответственно - 6 и 3 (см. рис.).](https://fsd.kopilkaurokov.ru/up/html/2017/02/28/k_58b49593d33e4/img_user_file_58b495944938e_4.jpg)
 0 - поверхность имеет цвет «mode», выводится прямоугольная сетка. 0 - выводится прямоугольная сетка, заливка отсутствует (белый цвет). По умолчанию, равен 2 - цвет заливки синий, прямоугольная сетка выводится. type - позволяет управлять масштабом графика, по умолчанию имеет значение 2." width="640"
0 - поверхность имеет цвет «mode», выводится прямоугольная сетка. 0 - выводится прямоугольная сетка, заливка отсутствует (белый цвет). По умолчанию, равен 2 - цвет заливки синий, прямоугольная сетка выводится. type - позволяет управлять масштабом графика, по умолчанию имеет значение 2." width="640"
![Значения параметра type 0 - применяется способ масштабирования, как у ранее созданной графики. 1 - границы графика указываются вручную с помощью параметра ebox. 2 - границы графика определяют исходные данные. Box - определяет наличие рамки вокруг отображаемого графика. По умолчанию равен 4. Значения параметра box 0 и 1 - нет рамки 2 - только оси, находящиеся за поверхностью 3 - выводится рамка и подписи осей 4 - выводится рамка, оси и их подписи. ebox - определяет границы области, в которую будет выводиться поверхность, как вектор [xmin,xmax,ymin,ymax,zmin,zmax]. Этот параметр может использоваться только при значении параметра type=1. keyn=valuen - последовательность значений свойств графикаkey1=value1,key2=value2,...,keyn=valuen, таких как толщина линии, ее цвет, цвет заливки фона графического окна, наличие маркера и др. Таким образом, функцииplot3d (plot3d1) в качестве параметров необходимо передать прямоугольную сетку и матрицу значений в узлах сетки.](https://fsd.kopilkaurokov.ru/up/html/2017/02/28/k_58b49593d33e4/img_user_file_58b495944938e_7.jpg)

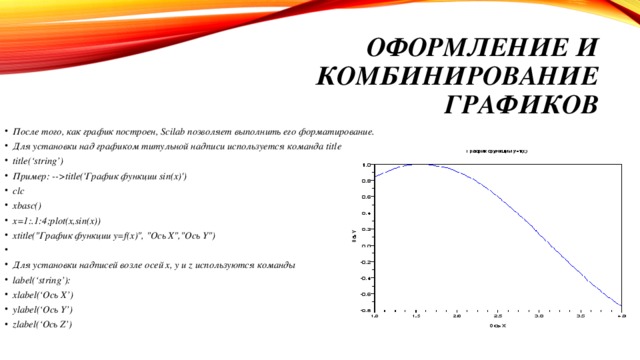
 legend(['sin(x)';'cos(x)';'sin(x)'],a=3); Для расположения нескольких графиков в одном окне без наложения их друг на друга используется команда subplot. Она должна стоять до оператора построения графика. subplot(m,n,p) или subplot(mnp) : m окон по горизонтали, n – по вертикали, p – номер окна, в которое будет выводиться текущий график (нумерация ведется по строкам). clf reset удаляет все подокна и возвращают графическое окно в обычное положение." width="640"
legend(['sin(x)';'cos(x)';'sin(x)'],a=3); Для расположения нескольких графиков в одном окне без наложения их друг на друга используется команда subplot. Она должна стоять до оператора построения графика. subplot(m,n,p) или subplot(mnp) : m окон по горизонтали, n – по вертикали, p – номер окна, в которое будет выводиться текущий график (нумерация ведется по строкам). clf reset удаляет все подокна и возвращают графическое окно в обычное положение." width="640"