11 класс. Тема "Моделирование".Метод Монте-Карло.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
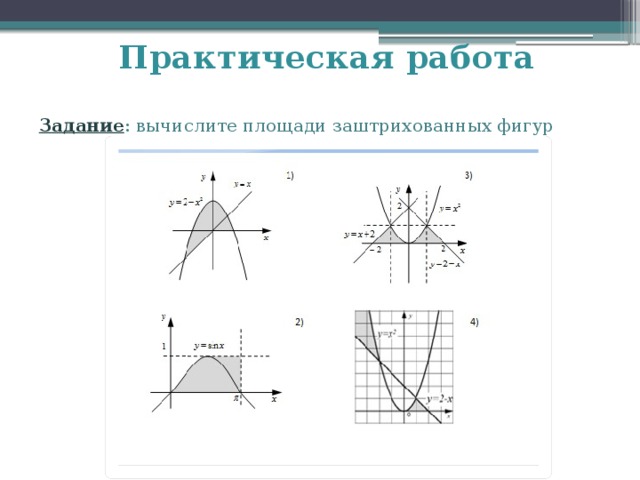
Различные способы вычисления площадей фигур.Метод Монте - Карло.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Различные способы вычисления площадей фигур.Метод Монте - Карло.»
Полезное для учителя
Распродажа видеоуроков!
2200 руб.
3140 руб.
1690 руб.
2420 руб.
2010 руб.
2870 руб.
1900 руб.
2720 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



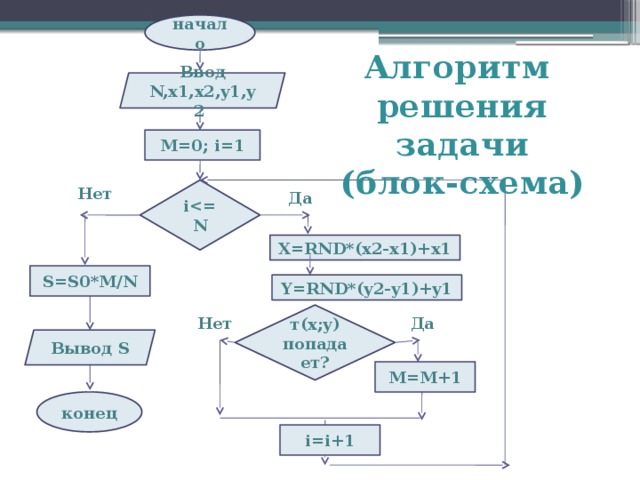
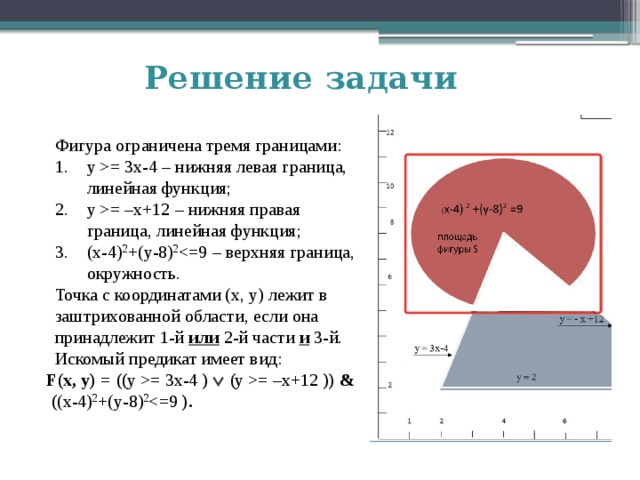 = 3x-4 – нижняя левая граница, линейная функция; y = –x+12 – нижняя правая граница, линейная функция; (x-4) 2 +(y-8) 2 Точка с координатами (x, y) лежит в заштрихованной области, если она принадлежит 1-й или 2-й части и 3-й. Искомый предикат имеет вид: F(x, y) = (( y = 3x-4 ) ( y = –x+12 )) & ( (x-4) 2 +(y-8) 2 )." width="640"
= 3x-4 – нижняя левая граница, линейная функция; y = –x+12 – нижняя правая граница, линейная функция; (x-4) 2 +(y-8) 2 Точка с координатами (x, y) лежит в заштрихованной области, если она принадлежит 1-й или 2-й части и 3-й. Искомый предикат имеет вид: F(x, y) = (( y = 3x-4 ) ( y = –x+12 )) & ( (x-4) 2 +(y-8) 2 )." width="640"
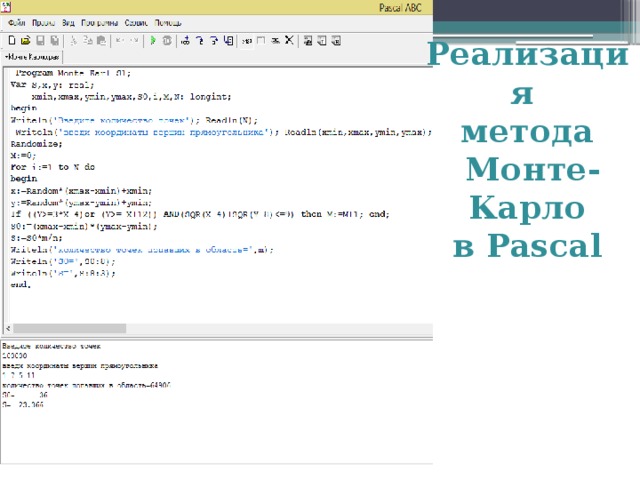
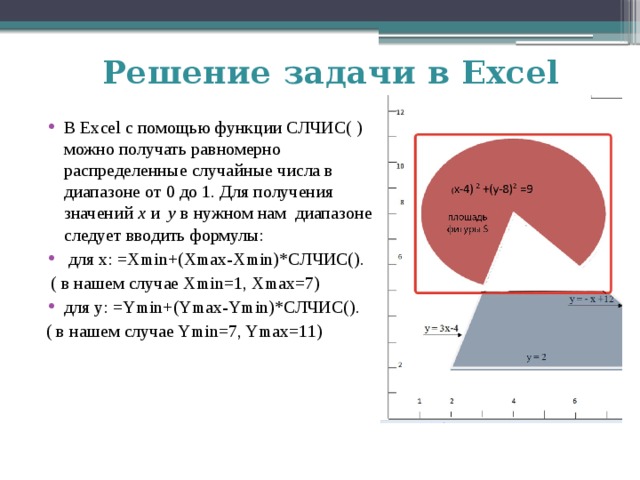
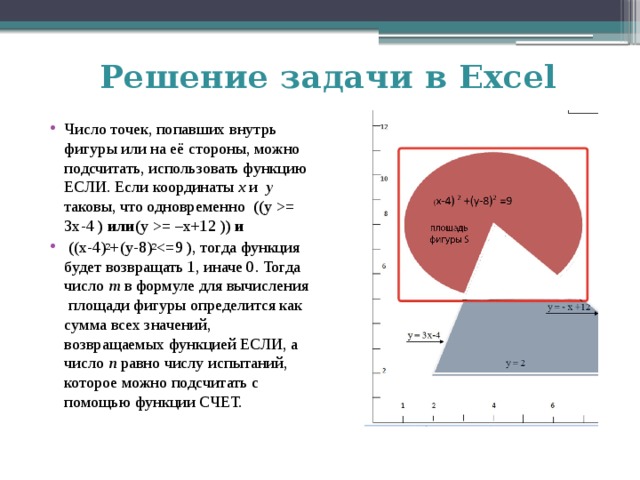
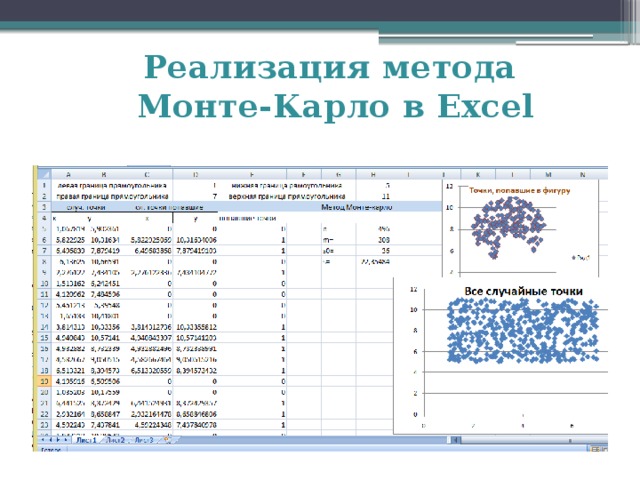
 =-a3+12)));1;0) =1+6*СЛЧИС() … … =7+4*СЛЧИС() =если(и(((a102-4)^2+(b102-8)^2=3*a102-4);(b102=-a102+12)));1;0)" width="640"
=-a3+12)));1;0) =1+6*СЛЧИС() … … =7+4*СЛЧИС() =если(и(((a102-4)^2+(b102-8)^2=3*a102-4);(b102=-a102+12)));1;0)" width="640"