Презентация к уроку информатики: "Вычисление определителей".

Вычисление численных определителей.

Информатика

(профиль – реальный)

Матрицы

• — это прямоугольные таблицы из чисел, содержащие m строк и n столбцов.
• Числа m и n называются порядками матрицы.

Ма́трица

• — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы допускают следующие алгебраические операции :

• сложение матриц , имеющих один и тот же размер;
• умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);
• умножение матрицы на элемент основного кольца или поля (т. н. скаляр).

Матрицы записываются с помощью больших круглых скобок

a11 a12 … a1n

a21 a22 … a2n

. . . . . . . . . . . . . . .

am1 am2 … amn

Диагонали матриц

Сложение матриц

Для обозначения произведения матрицы на число используется запись: С=А*λ= λ*А

Перемножение (произведение) матриц

Условие перемножения (произведения) матриц

• Матрицу A можно умножить не на всякую матрицу B . Необходимо, чтобы число столбцов матрицы A было равно числу строк матрицы B
• Оба произведения A·B и B·A можно определить только в том случае, когда число столбцов A совпадает с числом строк B, а число строк A совпадает с числом столбцов B. При этом обе матрицы A·B и B·A будут квадратными, но порядки их будут разными.
• Чтобы оба произведения A·B и B·A были определены и имели одинаковый порядок, необходимо и достаточно, чтобы матрицы A и B были квадратными матрицами одного порядка.

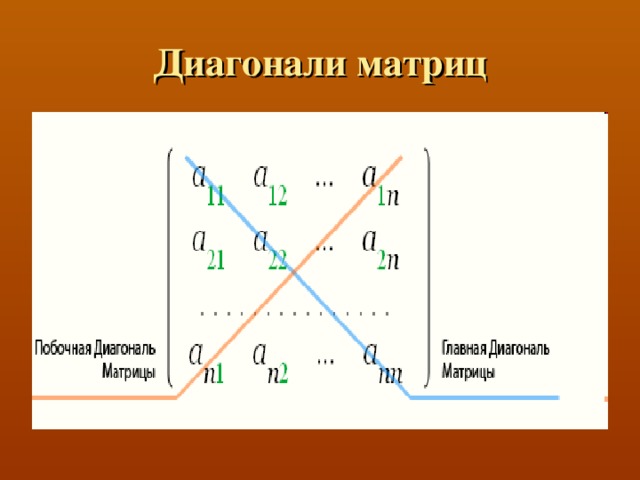
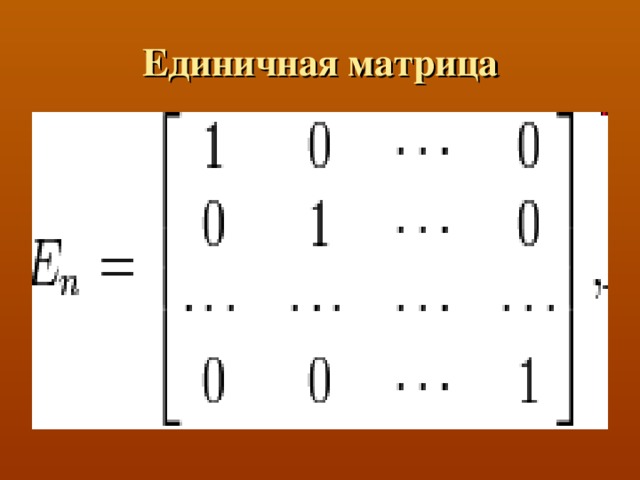
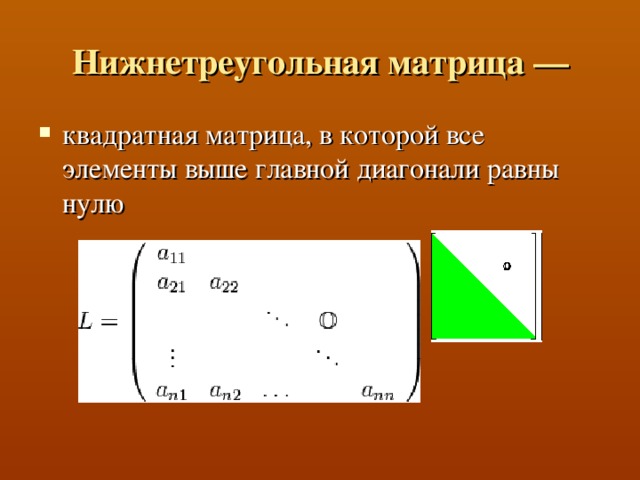
• В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Единичная матрица

Единичные матрицы первых порядков имеют вид

Симметричная матрица

• Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали.

Кососимметричная (кососимметрическая)

• матрица — квадратная матрица А над полем k характеристики, отличной от 2, удовлетворяющая соотношению:

A T = − A,

где A T — транспонированная матрица.

Кососимметричная матрица

0 а

-а 0

Верхнетреугольная матрица —

• квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица —

• квадратная матрица, в которой все элементы выше главной диагонали равны нулю

Определи́тель (или детермина́нт) —

одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Алгоритм вычисления определителя матрицы:

Для матрицы первого порядка детерминантом является сам

единственный элемент этой матрицы:

Для матрицы 2х2 детерминант определяется как

Для матрицы n порядка определитель задаётся рекурсивно:

где М 1 j — дополнительный минор к элементу a 1j .

Эта формула называется разложением по строке.

Для вычисления определителей

можно применить два алгоритма: рекурсивный

и

итеративный

.

Возьмём произвольный минор М 1 j.

Он является определителем матрицы порядка n-1. Для его нахождения необходимо решить такую же задачу, только меньшей размерности.

Следовательно, необходимо применить рекурсивный алгоритм.

Число операций,

Необходимых для рекурсивного вычисления определителя матрицы порядка n, определяется количеством рекурсивных вызовов, а также числом операций, совершаемых во время одного вызова.

Недостаток рекурсивного алгоритма:

Количество операций при каждом вызове пропорционально n 2 . Следовательно, временная сложность алгоритма равна Q(n 2 n!), что делает малоэффективным для больших значений n.

Итеративный алгоритм:

использует элементарные преобразования, приводящие матрицу к треугольному виду. Определитель такой матрицы равен произведению значений элементов, находящихся на главной диагонали.

Недостаток итеративного метода:

Производится большое количество операций деления. Большие колебания значений элементов матрицы приводят к значительным погрешностям.

Реализация на Паскале рекурсивной функции вычисления определителей:

Function cdet(var x:mat; t:integer):real;

var i, j, k : integer;

s : real;

minor : mat;

Begin

if t=1 then calcul:=x[1,1] {элементарный случай}

else begin

s:=0;

for k:=1 to t do begin

for i:=1 to t+1 do

for j:=1 to k-1 do minor[I,j]:=x[i+1,j];

for i:=1 to t+1 do

for j:=k to t+1 do minor [I,j]:=x[i+1, j+1];

if odd(k) then s:=s+x[1,k]*cdet(minor, t-1) {рекурсивный вызов}

else s:=s-x[1,k]*cdet(minor, t-1);

end;

cdet:=s;

end;

end.;

Реализация на Паскале итеративной функции вычисления определителей:

Function CID(x:mat; r:integer): real;

var i, j, k : integer;

q : real;

Begin {CID}

for i:=1 to r-1 do begin

if x[I,i]:=0 then

begin

k:=1;

for j:=i+1 to r do

if x[j,i]0 then k:=j;

if k=1 then begin CID:=0 ; exit; end

else

for j:=1 to r do

begin

q:=x[i,j];

x[i,j]:=x[k,j];

x[k,j]:=-q;

end;

end;

Реализация на Паскале итеративной функции вычисления определителей:

{ преобразование строк с целью обнуления элементов в столбце i, расположенных под диагональю }

for j:=i+1 to x do

begin

q:=-x[j,i]/x[I,i];

for k:=1 to r do x[j,k]:=x[j,k]+x[I,k]*q;

end;

end;

{ вычисление значения определителя треугольной матрицы }

q:=1;

for i:=1 to r do q:=q*x[I,i];

CID:=q ;

End;

Домашнее задание: