Презентация к уроку информатики: "Метод greedy".

11 класс

Тема урока:

Метод Greedy

– “ жадный алгоритм”

Описание метода

Данным методом решаются задачи, имеющие следующую структуру:

• задано множество А = { а 1 , а 2 ,…, а п }, образованное из n элементов;
• необходимо определить подмножество В, где В- это подмножество А, удовлетворяющее определённым условиям, которое в результате и будет решением задачи .

Общая схема алгоритма метода Greedy

Функция ExistaElemente возвращает значение true, если в множестве А существуют элементы, удовлетворяющие условию отбора.

Метод Greedy может быть реализован с помощью цикла:

while ExistaElemente do

begin

AlegeUnElement (x) ;

IncludeElementul (x) ;

end;

Процедура AlegeUnElement извлекает из множества А рассматриваемый элемент х

Процедура IncludeElementul записывает выбранный элемент в подмножество В. {подмножество В первоначально является пустым}

Сущность метода

Как видим, в методе Greedy решение задачи определяется путём последовательной проверки элементов множества А и включения некоторых из них в подмножество В. Тестируется первый элемент множества А, второй, третий…,пока не будут протестированы все – отсюда и название метода Greedy .

Greedy – жадный, ненасытный

0. напишите программу, которая вычисляет подмножество В, из множества А, такое, чтобы сумма элементов подмножества В была максимальна. Например, для А={ 21,5; -3,4; 0; -12,3; 83,6} получим В={ 21,5; 83,6 }" width="640"

Задача:

Рассмотрим множество А= {а 1 , а 2 ,…, а п }, элементы которого являются веществен-ными числами и хотя бы один из них удовлетворяет условию а i 0. напишите программу, которая вычисляет подмножество В, из множества А, такое, чтобы сумма элементов подмножества В была максимальна.

Например, для А={ 21,5; -3,4; 0; -12,3; 83,6} получим В={ 21,5; 83,6 }

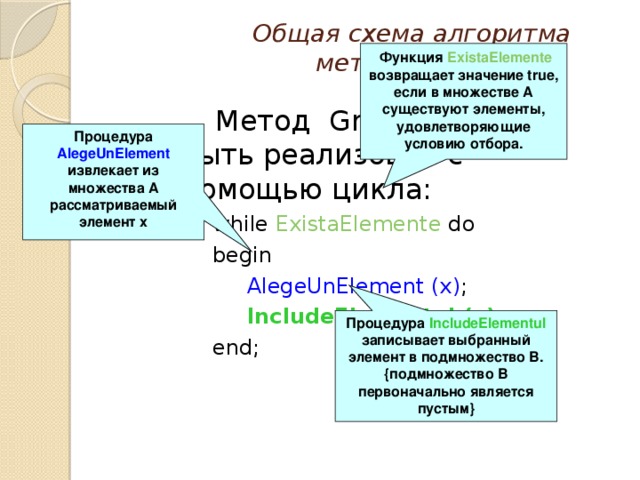
Решение задачи

Чтобы избежать полного перебора всевозможных подмножеств А i , А i , А, в методе Greedy применяется критерий прямого выбора необходимых элементов из множества А.

В данной задаче условие отбора очень простое: на каждом шаге в подмножество В включается любой положительный элемент множества А.

Program Greedy ;

const nmax = 1000 ;

var A , B: array [ 1..nmax ] of real ;

i, n : 1..nmax ;

m : 0..nmax ;

x : real ;

Представляем множества А и В в виде одномерных массивов

Количество элементов множества В

0 then ExistaElemente := true ; end ; { ExistaElemente } procedure AlegeUnElement ( var x : real ) ; var i : integer ; begin i := 1 ; while A [ i ] x := A [ i ] ; A [ i ] := 0 ; End ; { AlegeUnElement } procedure IncludeElementul ( x: real ) ; begin m := m + 1; B [ m ] := x ; End ; { IncludeElementul }" width="640"

Обратите внимание, процедура AlegeUnElement обнуляет компоненту массива А, содержащую элемент х, извлечённый из соответствующего множества

Function ExistaElemente : boolean ;

var i : integer ;

begin

ExistaElemente := false ;

for i:=1 to n do

if A [ i ] 0 then ExistaElemente := true ;

end ; { ExistaElemente }

procedure AlegeUnElement ( var x : real ) ;

var i : integer ;

begin

i := 1 ;

while A [ i ]

x := A [ i ] ;

A [ i ] := 0 ;

End ; { AlegeUnElement }

procedure IncludeElementul ( x: real ) ;

begin

m := m + 1;

B [ m ] := x ;

End ; { IncludeElementul }

BEGIN

write ( ‘Введите n=’ ); readln ( n ) ;

writeln ( ‘Введите элементы множества А:’ );

for i: = 1 to n do

read ( A[ i ] );

writeln ;

m := 0;

while ExistaElemente do

begin

AlegeUnElement ( x ) ;

IncludeElementul ( x ) ;

end;

writeln ( ‘Элементы множества В :’ );

for i := 1 to n do

writeln ( B[ i ] );

readln;

end.

Выводы :

• Этот метод кажется простым, но прямой выбор не всегда легко осуществить, иногда требуется предварительная сортировка.
• Временная характеристика алгоритмов по методу Greedy значительно ниже, чем в алгоритмах, использующих при решении тех же задач метод полного перебора .

Удачи при решении задач!

Домашнее задание:

§ 5.2, конспект.