Практика информационного моделирования на графах
Методическое пособие
по составлению расписания
Учитель Ю. Хапий
МБОУ СОШ № 10 «Успех» г. о. Самара Самара, 2013
Проблема
Создание расписания
при свободном выборе предметов
каждым учащимся
с соблюдением правил:
не более одного испытания в день,
количество дней для проведения экзаменов - минимально
Цель
Разработка пошаговой технологии составления расписания
с учетом выбранных предметов учащимся
при условиях:
не более одного испытания в день,
наименьшего числа экзаменационных дней
Задачи
Изучить примеры
информационного моделирования на графах
в сфере практической деятельности людей.
Применить
информационное моделирование на графах
при разработке пошаговой технологии
составления расписания
Основные понятия теории
Граф – это средство
для наглядного представления
состава и структуры системы,
состоящий из вершин
(могут изображаться плоскими фигурами),
связанных (соединенных) дугами
(направленные линии со стрелкой)
или ребрами
(ненаправленные линии без стрелки,
заменяющие противоположно направленные дуги).
Основные понятия теории
Две вершины, соединенные дугой или ребром, называются смежными.
При представлении состава и структуры системы
в виде графа компоненты системы изображаются вершинами, а связи между ними –
линиями (дугами или ребрами).
Взвешенный (размеченный) граф – это граф,
в котором с вершинами или линиями
связана дополнительная информация,
называемая весом вершины или линии.
Типичные примеры
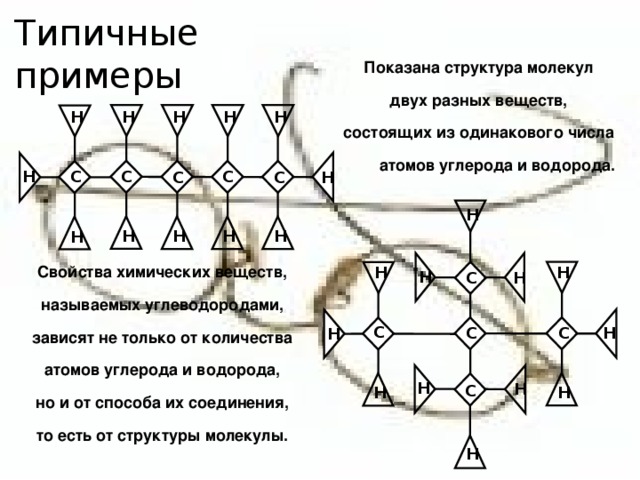
Показана структура молекул
двух разных веществ,
состоящих из одинакового числа атомов углерода и водорода.
Н
Н
Н
Н
Н
С
С
Н
С
С
С
Н
Н
Н
Н
Н
Н
Н
Свойства химических веществ,
называемых углеводородами,
зависят не только от количества
атомов углерода и водорода,
но и от способа их соединения,
то есть от структуры молекулы.
Н
Н
Н
Н
С
С
С
С
Н
Н
Н
Н
С
Н
Н
Н
Типичные примеры
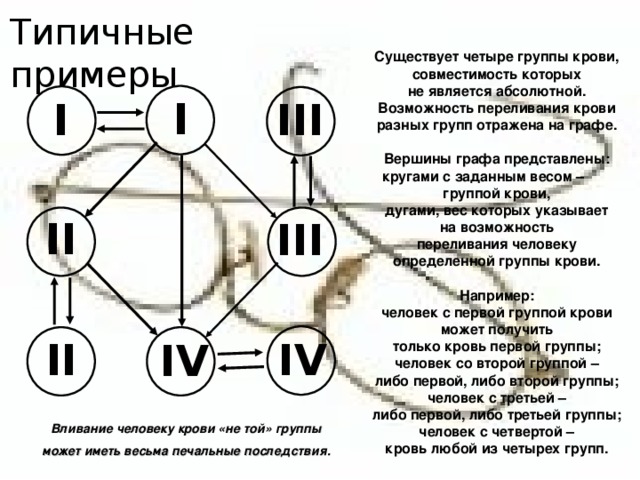
Существует четыре группы крови,
совместимость которых
не является абсолютной.
Возможность переливания крови разных групп отражена на графе.
Вершины графа представлены:
кругами с заданным весом – группой крови,
дугами, вес которых указывает
на возможность
переливания человеку
определенной группы крови.
Например:
человек с первой группой крови
может получить
только кровь первой группы;
человек со второй группой –
либо первой, либо второй группы;
человек с третьей –
либо первой, либо третьей группы;
человек с четвертой –
кровь любой из четырех групп.
I
I
III
II
III
II
IV
IV
Вливание человеку крови «не той» группы
может иметь весьма печальные последствия.
Постановка задачи
Известен список учащихся и перечень предметов,
а также выбор предметов из перечня,
сделанный каждым экзаменующимся.
Требуется составить расписание
прохождения испытаний
каждым учащимся по выбранным предметам.
Расписание считается составленным,
если в нем соблюдаются принципы:
сдача одним школьником в один день
только одного предмета;
число экзаменационных дней – минимально.
Математическая запись задачи
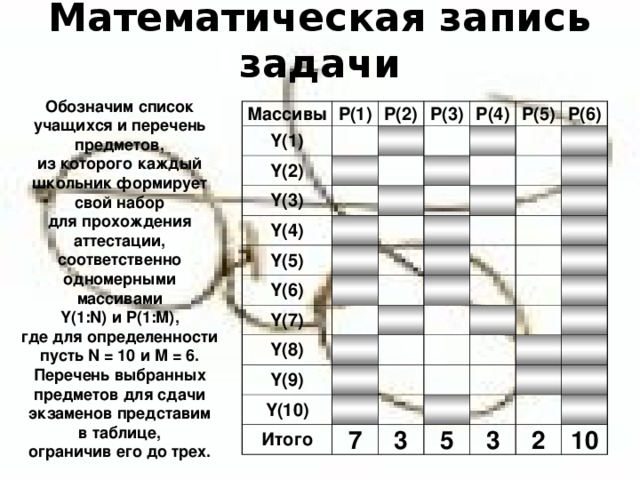
Обозначим список учащихся и перечень предметов,
из которого каждый школьник формирует свой набор
для прохождения аттестации, соответственно одномерными массивами
Y( 1 :N) и P( 1 :M) ,
где для определенности пусть N = 10 и M = 6 .
Перечень выбранных предметов для сдачи экзаменов представим
в таблице,
ограничив его до трех.
Массивы
P(1)
Y(1)
P(2)
Y(2)
P(3)
Y(3)
Y(4)
P(4)
P(5)
Y(5)
P(6)
Y(6)
Y(7)
Y(8)
Y(9)
Y(10)
Итого
7
3
5
3
2
10
Изображение задачи в виде графа
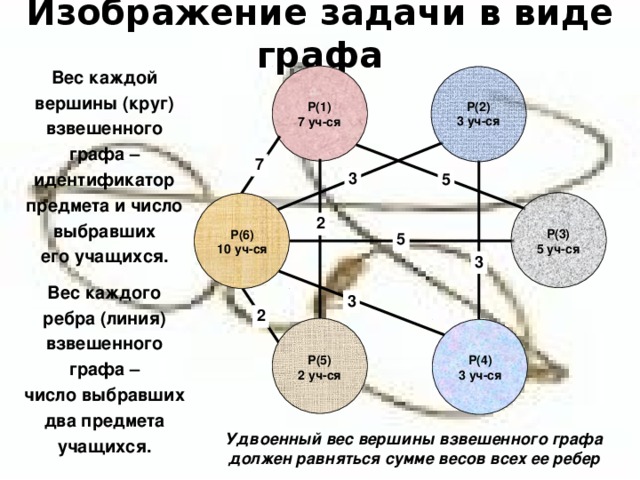
Вес каждой
вершины (круг)
взвешенного
графа –
идентификатор
предмета и число
выбравших
его учащихся.
Вес каждого
ребра (линия)
взвешенного
графа –
число выбравших два предмета
учащихся.
Р(2)
3 уч-ся
Р(1)
7 уч-ся
7
3
5
2
Р(3)
5 уч-ся
Р(6)
10 уч-ся
5
3
3
2
Р(5)
2 уч-ся
Р(4)
3 уч-ся
Удвоенный вес вершины взвешенного графа
должен равняться сумме весов всех ее ребер
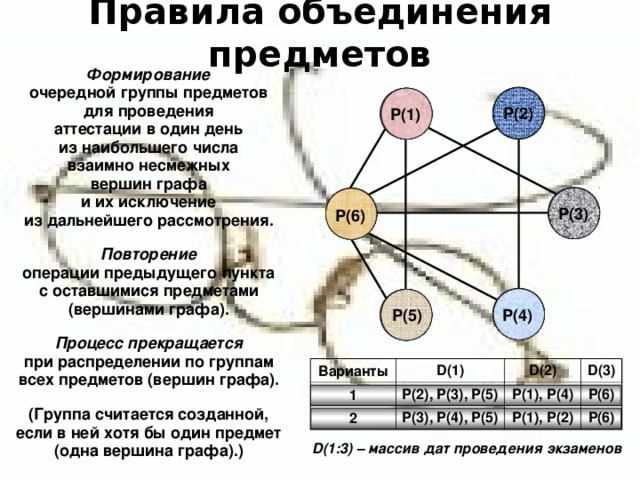
Правила объединения предметов
Формирование
очередной группы предметов
для проведения
аттестации в один день
из наибольшего числа
взаимно несмежных
вершин графа
и их исключение
из дальнейшего рассмотрения.
Повторение
операции предыдущего пункта
с оставшимися предметами
(вершинами графа).
Процесс прекращается
при распределении по группам
всех предметов (вершин графа).
(Группа считается созданной,
если в ней хотя бы один предмет
(одна вершина графа).)
Р(2)
Р(2)
Р(2)
Р(1)
Р(1)
Р(1)
Р(3)
Р(3)
Р(3)
Р(6)
Р(6)
Р(6)
Р(5)
Р(5)
Р(5)
Р(4)
Р(4)
Р(4)
Варианты
1
D(1)
D(2)
2
P(2) , P(3) , P(5)
D(3)
P(3) , P(4) , P(5)
P(1) , P(4)
P(1) , P(2)
P(6)
P(6)
D(1:3) – массив дат проведения экзаменов
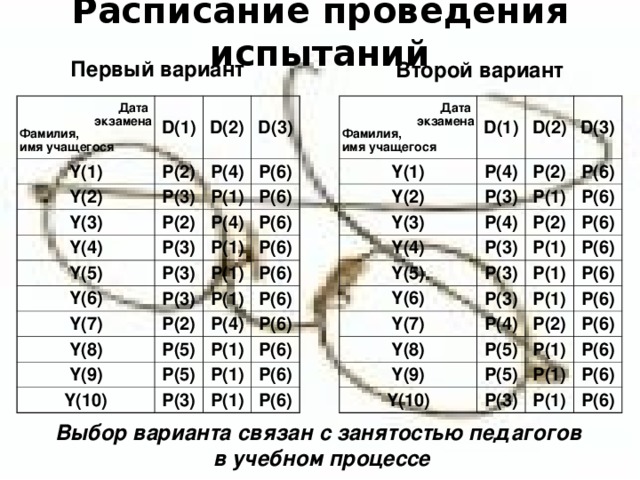
Расписание проведения испытаний
Первый вариант
Второй вариант
Дата
экзамена
Фамилия,
имя учащегося
Дата
экзамена
Фамилия,
имя учащегося
D(1)
Y(1)
Y(1)
D(1)
D(2)
Р(2)
Y(2)
Y(2)
Р(4)
D(2)
D(3)
Y(3)
Р(3)
Р(2)
D(3)
Y(3)
Р(3)
Р(4)
Р(1)
Р(4)
Y(4)
Р(1)
Р(6)
Р(6)
Р(2)
Y(4)
Y(5)
Р(6)
Р(3)
Р(3)
Р(4)
Р(2)
Y(5)
Р(6)
Р(1)
Р(6)
Р(1)
Р(3)
Р(3)
Р(6)
Y(6)
Y(6)
Р(6)
Р(1)
Р(6)
Р(1)
Y(7)
Y(7)
Р(3)
Р(3)
Р(6)
Р(6)
Р(1)
Р(1)
Y(8)
Y(8)
Р(4)
Р(2)
Y(9)
Р(5)
Р(2)
Р(6)
Р(6)
Y(9)
Р(4)
Р(5)
Y(10)
Р(5)
Y(10)
Р(6)
Р(6)
Р(1)
Р(1)
Р(5)
Р(3)
Р(1)
Р(6)
Р(6)
Р(3)
Р(1)
Р(6)
Р(6)
Р(1)
Р(1)
Р(6)
Р(6)
Выбор варианта связан с занятостью педагогов
в учебном процессе
Выводы
Представленный метод составления расписания
успешно используется
в МБОУ СОШ № 10 «Успех» г. о. Самара.
В случае написания компьютерной программы
по описанному алгоритму
процесс «ручного» составления расписания
можно заменить на автоматизированный