Основы логики(практика)

ОСНОВЫ ЛОГИКИ Разработка: Ерошенко И.В. – учитель информатики и ИКТ Муниципального бюджетного общеобразовательного учреждения "Великомихайловская средняя общеобразовательная школа Новооскольского района Белгородской области, 2014-2015 уч. год. в презентации доходчиво произведен разбор задач ЕГЭ по информатике А3,А10,В15

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Основы логики(практика) »

ПРАКТИКА

Учитель информатики МБОУ «Великомихайловская СОШ Новооскольского района Белгородской области» Ерошенко И.В.

Найди верное определение

Форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение

Форма мышления, фиксирующая существенные признаки объекта

Наука о формах и способах мышления

Высказывание, построенное на основании простых высказываний

Логика

Умозаключение

Понятие

Высказывание, не соответствующее действительности

Ложь

Составное

Решение задач

Даны высказывания s=Число 3 является делителем числа 198, x=Иркутск – столица Франции. Сформулировать на обычном языке высказывания: A = ¬S; B = x & s; C=s  x; D = s  ¬ x; M = x  s. Определить их истинность.
Пусть n=1, m=0. Определить истинность высказывания

Построить таблицу истинности выражений:

4. Пусть A=0, B=1. Определить истинность высказывания F = (A  B) & ( ¬ A  ¬ B).

5. Построить таблицу истинности следующих выражений:

6. ЗАДАЧИ ЕГЭ ПО ИНФОРМАТИКЕ

А3

В15

А10

Проверка задач

Число 3 не является делителем числа 198. (ложь)

Иркутск – столица Франции, а число 3 является делителем числа 198. (ложь).
Число 3 является делителем числа 198, или Иркутск – столица Франции. (истина).
Если число 3 является делителем числа 198, то Иркутск – не столица Франции. (истина).
Иркутск – столица Франции тогда и только тогда, когда число 3 является делителем числа 198. (ложь)

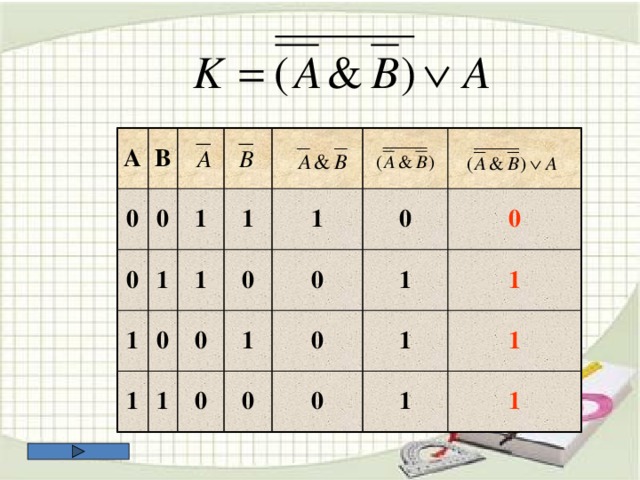
A B 0 0 0 1 1 1 1 1 1 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1

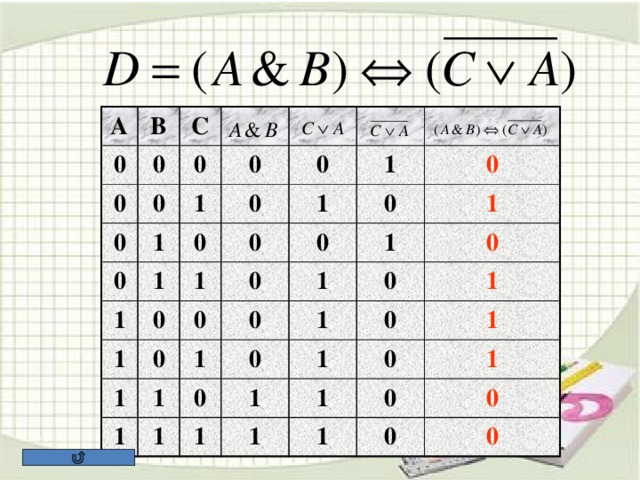
A B 0 C 0 0 0 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 0 0 1 1 0 1 1 1 1 1 0 0 1 0 0 1 0 1 1 1 0 1 1 1 0 1 1 0 0 0

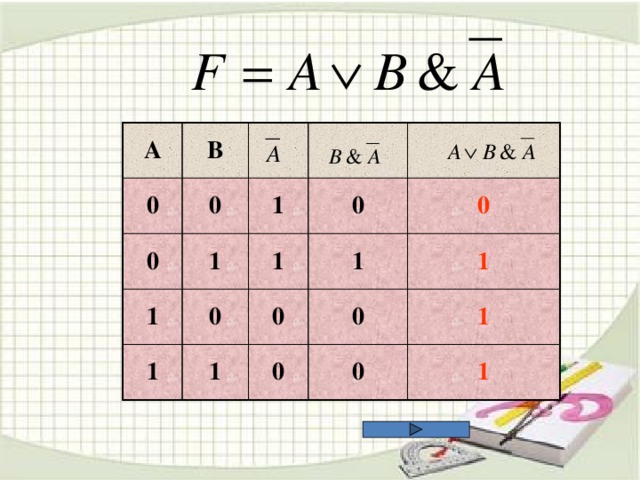
A B 0 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 0 0 1 1

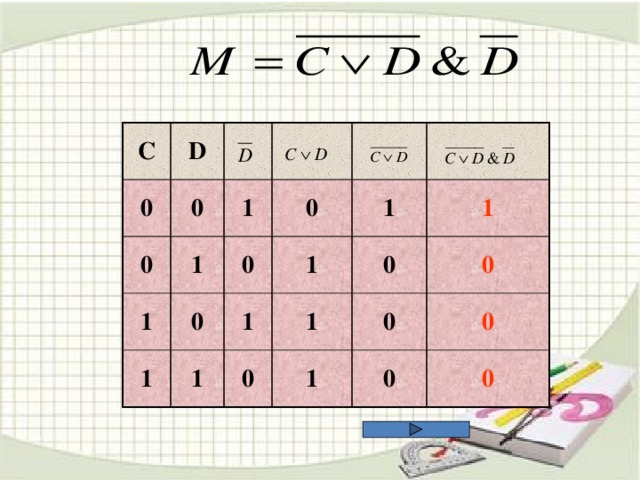
C D 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 0 0 0

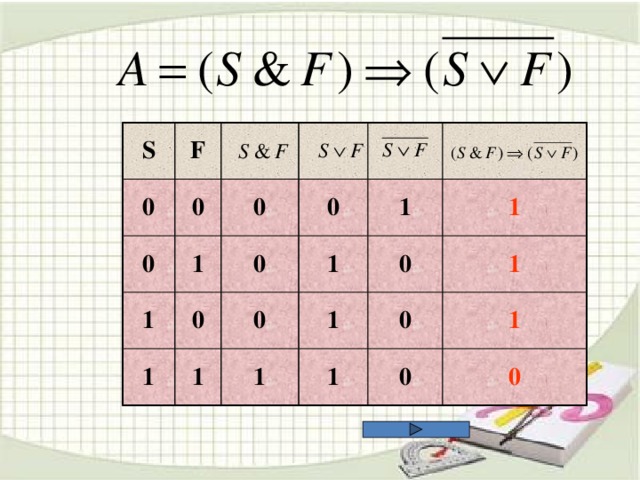
S F 0 0 0 0 1 1 0 0 0 1 1 1 1 0 1 1 0 1 0 1 1 1 0 0

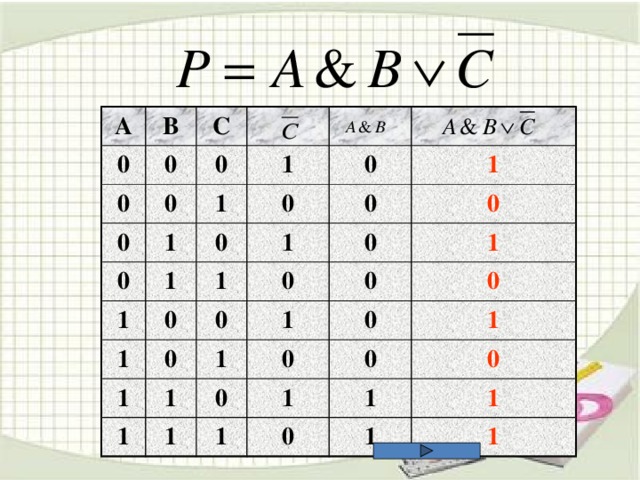
A 0 B 0 C 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 0 0 1 1 0 1 1 0 0 1 1 1

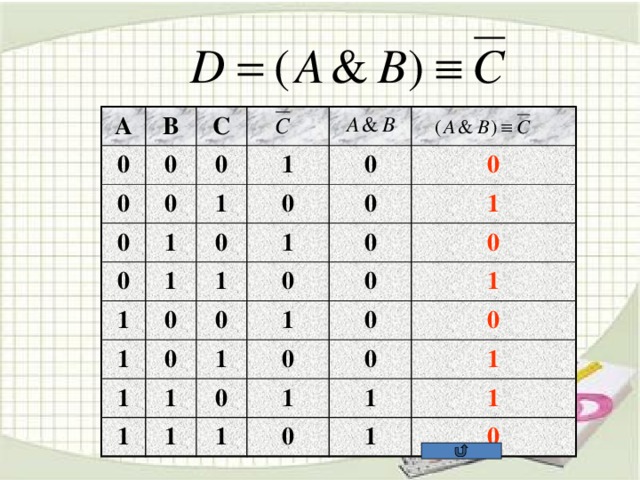
A B 0 0 0 C 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 0 1 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 0 0 1 1 1 1 0

ЗАДАЧА А3

Дан фрагмент таблицы истинности выражения F:

Какое выражение соответствует F?

1) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 4) ¬x1 ∧ x2 ∧ x3 ∧ x4 ∧ ¬x5

Пояснение .

Посмотрим внимательно на ответы. Они представляют собой либо конъюнкцию, либо дизъюнкцию данных пяти переменных или отрицательных к ним.

Сначала выясним, конъюнкция это или дизъюнкция.

Дизъюнкция не может принимать значение ноля дважды из трех разных комбинаций, следовательно, в ответе должна быть конъюнкция. Вычеркиваем 1 и 2 варианты ответа.

Из 3 и 4 вариантов подходит 4. Правильный ответ - 4.

ЗАДАЧА В15

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1

x1 ∨ y1 = 1

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Пояснение .

1) Из последнего уравнения следует, что глобально мы имеем три варианта - x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.

2) Логическое И истинно, только тогда, когда истины все утверждения, а импликация ложна только в случае, если из истинного следует ложное.

3) Уравнение (1) описывает ряд переменных {x1, x2, x3, x4, x5}. Так как из переменной с более низким номером всегда следует переменная с более высоким, если любую переменную из этого ряда приравнять 1, то все следующие должны также быть равны 1. Для уравнения (2) существует то же самое правило. Иначе говоря, если записать переменные x (или y) в порядке возрастания их номеров, слева будут нули, а справа - единицы.

4) Рассмотрим вариант x1=1, y1=1. Так как первые числа каждого ряда равны 1, то все следующие тоже равны 1. Существует только одна комбинация для этого варианта.

5) Рассмотрим вариант x1=0, y1=1. Для y-ряда все переменные равны 1, для x же существует 5 комбинаций, так как в ряде x может быть от 1 до 5 нолей включительно.

6) Последний вариант рассмотрим аналогично предыдущему. Там существует всего 5 комбинаций.

Правильный ответ: 5+5+1=11 комбинаций .

ЗАДАЧА А10

На числовой прямой даны два отрезка: P =[5,15] и Q =[11,21]. Выберите такой отрезок A , что формула (( x ∈А)→¬( x ∈ Q ))∨( x ∈ P ) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1.[4;34]

2. [4;24]

3. [4;14]

4. [14;24]

Пояснение .

Преобразуем выражение – заменим импликацию дизъюнкцией. Получим: (¬( x ∈А))∨(¬( x ∈ Q ))∨( x ∈ P ) Выражение (¬( x ∈ Q ))∨( x ∈ P ) истинно для тех только тех x , которые либо лежат в P , либо не лежат в Q , иными словами – для x ∈ R , где R =(−∞,15]∪(21,+∞). Выражение (¬( x ∈ A ))∨( x ∈ R ) тождественно истинно тогда и только тогда, когда A ⊆ R . Этому условию удовлетворяет только отрезок [4,14].