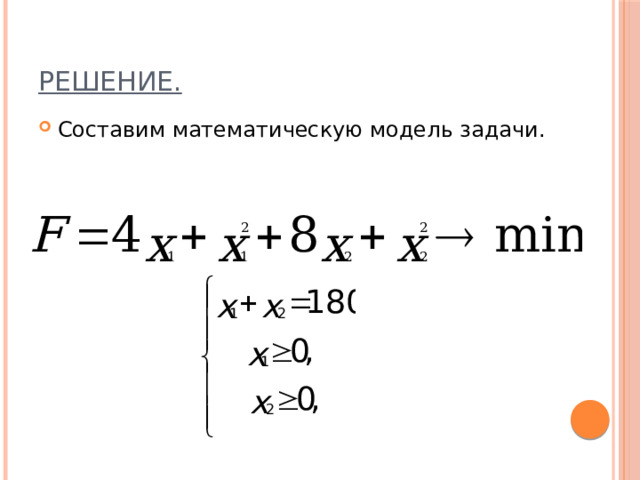в данной работе рассматривается метод множителй Лагранжа в задачах нелинейного программирования
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Метод множителей Лагранжа в задачах нелинейного программирования
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Метод множителей Лагранжа в задачах нелинейного программирования»
Полезное для учителя
Распродажа видеоуроков!
1770 руб.
2530 руб.
1690 руб.
2420 руб.
1330 руб.
1900 руб.
1860 руб.
2660 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства