| 1.Организационный момент, 2 минуты |
— Доброе утро! Сегодня у нас очень важный урок. Вам предстоит совершить «открытие», которому посвящена тема урока.
— Урок будет проходить в форме диалога, беседы, обсуждения решения определённых заданий. (Слайд 2) — Девизом сегодняшнего урока будут слова Дьёрдя Пойа «Лучший способ изучить что-либо – это открыть самому». — Давайте последуем совету венгерского математика. Надеюсь на вашу активность на уроке.
— Для улучшения внимания, ясности восприятия и речи проведём небольшую разминку, сделав упражнение «Шапка для размышлений». «Наденьте шапку», т.е. мягко заверните уши от верхней точки до мочки три раза.
|
Слушают вступительную речь учителя.
Выполняют упражнение для улучшения внимания, ясности восприятия и речи. |
К уроку учащиеся приготовили учебник, тетрадь «Открытий», тетрадь с домашней работой, инструменты, дневник. |
| 2. Актуализация знаний, 5 минут
3. Формирование новых знаний, 18 минут
4. Первичное закрепление, 10 минут
5. Задание на дом, 2 минуты.
6. Рефлексия, 3 минуты | — Для успешной и более продуктивной работы на уроке нам необходимо повторить признаки параллельности прямых и признаки подобия треугольников. (Слайд 3)
— Используя рисунки на слайде сформулируйте признаки параллельности прямых.
— Молодцы! — Работаем дальше. Вспомним признаки подобия треугольников. (Слайд 4) — Закончите фразу: «Для того чтобы доказать подобие треугольников по первому признаку подобия необходимо доказать, что… —Верно. — Повторим суть третьего признака подобия треугольников. Обратите внимание на экран. (Слайд 5) — Выберите рисунок, на котором треугольники подобны по третьему признаку? Свой ответ аргументируйте.
(Слайд 6)
—Теперь повторим второй признак подобия треугольников. У вас на столах карточки с заданием, которые вы будете выполнять в паре. То же самое задание вы можете увидеть на экране. (Слайд 7) Задание: Какие названия элементов треугольников должны стоять вместо каждого из пропусков в формулировке второго признака подобия треугольников? —Обсудите в паре выбранный вами ответ и впишите его в данную карточку.
—Проверяем. (спросить какого-нибудь ученика) Внимание на слайд с ответом. (Слайд 8)
—У кого получилось также как на экране?
—Молодцы!
— Мы с вами повторили все три признака подобия треугольников. А вы знаете ли вы, что треугольник — замечательная геометрическая фигура и самая популярная в школьной программе по геометрии. Многие известные мыслители прошлого обращались к темам о замечательных точках и линиях треугольника. —Назовите эти линии.
—Сколько медиан, биссектрис, высот можно провести в произвольном треугольнике? —А каким замечательным общим свойством они обладают? (Слайд 9)
— Оказывается это ещё не все линии, о которых можно вести речь, работая с треугольником. (Слайд 10) —Внимание на слайд. Рассмотрите рисунок и скажите, что общего у треугольников, изображённых на нём.
—Каждый отрезок в треугольнике что-то «делает». Например, медиана треугольника — это отрезок, который…… —Биссектриса угла треугольника — это отрезок, который выходит из вершины угла и ……. —А этот отрезок что делает?
— И название этого отрезка вам легко будет запомнить, по тому, что он делает - соединяет середины двух сторон треугольника и, поэтому называется средней линией треугольника. — Приготовьте тетрадь «Открытий» и запишите тему урока: «Средняя линия треугольника». Выполните чертёж и запишите определение средней линии треугольника. (Слайд 11)
— Рассмотрим задачу: (Слайд 12) Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника. —Сможем ли мы, опираясь только на определение средней линии треугольника и на имеющиеся у нас знания, решить задачу?
—Каких знаний у нас не хватает?
—Вы знаете, оказывается, есть такая теорема, которая поможет нам решить эту задачу. Сейчас мы вместе будем доказывать теорему о средней линии треугольника несколько непривычным для вас способом. Начнём сразу со слова «доказательство». У вас на столах лежат заготовки для доказательства теоремы о средней линии треугольника, в которых вы будете работать, а потом приклеите их в тетрадь «Открытий».
—Доказательство: Рассмотрим треугольник MBN и треугольник АВС. Что вы о них можете сказать?
— Запишем сделанный нами вывод как гипотезу теоремы о средней линии треугольника. Впишем полученный факт в то, что надо «доказать» в теореме под номером 1.
— Какой вывод можно сделать о длинах сторон MN и AC?
— Запишем как ещё одну гипотезу полученный факт в то, что надо «доказать» в теореме под номером 2
— А теперь попробуйте сформулировать теорему о средней линии треугольника.
— Давайте, на всякий случай, сверимся с материалом учебника. (Стр. 146)
— А теперь при помощи выведенной нами теоремы решим задачу. (Слайд 12) (Предложить какому–нибудь ученику поработать у доски; поставить ему отметку за решение)
— А сейчас перейдём к практическому применению выведенной нами теоремы при решении задач. Решим задачу № 565 из учебника. (Предложить какому-то ученику поработать у доски; поставить ему отметку за решение)
— А сейчас мы выполним самостоятельную работу, где сможем применить полученные на сегодняшнем уроке знания. Работу мы тут же оценим. Заданий в работе пять. За пять правильно выполненных заданий – отметка 5, за четыре – отметка 4 и т.д. Выполняйте мини-решение в тетради «Открытий» и вписывайте полученные ответы в заготовленный Бланк ответов, который находится у вас на столах. Время на выполнение работы 5 минут. (Слайды 13-16)
— Время прошло. Надеюсь, что вы справились с заданием. Поменяйтесь бланками ответов со своим соседом. Теперь сверьте результаты с правильными ответами. (Слайд 17)
— Кто справился со всеми пятью задачами? — У кого 4 верных ответа? — Молодцы! — Наш урок подходит к концу. (Слайд 18) Запишем домашнее задание. Пункт 62 страница 146, прочитать; выучить конспект; страница 160 №8 (устно); №564, 566; на дополнительную отметку №567.
— Подведём итоги работы. Мне хотелось бы услышать ваше впечатление об уроке.
Закончите фразу: Сегодня на уроке я…….
— Сегодня на уроке я осталась довольна тем, мы смогли вместе сами открыть новое понятие – средняя линия треугольника и доказать свойство связанное с этим понятием. — Мы с вами молодцы. — Урок окончен.
|
Формулируют признаки параллельности прямых.
— Два угла одного треугольника соответственно равны двум углам другого треугольника.
— Рисунок № 3. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Контролируют ответы друг друга.
Вписывают выбранный ответ на место пропусков в карточке.
—Две стороны.
—Медианы, биссектрисы и высоты треугольника. —Три
—В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения так же пересекаются в одной точке.
—В каждом треугольнике проведён отрезок.
Отвечают хором: соединяет……
Отвечают хором: делит …….
—Соединят середину одной стороны с серединой другой стороны.
Записывают тему урока: «Средняя линия треугольника». Выполняют чертёж. Записывают определение средней линии треугольника.
—Нет.
—Мы не знаем, как найти длины сторон треугольника MNK.
—Треугольники подобны по второму признаку подобия треугольников, т.к. 1)Угол В— общий угол; 2) 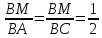 . . —В подобных треугольниках сходственные стороны пропорциональны, а соответственные углы равны. Значит, угол BMN равен углу ВАС. Это равные соответственные углы, образованные прямыми MN и AC и секущей АВ. По второму признаку параллельности прямых следует, что MN׀׀ AC.
Записывают полученный факт. Доказать: 1) MN׀׀ AC
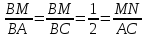
Из равенства 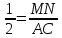 следует, что MN = следует, что MN =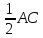
Записывают полученный факт. Доказать: 2) MN =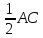
Пытаются формулировать теорему о средней линии треугольника.
По учебнику прочитывают формулировку теоремы.
Один ученик работает у доски, остальные записывают решение задачи в тетрадь «Открытий».
Один ученик работает у доски, остальные записывают решение задачи в тетрадь «Открытий».
Выполняют решения задач в тетради «Открытий» со Слайдов 13-16.
Ученики проводят взаимопроверку полученных результатов.
Записывают домашнее задание в дневник.
Учащиеся проводят самоанализ собственной деятельности. |
Учитель записывает доказательство на доске. Учащиеся работают на заготовленных распечатках.
Учащиеся самостоятельно решают типовые задачи. Ученикам выдаются бланки ответов. По окончании работы проводится взаимопроверка. Слайд 17 содержит ответы на задачи, предложенные ученикам.
Учитель комментирует домашнее задание.
Учащимся необходимо выразить в слове результат и способы достижения. |
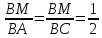 .
.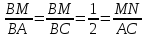
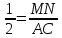 следует, что MN =
следует, что MN =