Данная презентация предназначена для изучения и закрепления теоретического материала по теме “Размещение двух плоскостей в пространстве”, с особым акцентом на признак параллельности плоскостей. Презентация поможет учащимся старших классов средней школы, студентов начальных курсов технических/математических специальностей наглядно понять различные варианты взаимного расположения плоскостей и освоить ключевой критерий их параллельности.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
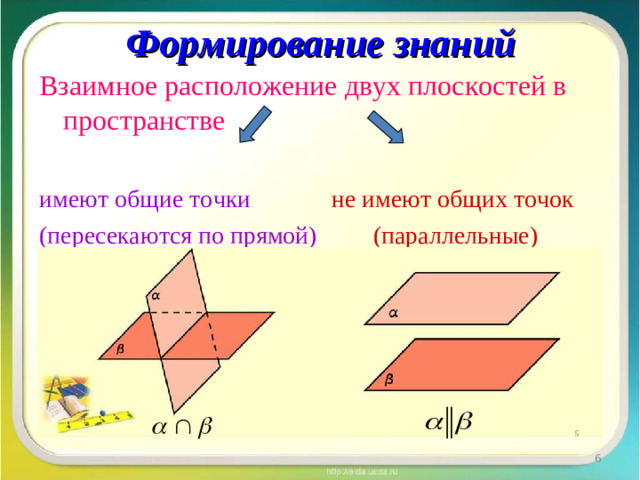
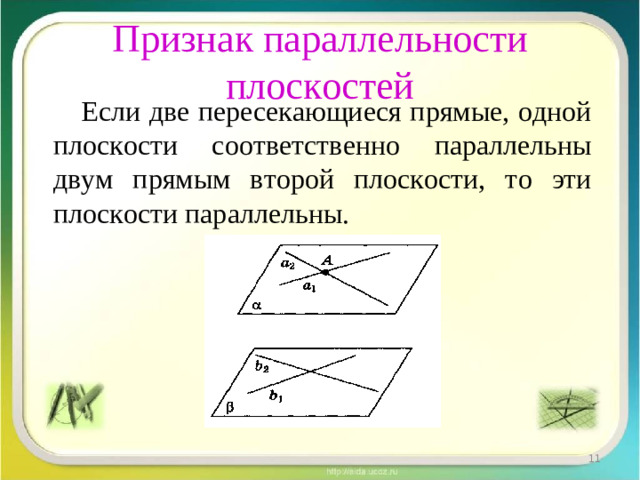
Размещение двух плоскостей в пространстве. Признак параллельности плоскостей
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Размещение двух плоскостей в пространстве. Признак параллельности плоскостей»
Полезное для учителя
Распродажа видеоуроков!
1930 руб.
2760 руб.
1970 руб.
2820 руб.
2160 руб.
3080 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства






















![Домашнее задание [ 1 ] : Выучить таблицу, признак параллельности плоскостей; [2] : § 3 п.10 ,№ №52-55 .](https://fsd.kopilkaurokov.ru/up/html/2025/11/28/k_6929861d0a9fe/img_user_file_6929861ebe1e8_26.jpg)

















