Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Данное интерактивное пособие охватывает практически весь набор прототипов задания 16 («Треугольники и их элементы»). Решения задач разбиты на отдельные ШАГИ, при использовании которых компьютер выдаёт «всплывающие» подсказки, теоремы, формулы, которые учащийся может использовать, а может решать задачу самостоятельно, минуя их.
Через каждые три разобранных задачи учащимся предлагается набор таких же по типу задач для закрепления изученного.
Интерактивное пособие для подготовки учащихся к ОГЭ (раздел «Геометрия»)
Задание 16
«Треугольники»
Учитель математики МОУ СОШ №3 г. Хвалынска
Грибанова Татьяна Алексеевна
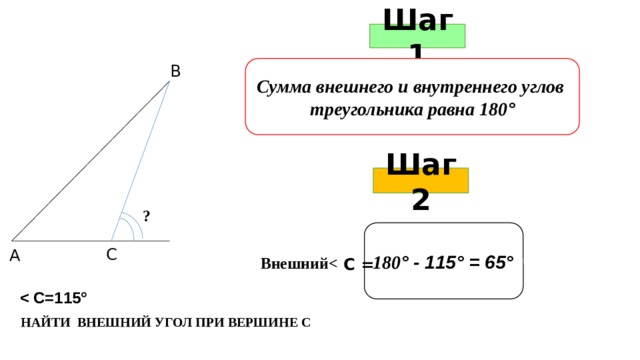
Шаг 1
В
Сумма внешнего и внутреннего углов треугольника равна 180 °
Шаг 2
?
180 ° - 115° = 65°
С
А
Внешний
С =
НАЙТИ ВНЕШНИЙ УГОЛ ПРИ ВЕРШИНЕ С
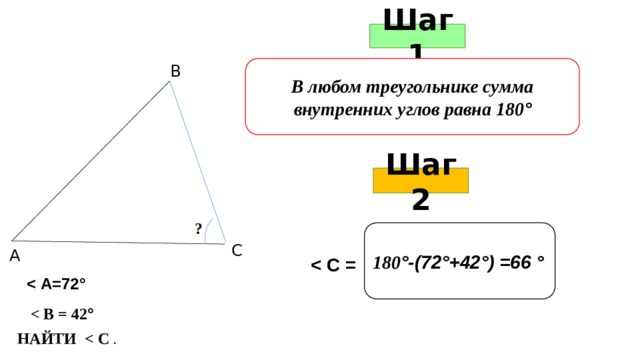
Шаг 1
В любом треугольнике сумма внутренних углов равна 180 °
В
Шаг 2
?
180 °-(72°+42°) =66 °
С
А
°
НАЙТИ .
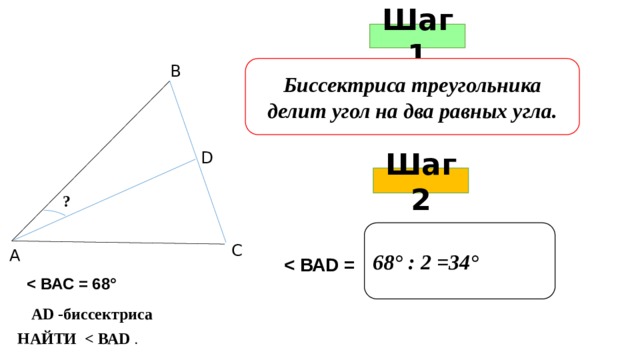
Шаг 1
В
Биссектриса треугольника делит угол на два равных угла.
D
Шаг 2
?
68° : 2 =34°
С
А
АD -биссектриса
НАЙТИ .
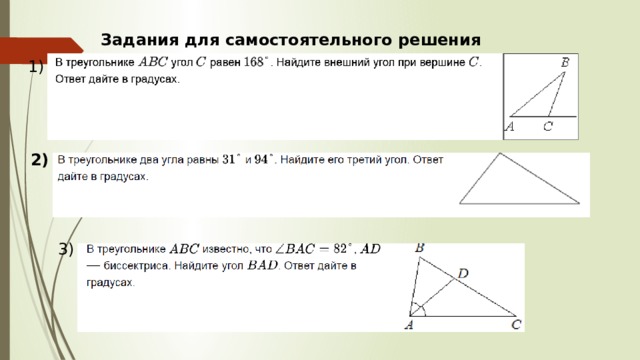
Задания для самостоятельного решения
1)
2)
3)
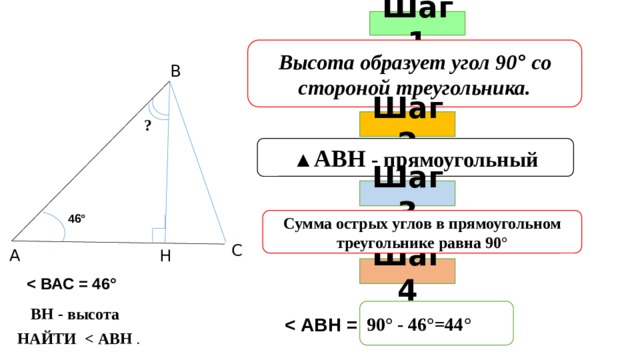
Шаг 1
Высота образует угол 90 ° со стороной треугольника.
В
Шаг 2
?
▲ АВН - прямоугольный
Шаг 3
46°
Сумма острых углов в прямоугольном треугольнике равна 90°
С
А
Н
Шаг 4
90° - 46°=44°
ВН - высота
НАЙТИ .
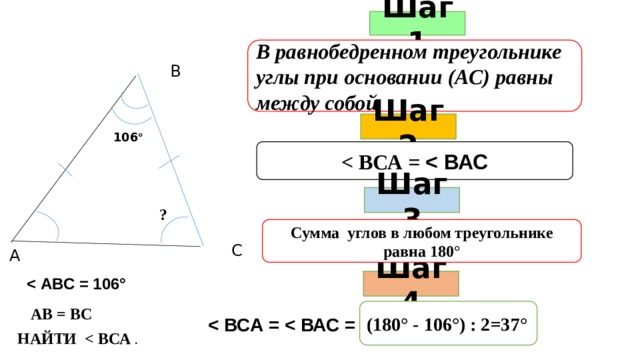
Шаг 1
В равнобедренном треугольнике углы при основании (АС) равны между собой
В
Шаг 2
106 °
Шаг 3
?
Сумма углов в любом треугольнике равна 180°
С
А
Шаг 4
АВ = ВС
(180° - 106°) : 2=37°
НАЙТИ .
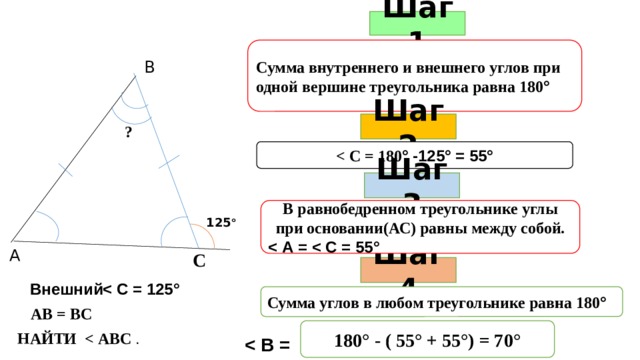
Шаг 1
Сумма внутреннего и внешнего углов при одной вершине треугольника равна 180 °
В
Шаг 2
?
° -125° = 55°
Шаг 3
В равнобедренном треугольнике углы при основании(АС) равны между собой.
125 °
А
С
Шаг 4
Внешний
Сумма углов в любом треугольнике равна 180 °
АВ = ВС
180° - ( 55° + 55°) = 70°
НАЙТИ .
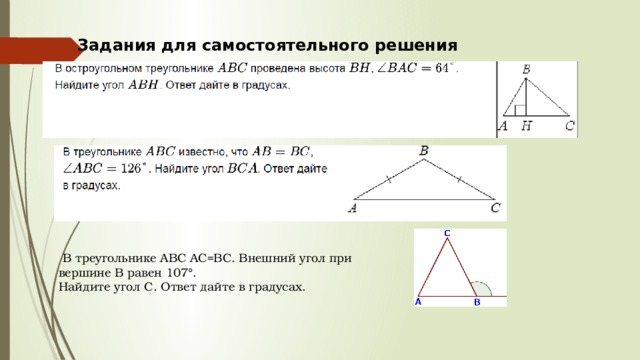
Задания для самостоятельного решения
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 107°.
Найдите угол C. Ответ дайте в градусах.
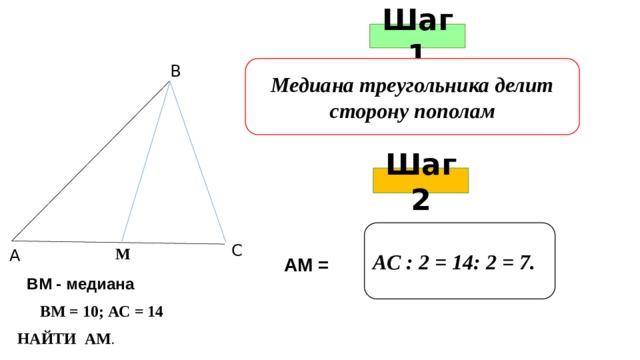
Шаг 1
Медиана треугольника делит сторону пополам
В
Шаг 2
АС : 2 = 14: 2 = 7.
С
М
А
АМ =
ВМ - медиана
ВМ = 10; АС = 14
НАЙТИ АМ .
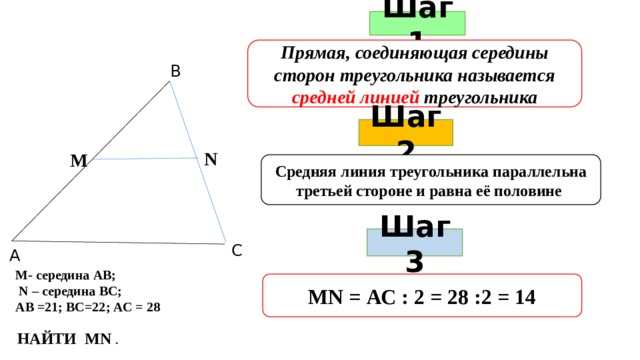
Шаг 1
Прямая, соединяющая середины сторон треугольника называется средней линией треугольника
В
Шаг 2
N
М
Средняя линия треугольника параллельна третьей стороне и равна её половине
Шаг 3
С
А
М- середина АВ;
N – середина ВС;
АВ =21; ВС=22; АС = 28
МN = АС : 2 = 28 :2 = 14
НАЙТИ МN .
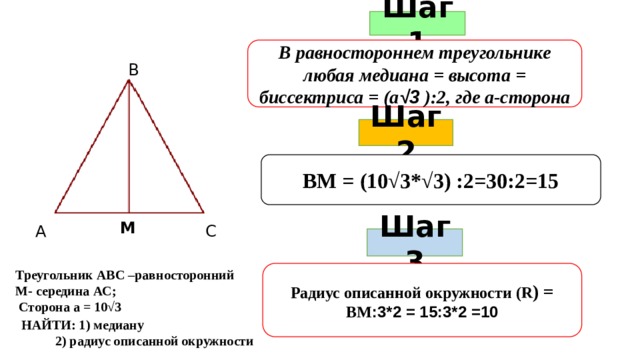
Шаг 1
В равностороннем треугольнике любая медиана = высота = биссектриса = (а √3 ):2, где а-сторона
В
Шаг 2
ВМ = (10√3*√3) :2=30:2=15
М
С
А
Шаг 3
Радиус описанной окружности (R ) = ВМ :3*2 = 15:3*2 =10
Треугольник АВС –равносторонний
М- середина АС;
Сторона а = 10√3
НАЙТИ: 1) медиану
2) радиус описанной окружности
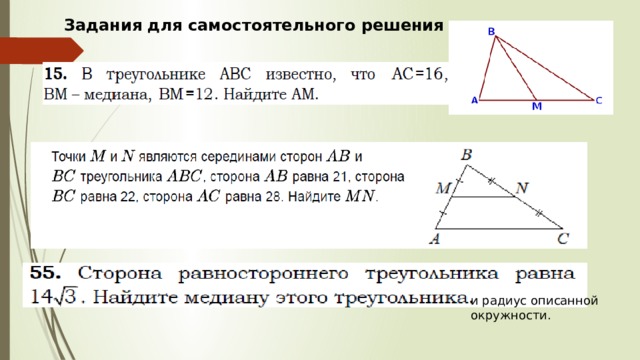
Задания для самостоятельного решения
и радиус описанной окружности.
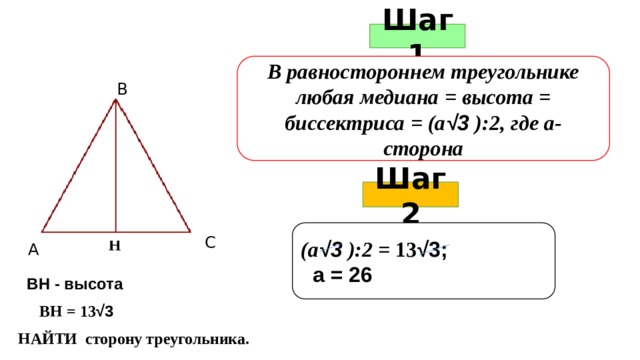
Шаг 1
В равностороннем треугольнике любая медиана = высота = биссектриса = (а √3 ):2, где а-сторона
В
Шаг 2
(а √3 ):2 = 13 √3;
а = 26
С
Н
А
ВН - высота
ВН = 13 √3
НАЙТИ сторону треугольника.
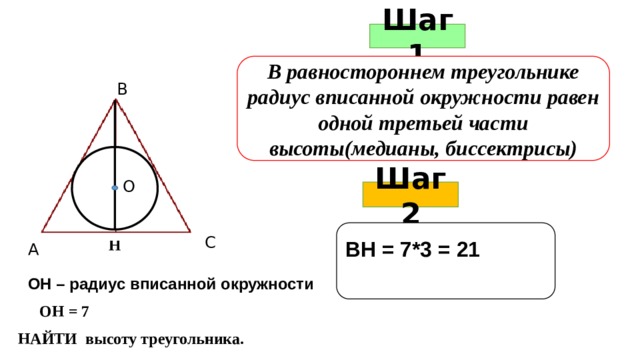
Шаг 1
В равностороннем треугольнике радиус вписанной окружности равен одной третьей части высоты(медианы, биссектрисы)
В
О
Шаг 2
ВН = 7*3 = 21
С
Н
А
ОН – радиус вписанной окружности
ОН = 7
НАЙТИ высоту треугольника.
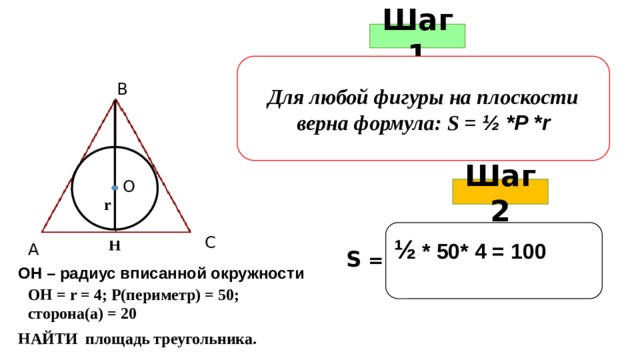
Шаг 1
Для любой фигуры на плоскости верна формула: S = ½ *P *r
В
О
Шаг 2
r
½ * 50* 4 = 100
С
Н
А
S =
ОН – радиус вписанной окружности
ОН = r = 4; Р(периметр) = 50; сторона(а) = 20
НАЙТИ площадь треугольника.
Задания для самостоятельного решения
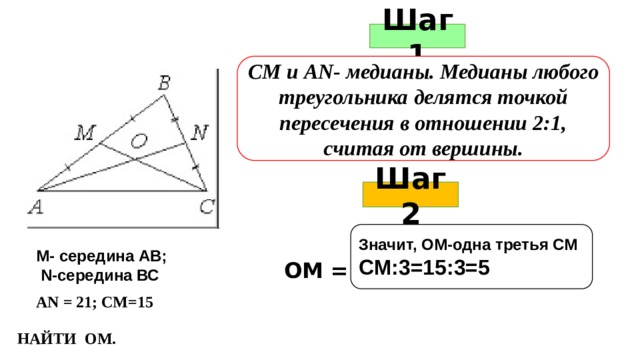
Шаг 1
СМ и АN- медианы. Медианы любого треугольника делятся точкой пересечения в отношении 2:1, считая от вершины.
Шаг 2
Значит, ОМ-одна третья СМ
СМ:3=15:3=5
М- середина АВ;
N-середина ВС
ОМ =
АN = 21; СМ=15
НАЙТИ ОМ.
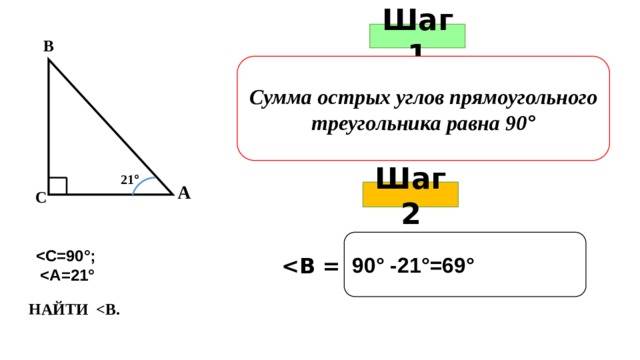
Шаг 1
В
Сумма острых углов прямоугольного треугольника равна 90 °
21 °
А
Шаг 2
С
90° -21°=69°
НАЙТИ
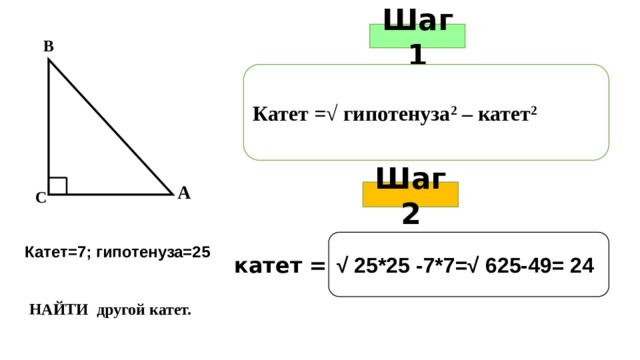
Шаг 1
В
Катет =√ гипотенуза 2 – катет 2
А
Шаг 2
С
Катет=7; гипотенуза=25
√ 25*25 -7*7=√ 625-49= 24
катет =
НАЙТИ другой катет.
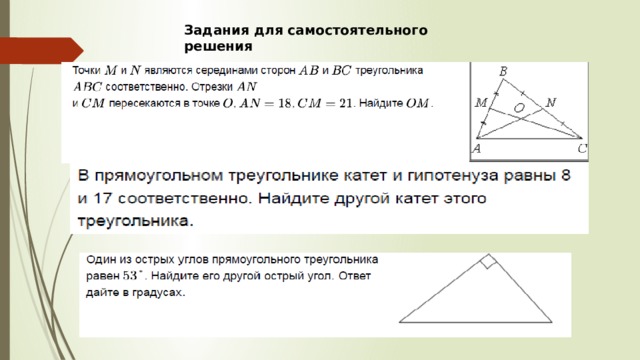
Задания для самостоятельного решения
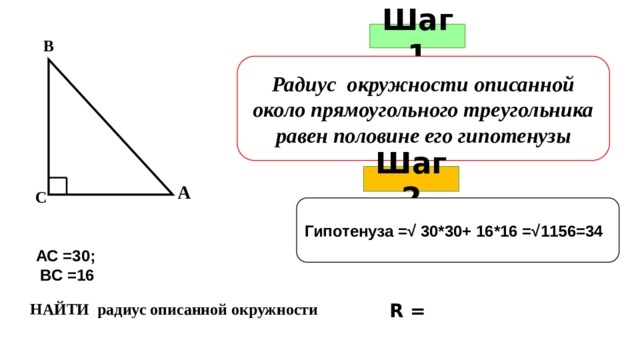
Шаг 1
В
Радиус окружности описанной около прямоугольного треугольника равен половине его гипотенузы
Шаг 2
А
С
Гипотенуза =√ 30*30+ 16*16 =√1156=34
АС =30;
ВС =16
НАЙТИ радиус описанной окружности
R =
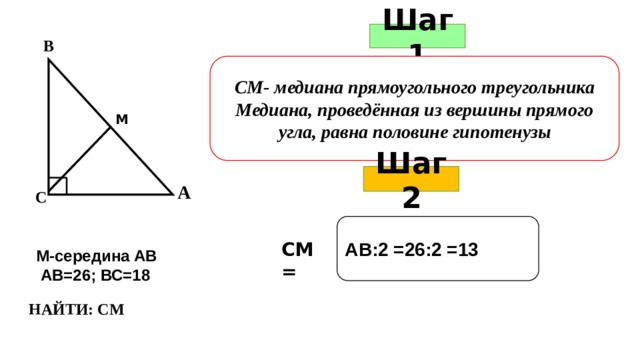
Шаг 1
В
СМ- медиана прямоугольного треугольника
Медиана, проведённая из вершины прямого угла, равна половине гипотенузы
М
Шаг 2
А
С
АВ:2 =26:2 =13
СМ =
М-середина АВ
АВ=26; ВС=18
НАЙТИ: СМ
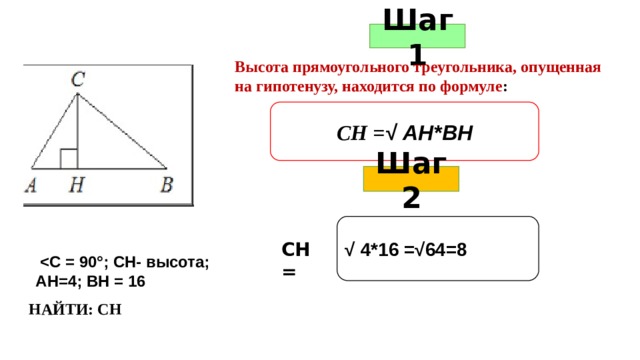
Шаг 1
Высота прямоугольного треугольника, опущенная на гипотенузу, находится по формуле :
СН = √ АН*ВН
Шаг 2
√ 4*16 =√64=8
АН=4; ВН = 16
СН =
НАЙТИ: СН
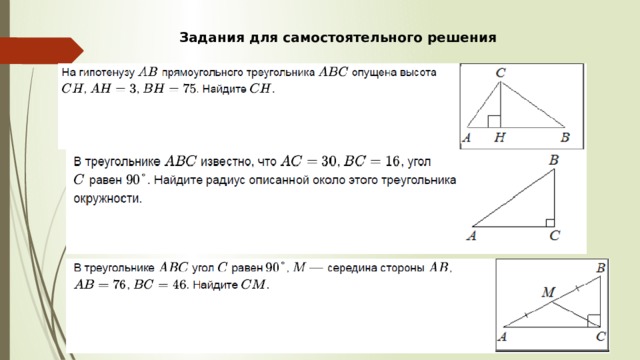
Задания для самостоятельного решения
Использованные материалы
1. Задачи Открытого банка ОГЭ сайта ФИПИ; http://oge.fipi.ru/os/xmodules/qprint/index.php?proj=DE0E276E497AB3784C3FC4CC20248DC0
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
