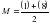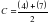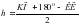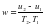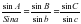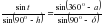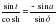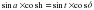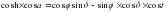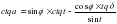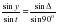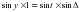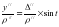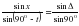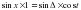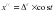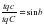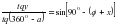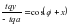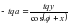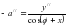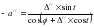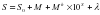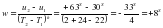| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН КОЛЛЕДЖ ГЕОДЕЗИИ И КАРТОГРАФИИ

Предмет: Геодезия Раздел: Автономные методы определения Тема: Определение азимута астрономическим методом Преподаватель Федорук Е.К.
г. Семей 2015-2016 г.
9.1 Теория и сущность определения азимута.
1.Назначение астрономических определений в топографо-геодезическом производстве. При построении съемочной сети приходится определять истинный азимут астрономическим методом. Необходимость в определении астрономических азимутов при создании съемочных геодезических сетей обычно обуславливается недостаточной плотностью исходных пунктов геодезической сети, отсутствием видимости на смежные пункты триангуляции или утратой знаков на некоторых из них. Такая необходимость возникает: Астрономический азимут определяют по наблюдениям небесных светил (Солнца и звезд), а от него переходят к геодезическому азимуту, используя вычисленные значения геодезического азимута, по формулам переходят к дирекционному углу ориентирного направления. Астрономический метод определения азимутов направлений является автономным, и не зависит от наличия на местности пунктов геодезической сети. Точность определения астрономического азимута обусловлена его назначением. Наиболее точные азимутальные определения (0,5") выполняют на пунктах государственной геодезической сети (пунктах Лапласа), с погрешностью порядка 5 - 7" определяют астрономические азимуты в сетях триангуляции и полигонометрии при привязке ориентирных пунктов. Чаще всего астрономические определения азимутов осуществляются при развитии и ориентировании съемочных сетей; в этом случае эти определения носят приближенный характер, а требуемая точность не превышает 30 - 60". В программе курса геодезии рассматривается теория и практика приближенных способов определения астрономического азимута, когда в качестве объектов наблюдения используют легко отыскиваемые на небосводе светила - Солнце и Полярная звезда.
2. Основные понятия и формулы сферической тригонометрии: сферический треугольник и его элементы, формулы косинусов и синусов, четырех и пяти элементов, формулы прямоугольного сферического треугольника..
При определении астрономического азимута, определении широты, долготы пунктов опираются на решение сферических треугольников. 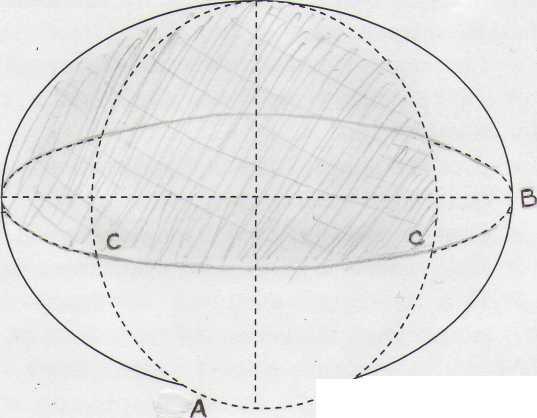 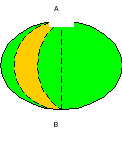
Сферический двуугольник АВ; Сферический треугольник АВС. Две стороны (дуги по 1800), Углы А;В;С; стороны а, в, с; Два сферических угла. Сферический треугольник решается по трем известным элементам. Если один из его углов равен 90°, то такой сферический треугольник называется прямоугольным и для его решения достаточно знать два каких-либо элемента.
Формулы для решения сферических треугольников, используемые при определении астрономического азимута: Косинус любой стороны сферического треугольника равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними. cos a = cosb*cosc +sinb*sinc*cos A Произведение котангенса крайней стороны на синус внутренней стороны равно произведению котангенса крайнего угла на синус внутреннего угла плюс произведение косинусов внутренних элементов ctg a*sin с = ctgA sin В + cos B* cos с
Формула прямоугольного сферического треугольника:
Правило Непера: косинус любого элемента прямоугольного сферического треугольника равен произведению котангенсов смежных с ним элементов cos C = ctgb* ctg (90° - а) ; cos b=ctgA* ctg С;
3. Сущность определения астрономического азимута. Переход от азимута к дирекционному углу.

На рисунке изображены направление меридиана в точке О, направление на земной предмет Δ В и направление на небесное светило, в качестве которого может быть выбрана любая яркая звезда или Солнце *δ. Пусть: а - азимут светила ; А - азимут земного предмета; Q - горизонтальный угол между земным предметом и светилом. Из рисунка очевидно, что А = а+ Q
В связи с суточным вращением Земли вокруг своей оси положение светила на небосводе непрерывно меняется, и через некоторый промежуток времени оно займет новое положение. Соответственно этому изменяется азимут светила и горизонтальный угол. Несмотря на это, сумма этих измененных значений азимутов (А) останется прежней, поскольку азимут земного предмета есть величина постоянная. Таким образом, для определения азимута земного предмета необходимо определить азимут светила и измерить горизонтальный угол между светилом и местным предметом в один и тот же момент времени. Угол (Q) измеряется непосредственно с помощью теодолита, величина азимута светила может быть определена косвенным путем - как функция измеренной высоты светила (h) , либо его часового угла (t).
Небесная сфера 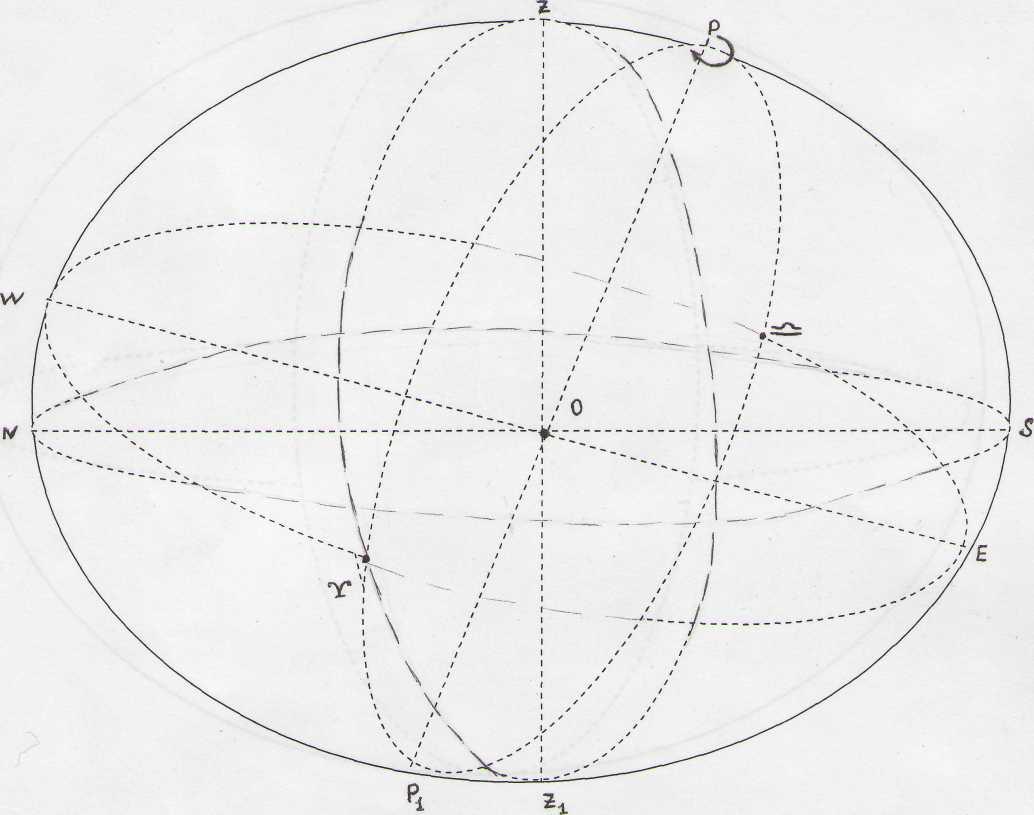 4. Небесная сфера. Основные круги, линии и точки небесной сферы. Для удобства описания небесных явлений, а также математических расчетов, выполняемых при астрономических определениях, пользуются понятием вспомогательная небесная сфера. радиуса с центром в произвольной точке. За центр небесной сферы принимается точка стояния наблюдателя (О). Но поскольку расстояния до светил велики по сравнению с радиусом Земли, за центр, вспомогательной небесной сферы можно принимать любую точку на земной поверхности. Такая условная схема расположения небесных светил соответствует
картине видимого нами звездного неба, хотя истинные расстояния до звезд очень различны, все светила кажутся одинаково удаленными от нас. Точки W и Е пересечения небесного горизонта с первым вертикалом,
называются точками Запада и Востока. Эклиптика это видимый годичный путь Солнца по небесной сфере.
Эклиптика составляет угол 23°27” с плоскостью небесного экватора. Точками
весеннего и осеннего равноденствия называются точки пересечения небесного
экватора дважды в год Солнцем. Точка весеннего равноденствия обозначается знаком γ, и проходит под созвездием Овна. 5. Системы координат небесных светил: горизонтальная, 1 и 2 экваториальные. В астрономии для определения положения небесных светил пользуются тремя различными системами координат: горизонтальной, первой экваториальной и второй экваториальной. Они отличаются друг от друга положением больших кругов, принимаемых за начальные.
Горизонтальная система координат. Основными координатными кругами в этой системе служат небесный горизонт и меридиан наблюдателя. Положение светила определяется координатами: азимут светила (а) и высота светила (h). h - высота светила, измеряется отрезком дуги вертикала (круга высот) и может иметь значение от 0°до 90°. Z — зенитное расстояние светила. h + Z = 90° Азимутом светила называют дугу небесного горизонта от точки юга до вертикала светила, или двухгранный угол между плоскость меридиана и плоскостью вертикала проходящего через светило, или сферический угол в точке Z между дугой меридиана и дугой вертикала светила. В астрономии принято отсчитывать азимуты от южной части меридиана наблюдателя (точки юга S), но для удобства пользования астрономических азимутов в геодезических целях его отсчитывают от северной части меридиана (точки N) в направлении часовой стрелки, в пределах 00 — 3600 . Для данной точки наблюдения значение азимута и высоты светила будут различны в разное время суток и их следует относить к определенному моменту времени измерений. В разных точках земной поверхности отвесная линия имеет разное направление, поэтому в один и тот же момент времени, но для различных точек наблюдений, горизонтальные координаты а и h одного и того же светила также не будут одинаковы.
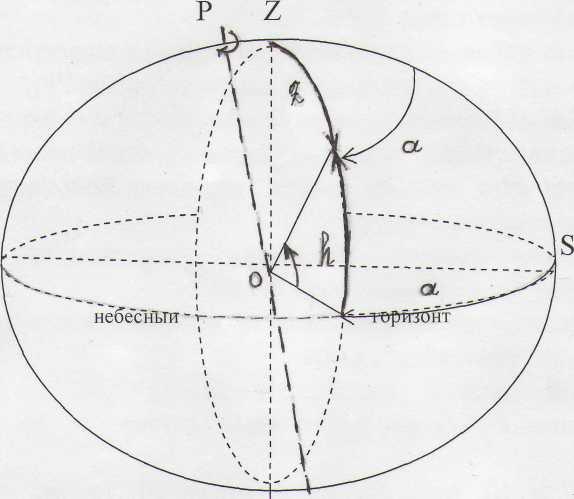
Первая экваториальная система координат. Эта система сходна с системой географических координат на земной поверхности. Положение светила определяется координатами: склонением светила δ, и часовым углом t. В этой системе координат отсчитывают от небесного экватора и по небесному экватору.
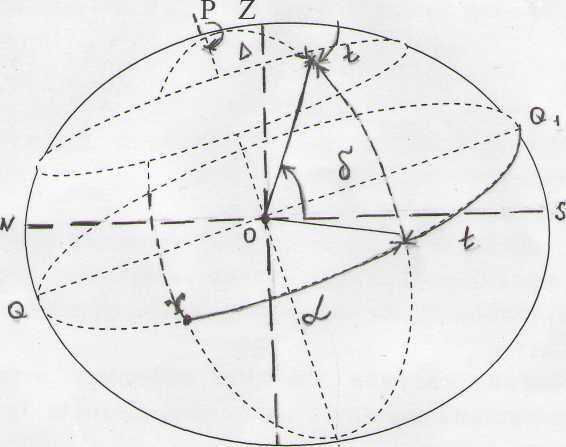
В северном полушарии небесной сферы склонение светила считаются положительными, а в южном полушарии – отрицательными. δ - склонение светила может изменяться от 0° до 90°. В любой точке небесного экватора, значение δ равно 0°, а для северного и южного полюсов соответственно - +900; и —900 . В процессе суточного движения светило перемещается по суточной параллели gg1 все точки, которой находятся на одинаковом расстоянии от небесного экватора, равным его склонению, поэтому для звезд δ не зависит от суточного движения небесной сферы и является постоянной величиной. Значения склонений для различных светил определяются из наблюдений на обсерваториях и публикуются в специальных астрономических таблицах - Астрономическом Ежегоднике или Каталоге координат Солнца и ярких звезд.
Полярным расстоянием называют дугу круга склонений от полюса до светила. Δ — полярное расстояние. δ +Δ = 90° Часовым углом светила называют дугу небесного экватора от плоскости меридиана до круга склонений светила, или двухгранный угол заключенный между плоскостью меридиана и плоскостью круга склонений светила, или сферический угол при точке Р между дугой меридиана и дугой круга склонений светила. t - часовой угол. Название «часовой угол» объясняется тем, что при вращении Земли вокруг своей оси его величина изменяется пропорционально времени. Поэтому часовой угол принято выражать как в угловой (от 0° до 360°), так и в часовой мере (от 0hдо 24h). Так как полный оборот светила в 360°соответствует 24h, то lh=15° lm=15/ ls= 15" Этими соотношениями пользуются на практике для перевода углов, выраженных в угловой мере, в часовую и обратно. Вторая экваториальная система координат. В этой системе координат основными кругами являются небесный экватор и круг склонений, проходящий через точку весеннего равноденствия у, положение светила определяются координатами: склонением δ и прямым восхождением светила а. α —прямое восхождение светила, выражается всегда в часовой мере от 0 до 24 Так как точка весеннего равноденствия γ, как и все светила, участвует в суточном вращении небесной сферы, координата α (прямое восхождение) для данного светила всегда постоянна, и подобно склонению δ не зависит от положения наблюдателя на земной поверхности. В астрономических таблицах в качестве исходных данных для различных астрономических определений приводятся значения прямого восхождения α, и склонения δ Солнца и ярких звезд. 7. Измерение времени. Суточное движение и кульминация светила. Звездные сутки и звездное время. Истинные солнечные сутки и солнечное время, средние сутки и среднее время. Уравнение времени. Тропический год. Соотношение между продолжительностью звездных и средних суток. Время всемирное, местное, поясное, декретное. Астрономический Ежегодник и Астрономический каталог. С течением времени значение небесных координат a, h, t непрерывно меняется, поэтому при их определениях возникает необходимость фиксировать момент наблюдений, иначе говоря - измерять время. Время может быть измерено с помощью таких периодических явлений, которые в природе повторяются многократно и с одинаковой продолжительностью. К таким явлениям относятся годичный оборот Земли вокруг Солнца и суточный оборот Земли вокруг своей оси. Таким образом, в качестве единиц измерения времени сама природа предоставила нам год и сутки. Доли суток - часы, минуты, секунды - измеряются специальными механическими, электронными и атомными приборами- часами и хронометрами. В зависимости от выбранной единицы измерения времени в астрономии используются различные системы его счета, а именно, звездное и солнечное время. В обиходе пользуются солнечным временем, которое, в свою очередь, подразделяется на местное, поясное, всемирное и декретное; все они различаются между собой принятым началом отсчета. Единицей измерения звездного времени являются звездные сутки -период одного полного оборота Земли вокруг своей оси. За начало счета звездных суток принят момент верхней кульминации точки весеннего равноденствия γ. Звездные сутки это промежуток времени между двумя последовательными верхними кульминациями точки весеннего равноденствия в меридиане места наблюдения. По сравнению с солнечными, звездные сутки - наиболее точная и легко проверяемая постоянная единица измерения времени, поскольку видимое движение звезд происходит с постоянной скоростью. Она делится на 24 звездных часа, звездный час - на 60 звездных минут, минута - на 60 звездных секунд. Промежуток времени, считаемый от момента верхней кульминации точки весеннего равноденствия до данного момента и выраженный долях звездных суток (часах, минутах и секундах), называется звездным временем. Звездным временем S удобно пользоваться при определениях координат небесных светил: часовых углов звезд и их прямого восхождения. Для любой точки земной поверхности звездное время численно равно часовому углу точки весеннего равноденствия S = t r или сумме прямого восхождения любого светила а и его часового угла t S = α + t (1) В момент верхней кульминации светила его часовой - угол равен нулю, поэтому звездное время равно его прямому восхождению, т.е. S = α (2) При определении азимута светила решают обратную задачу, вычисляя часовой угол по известному звездному времени и прямому восхождению, т.е. t = S - α (3) Истинное солнечное время. Применяемое в астрономии звездное время не используется в обычной жизни, так как распределение времени в быту связанно со сменой дня и ночи, а следовательно зависит от положения Солнца на небосводе. Поэтому в обиходе пользуются не звездным временем, а солнечным временем. Различают два вида солнечного времени: истинное и среднее. Истинными солнечными сутками называется промежуток времени между двумя последовательными нижними кульминациями центра истинного (непосредственно видимого) Солнца в меридиане места наблюдения. Момент нижней кульминации истинного Солнца принят за начало солнечных суток и называется истинной полночью.
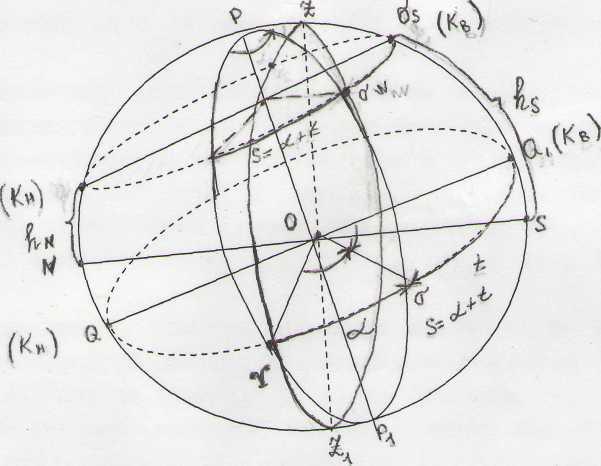
Период между истинной полночью и данным моментом времени называется истинным солнечным временем, обозначается m0 , и измеряется часовым углом Солнца t0 . Поскольку за начало счета часовых углов светил приняты моменты их верхних кульминаций, истинное солнечное время в данный момент будет отличаться от часового истинного Солнца на 12 часов. m0 = t0 + 12 h (4) В астрономии истинное солнечное время используется при определении азимутов направлений по наблюдениям Солнца. В отличии от видимого движения звезд, вращающихся с постоянной скоростью по одним и тем же суточным параллелям, видимое годичное движение Солнца происходит не по экватору, а по эклиптике, наклоненной к плоскости экватора, в направлении, обратном суточном вращению небесной сферы. Скорость этого видимого движения не постоянна, так как с приближением Земли к Солнцу, расположенному в одном из фокусов земной орбиты, скорость движения Земли возрастает из-за увеличения силы их взаимного притяжения. Наоборот, с уменьшением этой силы скорость движения Земли уменьшается (закон Кеплера). В результате одну половину эклиптики, расположенную выше небесного экватора, Солнце проходит за 186 суток (с 21 марта до 23 сентября), а вторую половину, расположенную ниже экватора, - за 179 суток. Поэтому продолжительность истинных солнечных суток в различное время года не одинакова. Среднее солнечное время. Для удобства пользования солнечным временем в обычной жизни введено среднее солнечное время, отсчитываемое от «среднего Солнца». Среднее Солнце это воображаемая точка, которая равномерно движется по экватору в том же направлении, что и перемещающееся по эклиптике истинное Солнце. Средне Солнце совершает свой годичный путь за то же время, за какое истинное Солнце проходит эклиптику. Средними солнечными сутками называется промежуток времени между двумя последовательными нижними кульминациями среднего Солнца. Продолжительность их равна средней за год продолжительности истинных солнечных суток. Подобно звездным, средние солнечные сутки делятся на 24 средних часа, 1 средний час - на 60 минут, 1 средняя минута - на 60 секунд. Поскольку среднее время течет равномерно, то его можно измерять при помощи часов, что удобно в быту. Численной мерой среднего солнечного времени m служит часовой угол tm среднего Солнца, увеличенный на 12 h. m = tm+12h (5) Уравнением времени называется разность т| между истинным и средним солнечным временем. η = т0 - т (6) Из равенства 4 и 5 следует, что уравнение времени равно также разности часовых углов истинного и среднего Солнца. η = t0 - tm. Поэтому уравнение времени используют для вычисления часового угла Солнца при определениях азимута. Величина η+ 121, рассчитанная на начало каждой календарной даты для Гринвичского меридиана, приводится в таблице «Солнце» Астрономического Ежегодника или Каталога координат Солнца и ярких звезд. Максимальное значение разности η достигает величины 16,5'. Соотношение между звездным и солнечным временем. Исходной единицей для измерения времени в астрономии является тропический год. Тропическим годом называется промежуток времени между двумя последовательными прохождениями среднего или истинного Солнца через точку весеннего равноденствия.
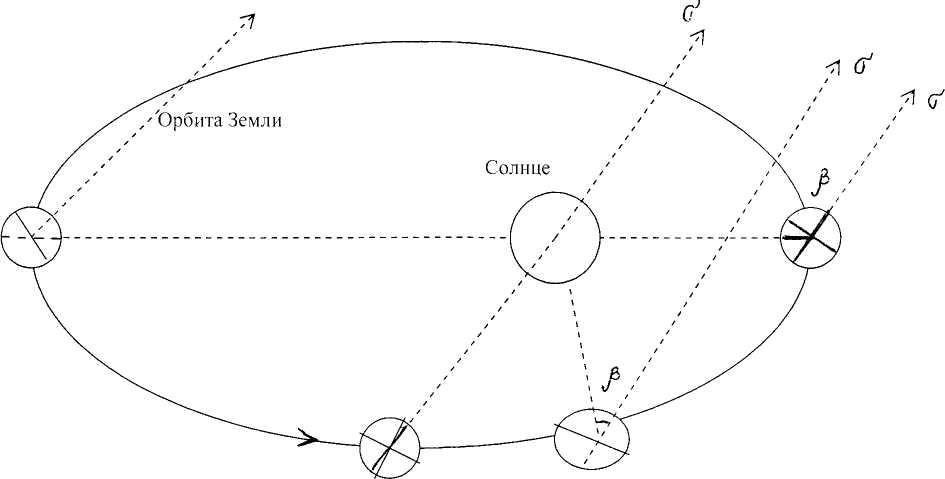
Из астрономических наблюдений установлено, что за один год Земля совершает 366,2422 полных оборота вокруг своей оси, следовательно, один тропический год содержит это же число звездных суток. Но вследствие обращения Земли вокруг Солнца (т.е. вследствие годичного его движения) число солнечных суток в тропическом году составляет 365,2422, т.е. на одни сутки меньше, чем звездных. Рассмотрим это на рисунке.  Направление движения Земли Допустим, что в какой - либо момент времени точка весеннего равноденствия γ и среднее Солнце С кульминируют одновременно, это значит, что начало звездных суток совпадает с началом средних солнечных. После того как небесная сфера сделает полный оборот, закончатся звездные сутки. Однако за это время Земля успевает переместится вправо по своей орбите (из-за вращения вокруг Солнца) в направлении, обратном суточному вращению. Следовательно, момент кульминации Солнца отстанет от точки весеннего равноденствия на некоторый угол β, равный примерно 1 °, так как
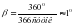
В каждые из последующих суток Солнце все больше и больше будет отставать от кульминации точки весеннего равноденствия. За весь год этот угол отставания составит 360°. Это значит, что за один год Солнце будет иметь на одну кульминацию (т.е. на одни сутки) меньше, чем точка весеннего равноденствия. Таким образом:
1 год = 366,2422 звездных суток = 365,2422 средних солнечных суток.
Следовательно,
1 средние сутки = 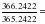 звездных суток = звездных суток = 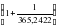 звездных суток звездных суток или 1 средние сутки = 1 звездным суткам +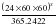 = 1 звездным суткам + 3m 57S = 1 звездным суткам + 3m 57S Приближенно 1 средние сутки = 1 звездным суткам +4 m По аналогии 1 средний час = 1 звездному часу + 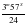 ; ; 1 средний час = 1 звездному часу + 9,856 S ≈ 1 звездному часу +10 S
В последнем соотношении член 9,856S или приблизительно 10S, обозначаемый буквой µ , представляет собой разность между одним звездным и одним солнечным часом и служит коэффициентом для перевода среднего времени в единицы звездного времени. µ ≈ 9,856 S ≈ 10 S - коэффициент для перевода среднего времени в единицы звездного времени.
В общем виде связь между звездным и средним солнечным временем выражается формулой:
Местное, поясное, всемирное и декретное время. В зависимости от выбора начала отсчета времени различают: Местное поясное время Т; Всемирное время Т0; Декретное время D; Поскольку измерение солнечного и звездного времени связано с часовыми углами, которые отсчитываются от меридиана места наблюдения, то часовые углы светила на любом географическом меридиане в один и тот же момент времени будут различны, а поэтому будет и свое местное время. Таким образом, часовые углы точки весеннего равноденствия, истинного и среднего Солнца, отсчитанные от моментов их кульминаций на меридиане места наблюдения, называются соответственно
Небесная сфера
Из рисунка видно, что в двух точках земной поверхности 1 и 2, лежащих на разных меридианах разность одноименных местных времен будет равна разности долгот этих точек. Например: S2 – S1 = λ 2 - λ 1
m2 – m 1 = λ 2 - λ 1
При решении различных задач практической астрономии (определение времени, часовых углов светил) значение долгот принято выражать в часовой мере. Использование местного времени в повседневной жизни было бы неудобным. В самом деле, показания часов, в каком либо пункте Земли должны были бы меняться при перемещении наблюдателя в другой пункт, причем это измерение выражалось бы в часах, минутах и секундах, т.е. в дробных долях суток. Чтобы избежать этого неудобства, принято пользоваться поясным временем. С этой целью поверхность земного шара делится меридианами на 24 часовых пояса примерно через 150 по долготе, что соответствует изменению времени в смежных поясах ровно на 1 час. Поясным временем Т – называется, среднее солнечное время, относящееся к среднему меридиану данного часового пояса и распространенное на всю его территорию. Начальным для отсчета всех часовых поясов от 0 до 23 по направлению к востоку принят Гринвичский меридиан, являющийся средним меридианом нулевого часового пояса. Границы часовых поясов проведены с учетом административных границ, крупных рек и железных дорог, несколько отступающих от соответствующих граничных меридианов. При переходе из одного часового пояса в другой поясное время меняется на целое число часов, минуты и секунды остаются прежними. Местное время на Гринвичском меридиане называется всемирным временем и обозначается Т0 и S0. Необходимые для обработки астрономических наблюдений координаты небесных светил - склонение, прямое восхождение, уравнение времени – приводятся в Астрономических таблицах на 0 h всемирного времени, то есть на Гринвичскую полночь. Чтобы пользоваться ими при вычислениях, необходимо предварительно определить всемирное время Т0, соответствующее моменту наблюдений, а затем проинтерполировать на этот момент выбранные на 0 h значения координат или уравнение времени. Всемирное время можно определить путем вычитания из поясного времени Т номера часового пояса, в котором находится пункт наблюдения. Т0 = Т – n Чтобы более полно использовать светлое время суток, в некоторых странах, в том числе и в нашей, показания часов переводят на один час или на 2 часа вперед относительно поясного времени. Такое время D называется декретным. Например в России в летний период поясное время увеличивается на 2 часа, также как и в нашем государстве. D = Т + 2 h И в зимний период – на один час D = Т + 1 h Декретное время второго часового пояса, в котором расположена Москва, называют московским временем. Таким образом, в зависимости от времени года переход от декретного времени к всемирному времени осуществляется по формуле: Т0 = D – (n +2 h) или Т0 = D – (n +1 h) Многообразие видов времени, употребляемого в астрономии и в обиходе, обусловлено необходимостью удовлетворения науки, техники, и организации повседневной жизни людей.
Параллактический (астрономический) треугольник и его элементы. Связь между системами координат. ![]()
Дуги меридиана наблюдателя, круга склонений и вертикала образуют на небесной сфере параллактический (астрономический) треугольник с вершинами в точках: Р (полюс Мира), Z (зенит), δ (светило). Р= 90° - hp = 90° - φ Другой стороной параллактического треугольника является дуга вертикала (круга высот), Z σ, равная зенитному расстоянию светила, или дополнению до 90° его высоты h Z σ= Z = 90° - h Рσ = Δ = 90°-δ Угол при вершине Z равен азимуту а светила, если оно находится в восточной части небесной сферы или его дополнению до 360°, если светило расположено в ее западной части. Угол при вершине Z равен азимуту (а) светила, если оно находится в восточной части небесной сферы или его дополнению до 360°, если светило расположено в ее западной части. Также в зависимости от положения светила на небесной сфере угол при вершине Р может быть равным или часовому углу светила t, или его дополнению до 360 . Третий угол треугольника при вершине σ называется параллактическим углом. Решая по формулам сферической тригонометрии параллактический треугольник, можно определить любой из его элементов, если известны величины трех остальных. Способы определения азимута земного предмета через азимут светила основаны на решении параллактического треугольника, один из элементов которого – высота светила h (или ее дополнение до 90 зенитное расстояние Z) измеряется непосредственно теодолитом. Остальные элементы параллактического треугольника определяются различными методами: Географические координаты точки наблюдения - ее широту φ и долготу λ определяют по топографической карте возможно более крупного масштаба. Склонение светила δ мало изменяющаяся в течении суток экваториальная координата, приводится в Астрономическом Ежегоднике или Каталоге координат Солнца и ярких звезд. Часовой угол t светила находят по результатам определения времени наблюдения с учетом долготы места наблюдения.
Способы определения азимута светила из решения астрономического треугольника. Определение азимута по измеренной высоте светила. В этом случае известными являются: дуга круга склонений, равная полярному расстоянию Δ светила, т.е. дополнению склонения δ до 90°.
Рσ= Δ = 90° - δ. дуга вертикала (круга высот), Zσ, равная зенитному расстоянию светила, или дополнению до 90° его высоты h. Zσ= Z = 90° - h широта точки наблюдения φ
Определение азимута по часовому углу Солнца. Для этого способа определения азимута являются исходными две стороны параллактического треугольника: дуга круга склонений, равная полярному расстоянию Δ светила, т.е. дополнению склонения δ до 90°.
Рσ= Δ = 90° - δ. дуга вертикала (круга высот), Zσ, равная зенитному расстоянию светила, или дополнению до 90° его высоты h. Zσ= Z = 90° - h часовой угол светила t, который находится как функция измеренного времени наблюдения. 6. Параллактический (астрономический) треугольник и его элементы. Связь между системами координат. Способы определения азимута светила из решения астрономического треугольника, зависимость высоты полюса Мира от широты места наблюдения. Связь широты места наблюдения с небесными координатами. Представим Землю и небесную полусферу, видимую из точки М, в которой находится наблюдатель. Широта φ этой точки есть угол между плоскостью земного экватора gg1 и отвесной линией ОМ. Касательная к земной поверхности в точке М плоскость небесного горизонта изобразится прямой линией NS. Линия MP, параллельная оси вращения Земли РР1 представляет собой ось Мира, Плоскость MQ - небесный экватор. Из рисунка видно, что угол NMP1 между осью Мира РР1 и плоскостью небесного горизонта есть высота h p полюса Мира и равен углу MOg, т.е. широте φ точки М (стороны обоих углов взаимно перпендикулярны)
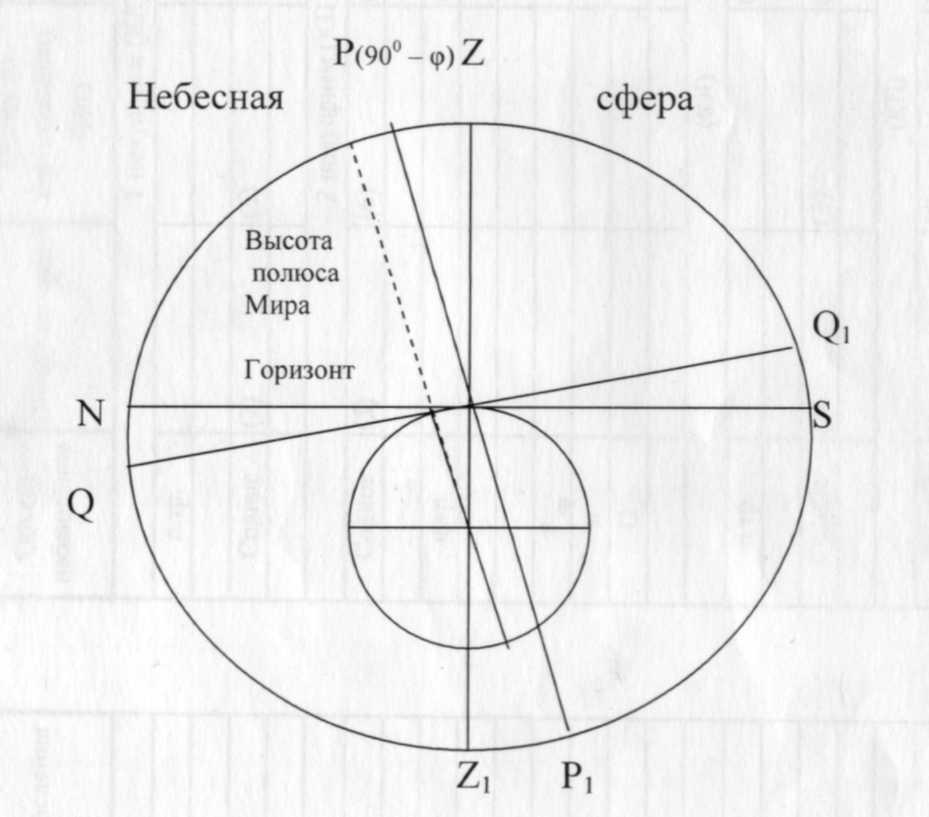
Таким образом, угловая высота полюса Мира над небесным горизонтом равна географической широте места наблюдения, т.е. hр = φ. Следовательно, длина дуги небесного меридиана между полюсом Мира и зенитом будет равна: PZ = (90° - φ) Полученное соотношение широко используется при решении различных задач астрономии. 9.2. Определение азимута по высоте Солнца 8. Астрономическая рефракция, и ее учет. Выгоднейшие условия наблюдения.
Астрономической рефракцией называется явление преломления лучей света, идущих от светила при прохождении ими слоев атмосферы различной плотности. Для пояснения сущности этого явления атмосферу можно представить как совокупность тонких слоев воздуха, плотность которых увеличивается по мере приближения к поверхности Земли. При отсутствии атмосферы наблюдатель, находящийся в некоторой точке М, увидел бы светило σ по направлению Мσ. В действительности, луч света, проходя разные слои атмосферы, будет преломляться на границе этих слоев и представит собой ломанную линию. При бесконечно малых по толщине слоях воздуха эта ломанная линия превратится в кривую. По законам оптики при прохождении луча света от слоев меньшей плотности к слоям большей плотности углы преломления постепенно уменьшаются и выпуклость рефракционной кривой будет всегда обращена в верх. Наблюдатель при этом будет видеть светило по направлению к касательной к этой кривой в точке М, т.е. по направлению Мσ. 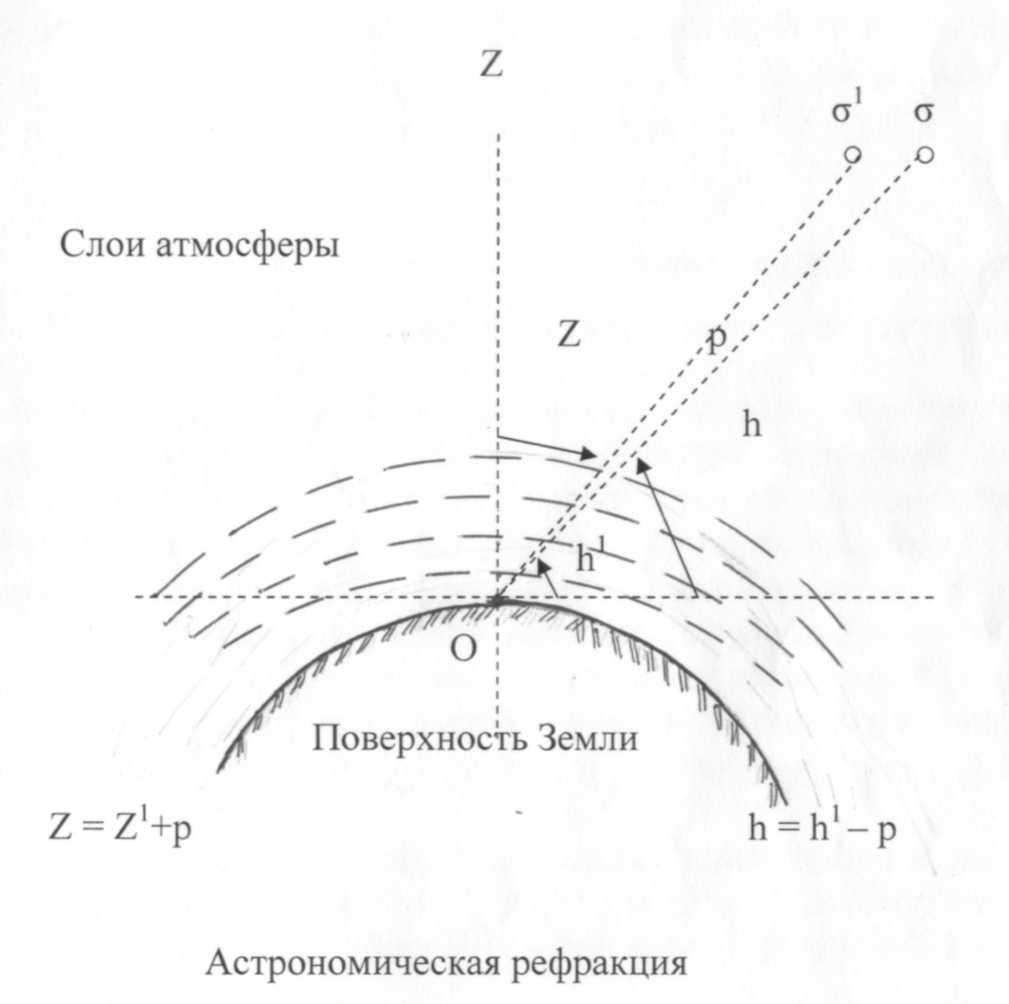
Как видно из рисунка, измеренная высота светила h1 будет больше действительной h на некоторую величину р, называемую поправкой за астрономическую рефракцию. Таким образом, чтобы получить исправленное значение высоты светила нужно ее измеренное значение уменьшить на величину угла р, т.е. h = h' - р. Если вместо высоты h определено зенитное расстояние Z, то его величина, исправленная за влияние астрономической рефракции, будет равна:
Z = Z' +р. Величина поправки за рефракцию р зависит от высоты или зенитного расстояния светила. Поправка за рефракцию увеличивается по мере приближения светила к горизонту и уменьшается до минимума при расположении светила вблизи зенита и в значительной степени обусловлена плотностью атмосферы, которая, в свою очередь, непосредственно связана с температурой и давлением воздуха. Поэтому при измерении вертикальных углов на светило необходимо определять давление и температуру воздуха. В «Астрономическом Ежегоднике» и «Каталоге координат Солнца и ярких звезд» приводятся специальные таблицы для определения средней поправки за рефракцию ро, рассчитанной для нормальных атмосферных условий, т.е. для давления В=760 мм рт. ст. и температуры воздуха t = +10° С. Величину р0 выбирают по аргументу h или Z. Если в момент измерений давление и температура отличались от нормальных в значение р0 вводятся поправки Δ PB и Δ Pi,. (Р// = 60,2 //tg Z) P= Ро+ ΔPB+ ΔPi.
Выгоднейшие условия наблюдений. При анализе формулы, сосинуса азимута светила
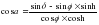
наиболее благоприятным временем для наблюдений Солнца является момент прохождения им плоскости первого вертикала. Однако чтобы обеспечить точность определения азимута в пределах 30" – 60// нет необходимости строго соблюдать это условие. Для широт 40° - 60° наблюдать Солнце рекомендуется в утренние (до 10 h) и вечерние (до 16 h) часы. Для ослабления влияния атмосферной рефракции высота Солнца должна быть при этом не менее 100 . Угловые измерения производятся теодолитами типа: Т30, Т2, Т5 и приборами, равными им по точности. Наблюдатель должен располагать ручными часами, радиоприемником, а также барометром - анероидом и термометром. Погрешности определения давления и температуры воздуха не должны превышать соответственно 5 мм. рт. ст. и 5°С. Погрешность определения среднего момента наблюдения Солнца по часам - не более 1м. 9. Вывод формулы из решения параллактического треугольника. Определяя азимут земного предмета по измеренной высоте светила, решают параллактический треугольник PZσ по трем сторонам и получают основную формулу для вычисления косинуса азимута светила на момент наблюдений.
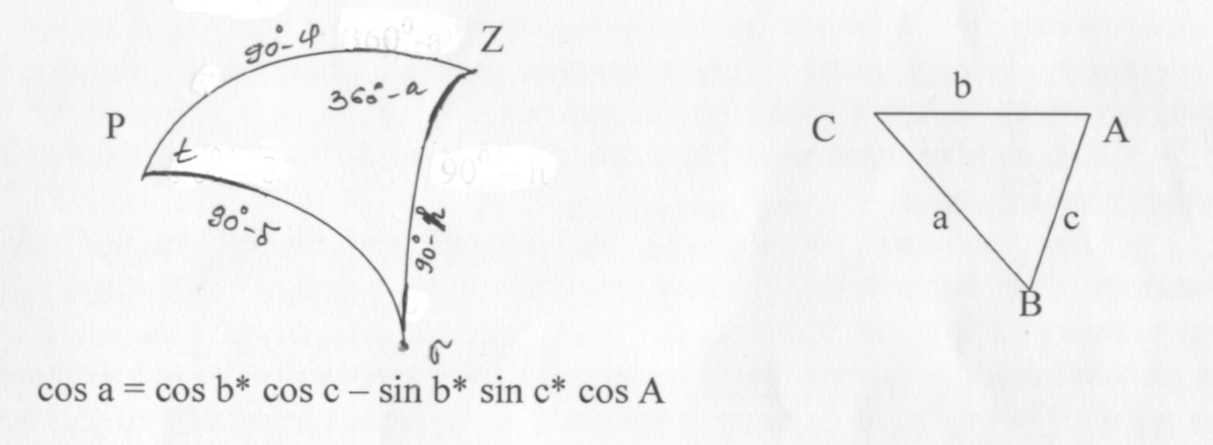
или из параллактического треугольника
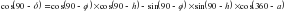
после преобразования получаем:
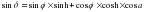
откуда получаем: 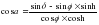
δ - склонение светила, выбираемое из астрономических таблиц по дате наблюдения и интерполируемое на момент наблюдений; φ - географическая широта точки наблюдения, определяемая по топографической карте возможно более крупного масштаба; h - высота светила, измеренная по вертикальному кругу теодолита, исправленная поправкой за астрономическую рефракцию. Высота светила является определяющим элементом данного способа. Вычислив по формуле азимут светила а и используя из журнала полевых наблюдений горизонтальный угол между направлениями на светило и местный предмет Q, находят азимут направления на местный предмет по формуле:
10. Полевая работа. Журнал наблюдений, контроль, допуски. В этом способе наблюдаемым светилом могут служить Солнце или яркие звезды. Если в качестве светила выбраны яркие звезды, результат определения азимута будет более точным, так как для наблюдений звезду можно выбирать вблизи первого вертикала и тем самым уменьшить до минимума влияние погрешности Δ h на точность азимута. В поле зрения трубы теодолита звезда имеет вид точки и наведение на нее центра сетки нитей осуществляется гораздо точнее, чем при визировании на диск Солнца значительных размеров (диаметр Солнца равен 31' в угловой мере). Для определения азимута с погрешностью 30"- 60" на практике чаще используется Солнце. Для удобства наблюдений на окуляр зрительной трубы теодолита надевают преломляющую призму, снабженную темным светофильтром для визирования на Солнце. Зрительную трубу заранее фокусируют на бесконечность и в дальнейшем эту фокусировку не меняют. Регулировку сетки нитей выполняют при наведении трубы на Солнце, добиваясь ее резкого и отчетливого изображения на фоне солнечного диска. Для данного способа определения азимута особенностью наблюдения на Солнце состоит в том, что и вертикальный h (Z) и горизонтальный Q должны быть измерены в один и тот же момент положения Солнца, которое непрерывно движется по небосводу. Для этого наведение на Солнце горизонтальной и вертикальной нитей сетки нужно выполнять одновременно. С этой целью, изображение Солнца наблюдают при двух положениях круга, в диаметрально противоположных четвертях поля зрения трубы, наводя в разных полу - приемах горизонтальную и вертикальную нить сетки нитей на противоположные края солнечного диска. При такой симметричной схеме наблюдений средние из отсчетов по горизонтальному и вертикальному кругам, будут относиться к центру Солнца, и к среднему общему моменту времени данного приема. В период утренних наблюдений наведение на Солнце осуществляют вначале в верхней правой четверти поля зрения трубы, во время вечерних - в левой верхней. Такой порядок визирования связан с характером видимого движения Солнца в течении дня.
Порядок визирования на диск Солнца при определении азимута по высоте Солнца
![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() Утренние наблюдения Вечерние наблюдения Утренние наблюдения Вечерние наблюдения
 
 
1 полуприем 1 полуприем  
 
2 полуприем 2 полуприем
Журнал наблюдений на Солнце «по высоте Солнца» С п.тр. Лагерная на п.тр. Нечаево Теодолит: Т5 № 4530 Дата: 1 августа 1986г. Время: Московское (n = 2) Широта: 54042,6/ Температура: t = +200C Долгота: λ = 2h29m00s = 37 015.0/ Давление: В = 768 мм.рт.ст.
| Объект наблюдений | Отсчет по часам | Отсчеты | Вычисления | | по вертикальному кругу | по горизонтальному кругу | | 1 полуприем (КЛ) | М – 0009,2/ | | п.тр. Нечаево |
|
| (1) 00 09,5/ | С = 110031,2/ | |  ![]() Солнце Солнце
![]()
| (2) 18 h49 m | (3) 156 0 52,5/ | (4) 109 0 42,5 | Q = 249038,0/ | | 2 полуприем (КП) |
| | ![]() Солнце Солнце
 ![]()
| (5) 18 h54 m | (6) 23005,5/ | (7) 2910 19,8/ |
| | п.тр. Нечаево |
|
| (8) 1800 09,0/ | Z = 66050.8/ | |
|
|
|
| h/ = 23009.2/ | | Тср = 18 h 52 m |
|
| 2с=+0,5/ | P = - 2.2/ | | u = +1m |
|
|
| h = 230 07.0/ | | T = 18 h 53 m |
|
|
|
| М – Средний отсчет по горизонтальному кругу на земной предмет С – Средний отсчет по горизонтальному кругу на центр Солнца. Q = М – С – Горизонтальный угол между земным предметом и Солнцем. 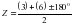 - Зенитное расстояние на центр Солнца. - Зенитное расстояние на центр Солнца. h/ = 900 – Z – Высота Светила (Солнца) Р – Поправка за влияние астрономической рефракции. (выбираем из астрономических ежегодников по аргументу Z). h – Высота Солнца с учетом поправки за астрономическую рефракцию. Тср – Среднее время наблюдений u – Поправка хода часов. Т – Среднее время наблюдений, с учетом поправки за ход часов. Контролем качества наблюдений в приеме служит двойная коллимационная погрешность на земной предмет (2с). Допустимая погрешность зависит прибора, и погрешности взятия отсчетов (2с  ±2m). ±2m).
Порядок визирования на диск Солнца при определении азимута по высоте Солнца полуприем при круге лево (КЛ). Наводят зрительную трубу на местный предмет и производят установку лимба, соответствующую данному приему. Затем более точно визируют на местный предмет и берут отсчет по горизонтальному кругу. Устанавливают на окуляре призму и светофильтр и направляют трубу на Солнце так, чтобы его изображение оказалось соответствующей четверти сетки; в момент одновременного касания краев солнечного диска горизонтальной и вертикальной нитей сетки берут отсчеты по часам, горизонтальному и вертикальному кругам. При работе с теодолитом без компенсатора перед отсчетом по вертикальному кругу приводят пузырек его уровня в нуль- пункт. полуприем при круге право (КП.) Переводят трубу через зенит и визируют трубу на Солнце, располагая его изображение в диаметрально противоположной четверти поля зрения трубы; берут отсчеты по часам, по горизонтальному и вертикальному кругу. Заканчивают прием повторным визированием на местный предмет; берут отсчеты только по горизонтальному кругу. Этот цикл наблюдений составляет один прием. Для определения азимута с точностью порядка 30-60// достаточно выполнить два таких приема. Однако во избежание не точного наведения на Солнце, а также в целях контроля и повышения точности результата, число приемов увеличивают до 4-6 на каждом пункте. При переходе к следующему приему меняют установку лимба, на угол равный 180°/n (n-число приемов). Полевым контролем служит постоянство двойной коллимационной погрешности (2с) на земной предмет. Обработка результатов полевых измерений Порядок вычислений, оценка точности. Вычисляют среднее из отсчетов по горизонтальному кругу при визировании на местный предмет 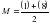 и среднее из отсчетов по горизонтальному кругу при визировании на Солнце. 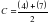 Вычисляют горизонтальный угол Q, между направление на местный предмет и на Солнце. Q = М - С Из отсчетов по вертикальному кругу на Солнце определяют измеренную высоту h Солнца, а затем его зенитное расстояние Z. Формула для вычисления h и Z зависит от типа применяемого теодолита. Для данного примера она имеет вид: 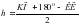 соответствующее зенитное расстояние будет равно: Z = 90° - h' По найденному зенитному расстоянию из «Таблицы поправок за среднюю рефракцию» выбирают среднюю поправку р0 за астрономическую рефракцию. С учетом давления В и температуры t в таблице находят поправки ΔРв и Δpt. Таким образом, суммарная поправка за рефракцию будет равна: р = ро + ΔРв + ΔРt исправленное значение высоты Солнца составит: h = h/ - P Определяют поправку часов и на средний момент Тср наблюдения Солнца в приеме. Из сравнения показаний часов с радиосигналами находят поправки ui и u2, с помощью которых вычисляют ход часов: 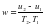 а затем и поправки: u = u1 + w (T – T1) = u2 +w(T – T2) Округлив значение u до 1m, находят исправленный момент D наблюдений по декретному времени: D = Т +u Определение склонения Солнца на момент наблюдения. В «Астрономическом календаре» в разделе «Солнце» приведены значения склонения Солнца на каждые сутки в 0h по всемирному времени (δ0), и v - часовые изменения склонения для интерполирования. δ = δ0 + vMh M h - всемирное время момента наблюдения выраженное в часах и долях часа. М = DM - (n+l)h, если время московское М = DM – Зh. Пример: Дата 17 мая; Время наблюдения DM= 8h37m. Часовой пояс п= 5; п+1=6 . M = 8h37m – 6h = 2h37m. Из «Астрономического календаря» по дате наблюдения δ0 =190 11/ 06//; v=+34,3// δ = 140°14'53". 9.3. Определение азимута по часовому углу Солнца 12. Вывод формулы для вычисления азимута Солнца. Выгоднейшие условия наблюдений. Поправка часов и ее интерполяция на момент наблюдений. Полевая работа. Журнал наблюдений, контроль, допуски. Сущность способа состоит в непосредственном измерении горизонтального угла между центром Солнца и земным предметом с фиксацией момента наблюдения по часам. Рассмотрим параллактический треугольник: 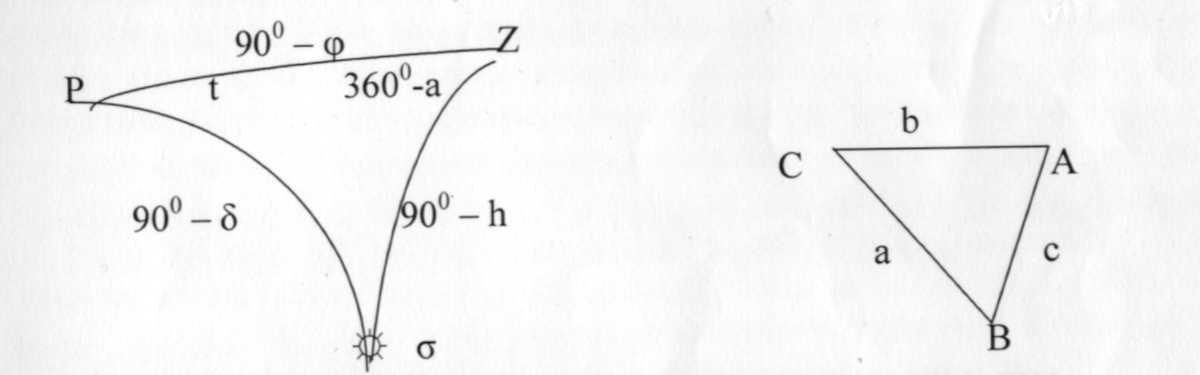
Параллактический треугольник решают в этом случае по двум сторонам Рσ = 90°-δ Pz = 90°-φ t - часовой угол Согласно теореме синусов: 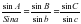 Можем записать для параллактического треугольника 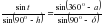
выполнив преобразования, получим:
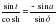
откуда получим: 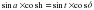
разделив на формулу пяти элементов 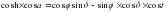 получим: φ- широта места наблюдения; δ - склонение Солнца на день наблюдений определяют по «Астрономическому календарю»; t - часовой угол Солнца определяют из полевых наблюдений; Q = M – C - горизонтальный угол между земным предметом и Солнцем; A = a – Q - азимут земного предмета. В отличии от способа определения азимута по измеренной высоте Солнца, где отсчет по часам необходим лишь для интерполяции склонения Солнца на момент наблюдений и притом с невысокой точностью (1m), в формуле азимута светила 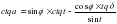
Часовой угол t является главным элементом определяющим, в конечном счете, точность полученного результата. Поэтому в этом случае время момента наблюдений и поправка часов должны быть известны с погрешностью не более 10s. Другая особенность способа определения азимута состоит в том, что в нем не измеряют вертикальные углы на светило. Поэтому на измерения не будет оказывать влияние астрономическая рефракция, в результате чего повысится точность окончательного результата. При этом значительно упрощается процесс визирования на Солнце, поскольку для измерения горизонтального угла важно фиксировать момент касания изображения солнечного диска лишь вертикальной нитью, горизонтальную нить достаточно навести приближенно на центр Солнца. Поэтому соответственно сокращается продолжительность наблюдения отдельного приема. Повышение точности определения азимута по часовому углу светила может быть обеспеченно лишь при наличии хронометра или качественных часов и достаточно точным определением поправки к ним. Организация полевых работ и методика наблюдений, мало чем, отличаются от способа определения азимута по измеренной высоте Солнца. Нет необходимости в термометре и барометре, так как нет необходимости введения поправки за астрономическую рефракцию, используются те же приборы, остается прежним количество приемов (4 -6) и допустимые погрешности угловых измерений. Поверку часов производят по радиосигналам более тщательно, с возможно большим интервалом, до и после наблюдений.
Журнал наблюдений. определения азимута «часовому углу Солнца»
С п.тр. Лагерная на п.тр. Рязаново Теодолит: Т5 № 4530 Дата:2 августа Широта: φ =54 °42,7' Долгота: λ =2 h 29.0' Сравнения показаний часов с радиосигналами: 6h - T1 = 6 h01 m30s u = -1 m 30s 10h - T2 = 10 h01m 02s u = +l m02 s
| ■ | | Объект наблюдения | Отсчет по часам |
| Отсчет по горизонтальному кругу | Вычисления | | 1 полуприем (КЛ) | | п.тр. |
|
| (1) 0°25,4; | М = 0025,4/ | |
|
|
| С = 288°07,0' | |  ![]() Солнце Солнце
![]()
| (2) 8 h36 m45s | (3) 287и39,5' | Q = 72° 18,4' | |
|
|
|
| | ![]() 2 полуприем(КП) 2 полуприем(КП)
| | ![]()  Солнце Солнце
| (4) 8 h36 m05s |
| (5) 108 034,4' |
| |
|
|
|
| | п. тр. |
| (6) 180°25,3' |
| |
|
| 2с = +0,1' |
| |
|
|
|
| | Tср | 8h37m25s |
|
| | u | - 1 m12 s |
|
| | D | 8h36m13s |
|
|
13. Вычисление часового угла Солнца. Часы отсчитывают время движения воображаемого «среднего Солнца», а фактически на небосклоне мы наблюдаем «истинное Солнце», которое в своем движении то обгоняет, то отстает от среднего Солнца на величину η (уравнение времени). Уравнение времени выражается формулой:
η = t0 - tm где откуда часовой угол истинного Солнца может быть выражен: to = η + t m Так как часовой угол среднего Солнца отсчитывается от момента верхней кульминации, то в гринвичскую полночь он будет равен 12h, т.е. tm = m + 12 h. Поэтому часовой угол t0 истинного Солнца на 0h всемирного времени определиться из соотношения: t0 = η + (m+12 h) Где среднее время на момент наблюдения для любой точки может быть выражено формулой: m = М + λ Подставим в формулу истинного Солнца и получим: t0 = η + М + λ +12 h или выполнив преобразования, получим: t0 = (η + 12 h) +М + λ Уравнение времени (η + 12 h) – определяется по «Астрономическому календарю» или «Каталогу координат Солнца и ярких звезд» на момент истинной полночи и должно быть исправлено за время прошедшее с момента истинной полночи поправкой за часовой изменение уравнения времени:
η + 12 h = (η0 + 12 h) + v*M h
подставив в формулу часового угла, получим:
to = (η0 + 12 h) + v*M h + М + λ
если выразить истинное время через декретное время получим:
t0 = (η0 + 12 h) + v*(Dm – 3 h) + Dm - 3 h + λ
Чтобы найти величину часового угла истинного Солнца, которое наблюдалось в кокой - то момент декретного времени данного часового пояса на пунктах с долготой (λ) необходимо: М = Tср – (n +1); выписать из «Ежегодника» по аргументу «Дата наблюдения» уравнение времени и часовое изменение уравнения времени (η0 + 12 h) и v; вычислить, часовой угол истинного Солнца (t0) в определенный момент всемирного времени, для точки земной поверхности, имеющей определенную долготу ( λ ). Точность способа зависит от точности измерения времени наблюдения.
9.4. Определение азимута по часовому углу Полярной.
Вывод упрощенной формулы. Составление эфемерид Полярной. Полевые наблюдения и их организация. Журнал измерений, контроль, допуски, вычисление, оценка точности. 16. Вывод упрощенной формулы. В геодезии из всех звезд, используемых для приближенных способов определения азимута, наиболее удобной в практическом отношении является Полярная звезда. Полярную звезду легче отыскать на небосводе по ее расположению в созвездии Малой Медведицы, чем любую другую звезду.
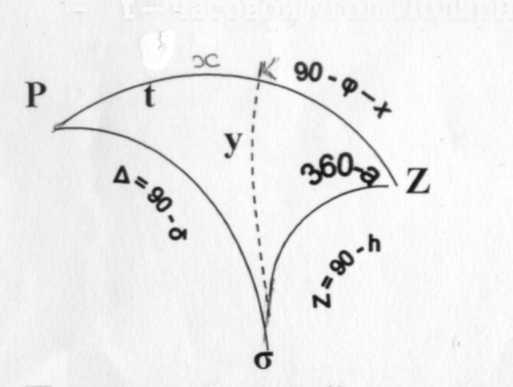
Параллактический треугольник PZσ, одной из вершин которого является Полярная звезда, имеет особую форму. По сравнению с остальными сторона Рσ = 90° - δ весьма мала, соответственно этому мал и угол а или (360° - а) при вершине Z, т.е. азимут светила. При приближенном определении азимута это позволяет решать треугольник более просто, чем в общем случае и, следовательно, облегчить и сократить объем вычислений. Как и в предыдущем способе, параллактический треугольник решают по сторонам: PZ = (90° - φ) - зенитное расстояние; Рσ = (90° - δ) - полярное расстояние; t - часовой угол Полярной звезды
Построим большой круг перпендикулярно меридиану в точке К, получим два сферических прямоугольных треугольника: Δ РКσ Δ KZσ Рассмотрим треугольник Δ РКσ по теореме синусов можем записать отношение:
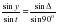
Однако sin 900= 1 Поэтому, выполнив преобразование, получим:
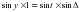
В следствии малости величины дуг: Δ= (90° - δ) и у заменим их радианной мерой:
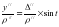
откуда после преобразования получим: Из треугольника РКσ полагая, что угол при светиле σ = 90° - t, так как треугольник прямоугольный, значит один из углов равен 90°, второй угол часовой угол светила t, то третий угол в треугольнике может быть найден по формуле: (90° - t), то по тереме синусов можем для данного треугольника записать: 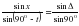
или выполнив преобразования, получим: 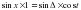 или
Рассмотрим треугольник KZσ. Теорема тангенсов: 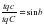
Из треугольника Δ KZσ по теореме тангенсов получим:
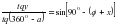
или выполнив преобразования, получим: 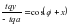
Откуда получим: 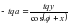
или заменив значения тригонометрических функций значениями их углов, получим:
заменив значения у, х их значениями получим:
Из формулы получают непосредственно азимут Полярной звезды, который вследствие малости значения азимута будет иметь значения угла в секундах.
Δ // = 90 0 – δ – полярное расстояние светила может быть вычислено по склонению светила, которое определяется из «Астрономического ежегодника» по аргументу «Дата наблюдения». φ – широта места наблюдения, определяется по топографической карте. t – часовой угол светила, определяется при полевых измерениях. α – прямое восхождение светила, определяется из «Астрономического ежегодника», по аргументу «Дата наблюдения». S = α + t – звездное время, откуда может быть вычислен часовой угол t = S + α
17. Составление эфемерид Полярной.
Эфемериды Полярной звезды - это приближенные горизонтальные координаты Полярной звезды. Азимут по часовому углу Полярной звезды можно определять не только ночью, но и днем. Полярная звезда будет видна на голубом небе как светящаяся голубая точка в зрительную трубу с увеличением в 30 крат и более. При подготовке к наблюдениям выполняют расчет эфемерид Полярной. Приближенные горизонтальные координаты: Зенитное расстояние для светила может быть вычислено по формуле: Z = 90°- h а для Полярной звезды : 90° - h = 90° - φ - х откуда можно вычислить: h = ф + х; обозначим х = f тогда получим: h = ф + f
f - функция времени f = х Δ// cos t
где t = S - α
тогда получим:
Вычисление рабочих эфемерид Полярной
φ = 54°43; Дата наблюдений: 10 мая 1970 г. λ = 37°25/ = 2 h29,7m Время московское. (п=2)
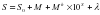
h = ф + f
| № п/п | Обозначение | Предполагаемые моменты наблюдений | Примечание | | 1 | Dm | 22h00m | 22h30m |
| | 2 | -Зh | Зh | 3h |
| | 3 | M = Dm-(n+l) | 19h00m | 19h30m |
| | 4 | Mh*10s | 190s=3,2m | 195s=3,3m |
| | 5 | So | 19h10,0m | 19h10,0m | Ежегодник «Дата наблюдений» | | 6 | λ | 2 h29,7m | 2 h29,7m |
| | 7 | S | 16h42,9m | 17h12,9m |
| | 8 | f | - 0°39; | - 0°34/ | Ежегодник «Видимые места Полярной» | | 9 | φ | 54°43/ | 54°43/ |
| | 10 | h | 54004/ | 54009/ |
| | 11 | а | +0°58/ | +10 06/ | Ежегодник «Видимые места Полярной» |
18. Полевые наблюдения и их организация. Журнал измерений, контроль, допуски. Главный элемент формулы t - часовой угол Полярной, - вычисляют как функцию местного звездного времени S и прямого восхождения α светила. t = S – α Величины α и δ (экваториальные координаты светила) приводятся в «Астрономическом ежегоднике» в специальных таблицах «Видимые места Полярной» Каталога координат Солнца и ярких звезд». Изменения экваториальных координат весьма малы, поэтому при их выборе на дату наблюдений интерполяция на момент наблюдений не требуется. Как объект наблюдений, Полярная звезда имеет ряд преимуществ по сравнению с Солнцем. Визирование на нее производится значительно легче и точнее, так как ее изображение представляется в виде мало подвижной точки, в отличие от крупного и быстро перемещающегося Солнечного диска. Кроме того, наблюдения Полярной звезды можно осуществлять не только ночью, но и в светлое время суток. Для этого необходимо заранее составить специальную таблицу приближенных горизонтальных координат (рабочие координаты – эфемериды) - азимута (а) Полярной звезды - высоты (h) Полярной звезды.
Эфемериды Полярной звезды - это приближенные горизонтальные координаты Полярной звезды. Выполнив ориентирование прибора по их значениям, можно найти изображение звезды в поле зрения трубы. Определение азимута по часовому углу Полярной звезды может быть выполнено с более высокой точностью, чем по Солнцу. При той же методике наблюдений погрешность результатов не превысит 10-15 ", если использовать теодолит типа Т2 или равный ему по точности и увеличить число наведений на светило и земной предмет в два раза. Вычисления в этом случае следует выполнять по основной формуле.
Этот способ определения азимута по Полярной звезде применяется, например, при передаче дирекционных углов с пункта триангуляции и полигонометрии на ориентирные пункты. Особенностью расположения Полярной звезды на небесной сфере по сравнению с Солнцем является ее значительная высота над горизонтом. В средних широтах она достигает величины 40° и более. Поэтому на окуляр зрительной трубы и отсчетного микроскопа обязательно надевается преломляющая насадка. В дневное время невооруженным глазом Полярная звезда не видна, но в поле зрения трубы теодолита она имеет вид серебристой точки. Несмотря на четкое изображение Полярной звезды во время ночных наблюдений, нельзя быть полностью уверенным, что наблюдается именно Полярная звезда, а не другая, расположенная рядом звезда. Поэтому независимо от времени суток, наблюдатель должен располагать рабочими эфемеридами Полярной звезды. При отыскании Полярной звезды на небосклоне зрительную трубу теодолита необходимо фокусировать на бесконечность. Журнал наблюдений определения азимута по часовому углу Полярной
С п.тр. Лагерная на п.тр. Осинки. Теодолит Т5 №4530 Дата: 5 августа 1986 г. Время: Московское n=2 Широта: φср = 54°42/42// Долгота: δ == 37°15/00// Сравнение показаний часов с радиосигналами: 22h – T1 = 21h59m30s u1=+00m30s 2h - T2 = 1h 58m57S | Объект | Время наблюдений | Отсчет no горизонтально му кругу |
| Вычисления | | 1 полуприем (КЛ) | М=0007,б/ | | п.тр. Осинки |
| (1)0°07,б/ |
| С=197°58,0/ | | Полярная
| 22h45m25S | 197°56,6/ |
| Q= 162°09,6/ | | 2 полуприем (КП) |
| | Полярная
| 22h50m00S | 17059,7/ |
|
| | п.тр. Осинки |
| 180007,7/ | 2с=-0,1/ |
| |
| Tcp=22h47m42S |
|
|
| |
| u = +36S |
|
|
| |
| D = 22h48m18S |
|
|
|
Вычисление поправки часов: 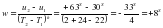 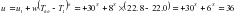 | 








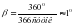
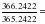 звездных суток =
звездных суток = 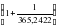 звездных суток
звездных суток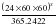 = 1 звездным суткам + 3m 57S
= 1 звездным суткам + 3m 57S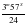 ;
;


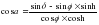

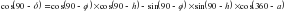
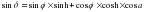



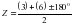 - Зенитное расстояние на центр Солнца.
- Зенитное расстояние на центр Солнца. ±2m).
±2m).