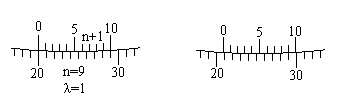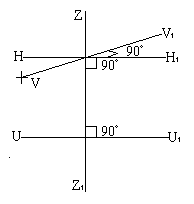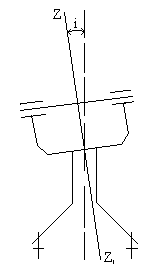| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН КОЛЛЕДЖ ГЕОДЕЗИИ И КАРТОГРАФИИ 
ОТКРЫТЫЙ УРОК
Раздел: 3. Угловые и линейные измерения. 3.2 Устройство и поверки теодолитов. Тема: Назначение, устройство, основные части технических теодолитов Т30, 2Т30, установка прибора в рабочее положение.

Преподаватель Федорук Е.К. г. Семей
2015-2016 г.
План урока
ГРУППА: 203 ДАТА: 29.11.15 ТЕМА: Раздел 3. Угловые и линейные измерения. 3.2. Устройство и поверки теодолитов ТИП УРОКА: Урок формирования умений и навыков Лабораторная работа № 9 ЦЕЛИ УРОКА ОБРАЗОВАТЕЛЬНАЯ: Познакомить учащихся c устройством теодолитов Т5, Т5К, Т30. Установка прибора в рабочее положение. Отсчитывание по кругам. ВОСПИТАТЕЛЬНАЯ: Воспитание интереса к предмету, выбранной профессии. Позитивного отношения к учебе, жизни, отношению в коллективе. РАЗВИВАЮЩАЯ: Развитие представления о назначении, видах, устройстве теодолитов Т30,Т15 Установка прибора в рабочее положение. Отсчитывание по кругам. Правила обращения с приборами. МЕЖПРЕДМЕТНЫЕ СВЯЗИ: ОБЕСПЕЧЕНИЕ ЗАНЯТИЯ УЧЕБНО-НАГЛЯДНЫЕ ПОСОБИЯ ВЕРБАЛЬНЫЕ СРЕДСТВАОБУЧЕНИЯ: «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г. Плакат СПЕЦИАЛЬНОЕ ОБОРУДОВАНИЕ Теодолит Т30 – 1 на 2 учащихся Буссоль Мультимедийная установка.
ПЛАН УРОКА
| № | НАИМЕНОВАНИЕ СТРУКТУРНОГО ЭЛЕМЕНТА УРОКА | ВРЕМЯ | | 1 | Организация урока: Получение приборов, литературы, установка приборов. Приветствие Проверка присутствующих | 5 | | 2 | Постановка цели и задания на урок Тема: 3.2. Устройство и поверки теодолитов Цель: Изучить основные части теодолита устройство, назначение, оси, виды. Устройство теодолитов Т30, Т15. Установка прибора в рабочее положение. Научиться наводить на предмет, производить отсчеты по горизонтальному и вертикальным кругам теодолита.. Задание: Изучить устройство, назначение , виды, основные оси зрительных труб геодезических инструментов. Сетка нитей. «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г § 29 стр. 75 рис. 42 стр. 76 рис. 43,44 Изучить виды, назначение, оси, устройство уровней. «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г § 28 стр. 74 рис. 41 Изучить виды, назначение отсчетных устройств теодолитов «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г § 30 стр. 78 рис. 45,46 Изучить назначение, основные части, оси, устройство теодолитов (Т30, Т15). «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г § 31 стр. 80 рис. 48,50 Изучить и выполнить установку прибора в рабочее положение «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра»1985г § 33 Получить зачет. Оформить работу. | 5-10 | | 3 | Объяснение Устройство, назначение, виды, основные оси зрительных труб геодезических инструментов. Установка зрительной трубы для наблюдений. Сетка нитей, назначение, виды, оси, устройство. Назначение, виды, оси, устройство уровней. Виды, назначение отсчетных устройств теодолитов. Назначение, основные части, оси, устройство теодолитов (Т30, 2Т30). Установка прибора в рабочее положение. | 20-25 | | 4 | Выполнение задания Самостоятельная работа с литературой. Самостоятельная работа с прибором. Работа с литературой, прибором в команде. Предложить учащимся составить бригаду (команда) для работы с прибором. – 2 студента. Поставить цель, задание на урок. Предложить работать в команде, изучая устройство прибора, прорабатывая отдельные вопросы устройства, задачи наведения, отсчитывания. Зачет по теме. Каждая команда сдает и получает зачет по теме индивидуально, бригадой, при этом члены команды могут помогать членам своей команды. Взаимообучение, работа в команде по каждому вопросу, на каждом этапе, позволяет всем студентам следить за работой каждой команды, каждого студента. Если учащиеся получают отметку, которая их не устраивает, они могут повысить свой балл, повторив ответ, подготовившись дополнительно, или выполнив отдельный этап наведения, отсчитывания. | 40-45 | | 5 | Задание на дом Выполнить оформление работы. «Ассур В.Л., Филатов А.М. «Практикум по геодезии». Москва «Недра» 1985г § 29 стр. 75 рис. 42, стр. 76 рис. 43,44; § 28 стр. 74 рис. 41 § 30 стр. 78 рис. 45,46 § 31 стр. 80 рис. 48,50; § 33 | 2-5 | | 6 | Литературу, проверить и сдать в библиотеку. Приборы проверить, собрать и сдать в лаборантскую геодезии. | 2-5 |
Самоанализ Открытого урока Группа: 203 Предмет: Геодезия Дата: 29.11.15 ТЕМА: Раздел 3. Угловые и линейные измерения. 3.2. Устройство и поверки теодолитов ТИП УРОКА: Урок формирования умений и навыков Лабораторная работа № 9 ЦЕЛИ УРОКА ОБРАЗОВАТЕЛЬНАЯ: Познакомить учащихся c устройством теодолитов Т5, Т5К, Т30. Установка прибора в рабочее положение. Отсчитывание по кругам. ВОСПИТАТЕЛЬНАЯ: Воспитание интереса к предмету, выбранной профессии. Позитивного отношения к учебе, жизни, отношению в коллективе. РАЗВИВАЮЩАЯ: Развитие представления о назначении, видах, устройстве теодолитов Т30,Т15 Установка прибора в рабочее положение. Отсчитывание по кругам. Правила обращения с приборами. 1.Урок цели достиг. ТДЦ поставленные на урок успешно реализованы. Учащиеся группы успешно изучили устройство, назначение, виды, основные оси зрительных труб геодезических инструментов. Учащиеся группы успешно изучили сетку нитей, назначение, виды, оси, устройство. Учащиеся группы успешно изучили назначение, виды, оси, устройство уровней. Учащиеся группы успешно изучили виды, назначение отсчетных устройств теодолитов. Учащиеся группы успешно изучили назначение, основные части, оси, устройство теодолитов (Т30, 2Т30). Учащиеся группы успешно выполнили установку зрительной трубы для наблюдений. Научились выполнять отсчеты по горизонтальному и вертикальному кругу. Учащиеся группы успешно сдали зачет, получили положительные оценки за урок. Учащиеся группы успешно оформили материалы лабораторной работы, и сдали материалы в срок. 2. При планировании урока учла особенности и возможности учащихся, их знание, умение построить ответ, умение говорить, умение работать, работать в команде. Данный урок первый при изучении темы «Угловые и линейные измерения». Данный урок - Урок знакомства с геодезическими приборами, оборудованием, с которыми студентам в их будущей профессии придется работать постоянно. Важно создать позитивное, заинтересованное отношение к геодезическим приборам. За годы обучения в колледже студенты должны хорошо изучить, научиться уверенно работать с приборами. Геодезия – это наукоемкая, постоянно изменяющиеся, в тоже время, имеющая традиционные методики, способы работы, приборы. Важно научить студентов учиться, а непросто изучить какие-то вопросы, приборы, усвоить какой-то материал. Следует отметить, что недостаточно сформировать группы и дать им соответствующее задания. Суть как раз и состоит в том, чтобы учащийся захотел сам приобретать знания. Восточная мудрость гласит: Можно коня привести к воде, Но нельзя заставить его пить. Поэтому, если удается заставить ребят испить хоть однажды из вечного источника знаний и получить от этого удовольствие, преодолеть робость, стереотипы, можно быть уверенными, что они не забудут вкус победы, и постарается его повторить в будущем. Поэтому проблема мотивации самостоятельной учебной деятельности учащихся не менее, может быть более важна, чем способ организации, условия и методика работы над заданием. «Личностно ориентированное обучение - это такое обучение, где во главу угла ставится личность обучающегося, ее самобытность, самоценность; субъектный опыт каждого сначала раскрывается, а затем согласовывается с содержанием обучения». 3. Урок лабораторный, урок формирования умений и навыков, оснащение приборами на уроке достаточное, позволило всем учащимся индивидуально поработать с приборами, что очень важно, т.к. выпускники колледжа практики, и должны уверенно работать с геодезическими приборами. 3. Атмосфера на уроке спокойная, рабочая, доброжелательная. Чувствовалось, что учащиеся переживали, хорошо подготовились, к уроку. Дисциплина на уроке хорошая. 4. Все поставленные задачи на уроке реализованы. Урок прошел на хорошем уровне. 4. Время на уроке было распределено рационально, все этапы урока выполнены, связи между этапами урока закономерны и логичны. Преподаватель Федорук Е.К. 2015 – 2016 учебный год. ПРОТОКОЛ № от 08.12.15 Заседания цикловой комиссии «Аэрофотогеодезии» Присутствовуют: Романова И. П. Шевченко О. А. Дронова О.М. Бексултанова З.Б. Баркова Е.Л. Повестка: Обсуждение открытого урока по предмету «Геодезия» по теме «Угловые и линейные измерения. Устройство и поверки теодолитов» в группе 203 преподаватель Федорук Е.К. Ход заседания: Самоанализ урока провел преподаватель Федорук Е.К. Лабораторная работа № 9. Урок формирования умений и навыков. Цель урока: Познакомить учащихся c устройством теодолитов Т5, Т5К, Т30. Научить учащихся выполнять установку прибора в рабочее положение. Научить отсчитывать по кругам. Воспитание интереса к предмету, выбранной профессии. Позитивного отношения к учебе, жизни, отношению в коллективе. Развитие представления о назначении, видах, устройстве теодолитов Т30,Т15 Установка прибора в рабочее положение. Отсчитывание по кругам. Правила обращения с приборами. Урок цели достиг. ТДЦ поставленные на урок успешно реализованы. Учащиеся группы успешно изучили устройство, назначение, виды, основные оси зрительных труб геодезических инструментов. Учащиеся группы успешно изучили сетку нитей, назначение, виды, оси, устройство. Учащиеся группы успешно изучили назначение, виды, оси, устройство уровней. Учащиеся группы успешно изучили виды, назначение отсчетных устройств теодолитов. Учащиеся группы успешно изучили назначение, основные части, оси, устройство теодолитов (Т30, 2Т30). Учащиеся группы успешно выполнили установку зрительной трубы для наблюдений. Научились выполнять отсчеты по горизонтальному и вертикальному кругу. Учащиеся группы успешно сдали зачет, получили положительные оценки за урок. Учащиеся группы успешно оформили материалы лабораторной работы, и сдали материалы в срок. При планировании урока учла особенности и возможности учащихся, их знание, умение построить ответ, умение говорить, умение работать, работать в команде. Данный урок первый при изучении темы «Угловые и линейные измерения». Данный урок - Урок знакомства с геодезическими приборами, оборудованием, с которыми студентам в их будущей профессии придется работать постоянно. Важно создать позитивное, заинтересованное отношение к геодезическим приборам. За годы обучения в колледже студенты должны хорошо изучить, научиться уверенно работать с приборами. Геодезия – это наукоемкая, постоянно изменяющиеся, в тоже время, имеющая традиционные методики, способы работы, приборы. Важно научить студентов учиться, а непросто изучить какие-то вопросы, приборы, усвоить какой-то материал. Следует отметить, что недостаточно сформировать группы и дать им соответствующее задания. Суть как раз и состоит в том, чтобы учащийся захотел сам приобретать знания. Поэтому, если удается заставить ребят испить хоть однажды из вечного источника знаний и получить от этого удовольствие, преодолеть робость, стереотипы, можно быть уверенными, что они не забудут вкус победы, и постарается его повторить в будущем. Поэтому проблема мотивации самостоятельной учебной деятельности учащихся не менее, может быть более важна, чем способ организации, условия и методика работы над заданием. «Личностно ориентированное обучение - это такое обучение, где во главу угла ставится личность обучающегося, ее самобытность, самоценность; субъектный опыт каждого сначала раскрывается, а затем согласовывается с содержанием обучения». Урок лабораторный, урок формирования умений и навыков, оснащение приборами на уроке достаточное, позволило всем учащимся индивидуально поработать с приборами, что очень важно, т.к. выпускники колледжа практики, и должны уверенно работать с геодезическими приборами. Атмосфера на уроке спокойная, рабочая, доброжелательная. Чувствовалось, что учащиеся переживали, хорошо подготовились, к уроку. Дисциплина на уроке хорошая. Все поставленные задачи на уроке реализованы. Урок прошел на хорошем уровне. Время на уроке было распределено рационально, все этапы урока выполнены, связи между этапами урока закономерны и логичны.
Баркова Е.Л.: зав. отделением: Урок цели достиг. Хороший современный урок, с использованием инновационных педагогических технологий. Урок имеет большое мотивационное значение для студентов в стремлении осваивать геодезические приборы. Урок лабораторный, все задачи поставленные на урок выполнены. Работа учащихся на уроке оценена. Преподаватель владеет материалом, умело направляет и организует работу студентов на уроке. Романова И. П. преподаватель спец.дисциплин. Урок цели достиг. Учащиеся изучили устройство теодолита, на протяжении всего урока учащиеся проявляли заинтересованность, интерес к уроку, предмету. На уроке демонстрировались наглядные пособия, приборы, что способствовало успешному выполнению задания. Обстановка на уроке рабочая, доброжелательная. Шевченко О. А. председатель цикловой комиссии: Урок проведен замечательно. Учащиеся с удовольствием находились на уроке, выполняли задание поставленное на урок. Урок цели достиг. Доброжелательная обстановка на уроке. Дронова О.М. преподаватель спец.дисциплин. Урок цели достиг, соответствует календарно-тематическому плану, прошел интересно, ребята активно работают на уроке, используется раздаточный материал, литература, приборы. Учащиеся получили навыки работы с геодезическими инструментами. Учащиеся проявляют профессиональный интерес к выбранной профессии. Бексултанова З.Б. преподаватель спец.дисциплин: Урок соответствует КТП, прошел интересно, ребята активно работают на уроке, используется раздаточный материал. Учащиеся получили навыки обращения с приборами. На уроке доброжелательная атмосфера, у ребят появляется профессиональный интерес к выбранной профессии. Решение: Открытый урок считать проведенным на современном уровне. Рекомендуем использовать данный опыт при проведении уроков. Председатель: Абдрашитова О.Л.__________________ ФОРМИРОВАНИЕ ПРОФЕССИОНАЛЬНЫХ УМЕНИЙ И НАВЫКОВ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ НАГЛЯДНО ДИДАКТИЧЕСКОГО МАТЕРИАЛА. Основными целями системы среднего профессионального образования являются подготовка специалистов среднего звена и создание условий для развития личности в образовательном процессе. Профессионал – это специалист, обладающий системой знаний, умений и навыков позволяющие ему выполнить производственное задание с хорошим качеством, это специалист умеющий отстоять свою точку зрения, пользующийся уважением в коллективе, и осваивающий новые технологии, возникающие в современном производстве. Условия на рынке труда сложились так, что наши выпускники востребованы на производстве, но это только повышает требование к качеству подготовки конкурентно способного компетентного специалиста. Прежде всего, нужно исходить из того, что должен знать и уметь специалист топографо–геодезического производства: знать и уметь работать на геодезических и фотограмметрических инструментах и приборах, знать технологию выполнения работ, знать и уметь работать со справочной и регламентирующей литературой, уметь выполнять контроль и анализ выполненной работы, уметь организовать работу. Особенностью предметов «Геодезия», «Высшая геодезия», «Фотограмметрия», «Электронные геодезические средства измерений» является интерес, обусловленный новизной информации. Ребята нового набора видят, как учащиеся старших курсов работают с инструментами и ждут, не дождутся когда же и они научатся работать на этих инструментах. Новизна информации присутствует при изучении всего курса геодезии, например на уроках геодезии, в течение первого месяца обучения учащиеся получают очень много абсолютно новой информации (около 30-40 новых понятий и определений). Но здесь возникает другой момент, - учащийся не должны потонуть под этой лавиной информации, он должен не только освоить эту информацию, но и уметь работать с ней. Объем информации такой, что нет возможности дать каждому учащемуся высказаться, проверить степень усвоения материала, программой не предусмотрены дополнительные часы на повторение и закрепление теоретического материала. Поэтому нужно тщательно организовать обучение, так построить урок и мотивировать работу учащихся, чтобы он самостоятельно стремился освоить материал, анализировал, учился работать, выполнять домашнее задание преподавателя, то есть учить рефлексии. То есть должен быть мощный мотив, побуждающий учащегося стремиться к обучению. Аспектов возникновения мотива обучения много, но я хочу остановить на некоторых. Во-первых - профессиональный интерес и в будущем успешная работа. Во-вторых - уважение и любовь к профессии и к преподавателю. Наша деятельность такова, что уважение это не пьедестал и не щит, с которым мы входим в кабинет, начиная урок. Мы ежеминутно утверждаем и подтверждаем свой статус «Учитель». Уважение не может быть односторонним, необходимо относиться к каждому учащемуся как к личности, уважать его. Только работая в сотрудничестве «педагог - ученик», уважая друг друга, работая вместе, в одной команде, будучи единомышленниками можно добиться успеха. Развивать профессиональный интерес, профессиональную гордость, профессиональную ответственность за свой труд можно по-разному, и всегда можно и нужно найти место и время обозначить и подчеркнуть этот момент. Например: - При изучении условных знаков топографических карт, и говоря о достоверности карты приводим пример, что, изображая колодец или озеро топограф проявив небрежность или по невнимательности не подписал 3 маленькие буквы – сол. – и, может случиться беда. - Подписываем название вершины горы или аула – небрежность, безответственность топографа выполнявшего сбор информации и нет доверия к карте. - Выполняет геодезист трассирование автомобильной дороги – небольшая неточность в работе – и брак в работе геодезиста выливается в кубометры и тонны асфальта или аварии на дороге. Народная пословица говорит: То – что написано пером, не вырубишь топором. И эту истину ребята постигают на собственном опыте. В работе педагога нет мелочей. Урок это 90 минут. Это много и мало, всегда хочется так много успеть на уроке, обо все рассказать, всему научить. Для повышения качества подготовки специалистов существенное значение имеет уровень развития и применение наглядно-дидактического материала в процессе обучении. Наглядно-дидактический материал это совокупность предметов (инструменты, приборы, оборудование), учебно-наглядных пособий и средств обучения, которые позволяют увеличить самостоятельность работы учащегося, расширить возможности организации работы на уроке, организовать индивидуальную и групповую работу, развивать умственную активность и инициативу при усвоении рабочего материала. Изучение предмета геодезия предполагает изучение различных геодезических инструментов, и здесь для демонстрации используется, конечно, сам инструмент, и, кроме того, схематические рисунки, показывающие основные оси инструмента, которые я обычно рисую на доске, и обязательно применяются плакаты, показывающие детально внутреннее устройство и ход лучей. Техник – геодезист должен досконально знать устройство прибора, уметь выполнить поверки и при необходимости устранить неисправности. Особенно остро вопрос умения исправить самостоятельно инструмент стоит сейчас, когда разрушены в Казахстане инфраструктура т.г.пр-ва. Геодезист должен уметь произвести отсчет, уметь правильно его записать, выполнить обработку, и дать заключение о качестве наблюдений. Для того чтобы развивать эти навыки, на уроках широко применяем работу на специальных бланках журналов и ведомостей, и при объяснении использую плакаты, дублирующие бланковую продукцию, на которых можно продемонстрировать как, ведется запись, обработка, контроль, возможные ошибки и способы их исправления. Специалист топографо-геодезического производства должен знать требования регламентирующей и справочной литературы и уметь работать с ней. Поэтому на уроках постоянно использую справочную литературу: «Инструкция по топографической съемке в масштабах 1:5 000 – 1: 500» «Инструкция о построении государственной геодезической сети» «Инструкция по нивелированию I,II,III,I\/ классов» и др. Предлагаю поработать самостоятельно дома, но при этом обязательно указываю конкретные вопросы, на которые необходимо найти ответы, а не просто составить конспект или познакомиться с требованиями инструкции. Например: Найти ответы на вопросы: Какова допустимая длина луча визирования; Допустимая высота луча визирования над подстилающей поверхностью; Допустимая разность плеч, допустимое накопление; Указать величину допустимого расхождения в превышениях; и др. Китайская пословица гласит: Я – слышу – я забываю. Я – вижу – я запоминаю. Я – делаю – я понимаю. И это абсолютно верно. Только выполняя работу самостоятельно или под руководством преподавателя – выполняя измерение угла, заполняя журнал, выполняя его обработку, анализ, решая геодезические задачи - учащиеся могут освоить процесс, причем следует отметить, что необходимо многократное его выполнение. Поэтому на уроках постоянно использую различный наглядно дидактический материал на разных этапах урока, и разного содержания, назначения и объема: при изучении нового материала, при проверке усвоения материала, при закреплении, при повторении, при подготовке к государственным экзаменам. Самостоятельная работа помогает усвоить материал и активизировать процесс обучения, побуждая учащихся выполнять работу самостоятельно, контролировать результат, и проверить свои возможности. На уроках теоретического обучения при изучении нового вида работ или отдельных процессов применяю самостоятельную фронтальную работу. Применяю индивидуальные задания для самостоятельной работы на этапе контроля усвоения материала, при повторении или закреплении. При проведении лабораторных и практических работ практикую выполнение работ только по индивидуальным заданиям или работу в малых группах. Например: «Вычисление прямой геодезической задачи»; «Вычисление координат точек теодолитного хода» «Измерить горизонтальный угол способом отдельного приема». «Выполнить исследование метровых делений реек». Причем в этом случае имитируется производственная ситуация, когда специалист выполняет измерения или обработку результатов. Еще хочу отметить необходимость обязательной оценки работы учащегося. Труд, любой труд, а учеба это сложная работа должна быть замечена, одобрена, оценена. Для того чтобы быстро проверить работу, указать на ошибки, и оценить качество выполненной работы для индивидуальных заданий готовлю решения и ответы, это значительно экономит время на уроке, но требует большой предварительной работы. Научно-технический прогресс вносит свои изменения в технологию обработки результатов геодезических данных. И мы применяем различные программы обработки информации на ПЭВМ, не заменяя, а, дублируя или применяя для контроля работ, для того чтобы подготовить учащихся к работе на производстве, где более широко используются возможности программного обеспечения обработки результатов геодезических измерений. Особенностью подготовки специалистов топографо-геодезического производства состоит в том, что науки геодезия, фотограмметрия, – это наукоемкие дисциплины, и научно-технический прогресс и бурное развитие приборостроения, буквально выбросили на рынок лавину новейших геодезических, фотограмметрических приборов (тахеометров, светодальномеров, компьютерных программ), поэтому нужно подготовить учащихся осваивать новые технологии, приборы, научить учиться, преодолевать себя, и сложности в работе. «Преподаватель среднего специального учебного заведения своими знаниями, поведением, отношением к делу уже формирует определенное отношение к учебному предмету, к специальности и трудовой деятельности, к жизни. Влияние педагога настолько сильно, что для многих воспитанников он становится образцом, идеалом, а их личные устремления направлены на достижение того совершенства, которое они видят в своем учителе».
Конструктивные элементы геодезических измерительных приборов 3.1. Отсчетные приспособления Измерить какую-либо величину - значит сравнить ее с другой однородной величиной, принятой за единицу измерения. Приспособление, несущее единицу измерения, называется рабочей мерой. Обыкновенная линейка с делениями сантиметров и миллиметров, транспортир с делениями градусов - это примеры рабочих мер. Шкала рабочей меры как правило равномерна; она может располагаться по прямой линии, по дуге окружности или по какой-либо другой кривой. Отсчитывание по шкале рабочей меры производят по отсчетному индексу (начало и конец отрезка линии, сторона угла, штрих логарифмической линейки, стрелка весов и т.п.). В общем случае отсчетный индекс (на рис.3.1. - О.И.) устанавливается между двумя штрихами шкалы; один из них называют младшим штрихом (мл.), другой - старшим (ст.). 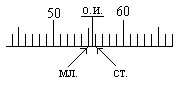 Рис.3.1 Отсчет N по шкале равен сумме двух величин: N = Nмл + x, (3.1) где Nмл - значение младшего штриха шкалы, Nмл = 55,
x - доля цены деления шкалы от младшего штриха до отсчетного индекса, x = 0,6. Величину x можно получать разными способами, простейший из них - оценивание на глаз. Другой способ предполагает наличие специального отсчетного приспособления, назначение которого - измерять величину x с той или иной точностью. Известны следующие отсчетные приспособления: в машиностроении - нониус (верньер), микрометр, микроскоп-микрометр, в оптическом приборостроении, штриховой и шкаловой микроскопы, оптический микрометр и т.д. Верньер - одно из простейших отсчетных приспособлений. Его строят следующим образом: отрезок в n делений шкалы рабочей меры (основной шкалы) переносят на прилегающую поверхность и делят его там на ( n + 1 ) равных частей, получая шкалу верньера (рис.3.2). Обозначим через λ цену деления основной шкалы и через μ - цену деления верньера; точностью верньера t называют разность t = λ - μ. (3.2) По построению λ * n = μ * ( n + 1 ), поэтому 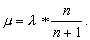 Подставив это выражение в формулу (3.2), получим 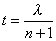 (3.3) (3.3) то-есть, точность верньера равна цене деления основной шкалы, деленной на число делений верньера. 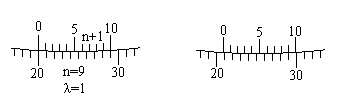 Рис.3.2 Рис.3.3 В практике очень часто встречается верньер на одну десятую, когда n = 9; точность такого верньера равна одной десятой деления основной шкалы. Роль отсчетного индекса в верньере выполняет его нулевой штрих. Если он совмещен с каким-либо штрихом основной шкалы, то отсчет по основной шкале равен значению этого штриха. Все остальные штрихи верньера не совпадают со штрихами основной шкалы; первый штрих верньера отстоит от ближайшего штриха основной шкалы на величину λ - μ = t, второй штрих верньера отстоит от ближайшего штриха основной шкалы на 2*t, третий - на 3*t и т.д. Если сейчас сместить верньер относительно основной шкалы на величину t, то со штрихом основной шкалы совпадет 1-й штрих верньера; если сместить верньер на 2*t, то со штрихом основной шкалы совпадет 2-й штрих верньера и т.д. Если сместить верньер на величину k*t, то со штрихом основной шкалы совпадет k-й штрих верньера, поэтому формула отсчета N по верньеру имеет вид (рис.3.3) N = Nмл + k*t, (3.4) где: Nмл - отсчет по младшему штриху основной шкалы,
k - номер штриха верньера, совпавшего со штрихом основной шкалы,
t - точность верньера. Чтобы не умножать на t, верньер подписывают в единицах основной шкалы. Например, для угловой шкалы при t = 30" подпись первого штриха 30", подпись второго штриха 1' и т.д. Наблюдатель считывает с основной шкалы значение младшего штриха Nмл, находит на шкале верньера штрих, совпавший со штрихом лимба, и считывает его значение k*t; складываются эти два отсчета в уме. Оптические отсчетные приспобления рассмотрим на примере угловой шкалы, расположенной на окружности; такая шкала называется угломерным кругом или лимбом. Ценой деления лимба λ называют центральный угол, стягиваемый дугой в одно деление; в практике встречаются лимбы с ценой деления 1o, 20', 10', 5'. Диаметр лимбов бывает от 72 мм до 270 мм. Роль отсчетного индекса при отсчете по лимбу могут выполнять одиночный штрих, двойной штрих (биссектор), нулевой штрих шкалы отсчетного приспособления, штрих основной шкалы (шкалы лимба). Штриховой микроскоп. Отсчетным индексом в штриховом микроскопе является неподвижный штрих, выгравированный на стеклянной пластинке, помещенной на пути хода лучей, идущих от осветитель ного окошка через штрихи лимба в отсчетный микроскоп. Оценка доли деления лимба выполняется на глаз. Из опыта установлено, что при отсчитывании на глаз наибольшая точность достигается при видимом расстоянии между штрихами 2.00 мм и толщине штрихов 0.10 мм; при таких условиях ошибка отсчета составляет 0.1 деления. Рассчитаем, с какой точностью можно взять на глаз отсчет по лимбу диаметром d=100 мм и разделенному на 360 частей: цена одного деления равна 1o. Периметр кольца делений равен π*d=314 мм; длина дуги в 1o l = 314 мм/360 = 0.9 мм. Если бы длина деления была равна 2 мм, то ошибка 0.1 деления соответствовала бы ошибке отсчитывания по шкале лимба 6'; при длине деления 0.9 мм ошибка отсчитывания будет примерно в 2 раза больше. Такой точности для измерения углов недостаточно, поэтому поступают следующим обра зом: делят градус на более мелкие деления и рассматривают их че рез микроскоп. Например, при диаметре лимба 72 мм и количестве делений на нем 2160 одно деление лимба равно 10'; увеличение микроскопа равно 18x, следовательно, видимая длина одного деления равна l = π*72*18 мм/2160 = 1.93 мм, и ошибка отсчитывания по лимбу будет 1'. В поле зрения окуляра штрихового микроскопа видны деления лимба и отсчетный индекс - штрих; отсчет по горизонтальному кругу (Г) равен 69o47', по вертикальному (В) - 358o150' (рис.3.4).  Рис.3.4 Рис.3.5 Шкаловой микроскоп. На пути хода лучей от осветительного окошка через штрихи лимба в поле зрения микроскопа помещена стеклянная пластинка с гравированной шкалой. Длина шкалы равна длине одного деления лимба λ; шкала разделена на n равных частей, цена одного деления шкалы шкалового микроскопа обозначается буквой μ и равна μ = λ / n . Отсчетным индексом является нулевой штрих шкалы шкалового микроскопа. Доля деления лимба от младшего штриха шкалы лимба до отсчетного индекса измеряется непосредственно по шкале микроскопа, так как направления возрастания делений на лимбе и на шкале микроскопа противоположные (рис.3.5). Доля деления шкалы микроскопа оценивается на глаз. Полный отсчет по лимбу равен сумме отсчетов по младшему штриху лимба Nмл и по шкале микроскопа Nш: N = Nмл + Nш. (3.5) На рис.3.5 отсчет по лимбу (λ=1o, n=60, μ=1' ) равен N = 20o + 54.3' = 20o 54.3'. При отсчете по шкале оптического отсчетного приспособления может появиться ошибка, причиной которой является рен. Рен - это разность между номинальным n и фактическим n' количеством делений шкалы отсчетного устройства, укладывающихся в одном делении (или полуделении) лимба; рен отсчетного устройства обозначается буквой r. Если совместить нулевой штрих шкалы шкалового микроскопа с каким-либо штрихом шкалы лимба, то n-й штрих шкалы должен точно совпасть с соседним штрихом лимба (рис.3.6-а). Но из-за мелких погрешностей при сборке и юстировке оптической системы прибора этого может и не быть (рис.3.6-б). Значение рена просто считывается по положению штриха лимба; на рис.3.6-б r = 1.5'; для удобства определения рена за пределами шкалы обычно имеются по два дополнительных деления. При заметном несовпадении n-ного штриха со штрихом лимба (r 0.1 деления шкалы микроскопа) прибор полагается сдать в мастерскую. 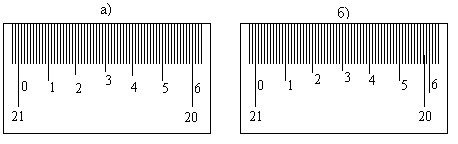 Рис.3.6 С конструкцией и принципом действия остальных отсчетных приспособлений можно ознакомиться в специальной литературе. 3.2 Зрительные трубы При многих геодезических измерениях приходится наблюдать далекие предметы или рассматривать очень мелкие деления. Разрешающая способность человеческого глаза ограничена; критический угол зрения у человека в среднем равен 60" (у разных людей он колеблется от 40" до 120"). Критическим углом называют предельный угол зрения, при котором две точки начинают сливаться в одну. Для увеличения угла зрения, когда он меньше критического значения, применяют различные оптические приспособления, одним из которых является зрительная труба. Зрительные трубы бывают астрономическими и земными. Астрономические трубы дают обратное, то-есть, перевернутое изображение предметов; земные трубы дают прямое изображение. В геодезических приборах чаще применяют астрономические трубы, так как они имеют более простое устройство и в них меньше потери света. По конструкции зрительные трубы бывают прямые и ломаные. Основными деталями зрительных труб являются линзы - стеклянные пластинки различной формы; линзы бывают собирательные и рассеивающие. Все собирательные линзы выпуклые: двояковыпуклые, плосковыпуклые, вогнутовыпуклые; все рассеивающие линзы вогнутые: двояковогнутые, плосковогнутые, выпукловогнутые. Линза имеет оптический центр; лучи, проходящие через него, не изменяют своего направления; все остальные лучи, проходя через линзу, испытывют преломление и изменяют свое первоначальное направление. Линия, соединяющая центры сферических поверхностей линзы, называется главной оптической осью линзы. По обе стороны от оптического центра на главной оптической оси есть точки, называемые главными фокусами линзы: передний фокус F и задний фокус F1. Расстояние от оптического центра до фокуса называется фокусным расстоянием. Если поместить в главный фокус точечный источник света, то лучи, пройдя через линзу, выйдут из нее пучком, параллельным главной оптической оси. И наоборот, пучок света, параллельный главной оптической оси, пройдя через линзу, собирается в точке главного фокуса. Плоскость, перпендикулярная главной оптической оси и проходящая через точку фокуса, называется фокальной плоскостью линзы. Для построения изображения предметов в линзе обычно используют три луча: луч, проходящий через оптический центр линзы, луч, идущий параллельно главной оптической оси, луч, проходящий через передний фокус линзы. Изображение считается действительным, если оно получается на пересечении лучей в прямом направлении; изображение считается мнимым, если оно получается на пересечении лучей в обратном направлении. Для всякой линзы справедлива формула: 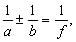 (3.6) (3.6)
где: a - расстояние от оптического центра до предмета,
b - расстояние от оптического центра до изображения предмета в линзе,
f - фокусное расстояние линзы.
При действительном изображении предмета в формуле нужно ставить знак "плюс", при мнимом - "минус". Ход лучей в трубе Кеплера. Астрономическая труба Кеплера является простейшей зрительной трубой; она состоит из двух собирательных линз - объектива и окуляра, имеющих общую главную оптическую ось, и корпуса; объектив трубы Кеплера - длиннофокусный, а окуляр - короткофокусный. При этом изображение, даваемое объективом, должно располагаться между передним фокусом окуляра и его оптическим центром; Построим в трубе Кеплера изображение отрезка BC, то-есть, нарисуем ход лучей от точек B и C, используя два из трех перечисленных выше лучей (рис.3.7). 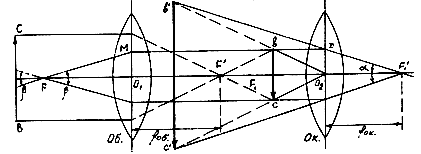 Рис.3.7. Объектив дает действительное обратное уменьшенное изображение предмета - отрезок bc. Изображение, даваемое окуляром, - мнимое, обратное, увеличенное - отрезок b'c'. Сам окуляр дает прямое изображение, но поскольку оно уже было обратным, то обратным и остается. Под увеличением трубы понимают отношение угла зрения, под которым изображение предмета видно в трубе, к углу зрения, под которым предмет виден невооруженным глазом, то-есть, без трубы. Обозначим первый угол через α, а второй - через β и напишем формулу увеличения трубы V =α / β . (3.7) Из треугольника DF'1O2 имеем: 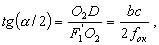 (3.8) (3.8) а из треугольника MO1F: 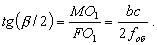 (3.9) (3.9) Углы α и β обычно малые, так как расстояние до предмета несравнимо больше размеров трубы, поэтому вместо тангенсов этих углов можно взять их значения в радианной мере: tg(α/2) = α/2 и tg(β/2) = β/2 , откуда следует, что отношение углов α и β равно отношению тангенсов их половинных значений: 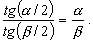 Подставим в эту формулу выражения тангенсов углов из (3.8) и (3.9) и получим: 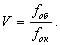 (3.10) (3.10) Увеличение трубы Кеплера равно отношению фокусного расстояния объектива к фокусному расстоянию окуляра. Высокоточные геодезические приборы имеют сменные окуляры с разными фокусными расстояниями, и смена окуляра позволяет изменять увеличение трубы в зависимости от условий наблюдений. Определение увеличения зрительной трубы с помощью рейки. Если навести трубу на близкостоящую рейку, то можно сосчитать, сколько делений рейки N, видимой невооруженным глазом, соответствуют n делениям рейки, видимой в трубу. Для этого нужно смотреть поочередно в трубу и на рейку, проектируя деления рейки из поля зрения трубы на рейку, видимую невооруженным глазом. Обозначим через γ угол, под которым видны n делений в трубу и N делений без трубы (рис.3.8). Тогда одно деление рейки видно в трубу под углом: α = γ / n, а без трубы - под углом: β = γ / N. 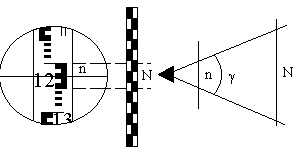 Рис.3.8 Отсюда: V = N / n . Этот способ определения увеличения трубы называется способом Галилея. Увеличение трубы можно приближенно вычислить по формуле: V = D / d, (3.11) где D - входной диаметр объектива; d - диаметр выходного отверcтия трубы (но не диаметр окуляра). Поле зрения трубы. Полем зрения трубы называют участок пространства, видимый в трубу при неподвижном ее положении. Поле зрения измеряют углом ε, вершина которого лежит в оптическом центре объектива, а стороны касаются краев отверстия диафрагмы (рис.3.9). Диафрагма диаметром d1 устанавливается внутри трубы в фокальной плоскости объектива.Из рисунка 3.11 видно, что: ![]() откуда 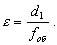 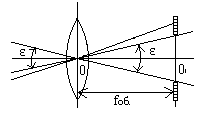 Рис.3.9. Обычно в геодезических приборах принимают d1 = 0.7 * fок, тогда в радианной мере: ε = 0.7 / V. Если ε выразить в градусах, то: ε = 40o / V . (3.12) Чем больше увеличение трубы, тем меньше ее угол зрения. Так, например, при V = 20x ε = 2o, а при V = 80x ε = 0.5o. Разрешающая способность трубы оценивается по формуле: 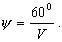 (3.13) (3.13) Например, при V = 20x ψ = 3"; под таким углом виден предмет размером 5 см на расстоянии 3.3 км; человеческий глаз может видеть этот предмет на расстоянии всего 170 м. Сетка нитей. Правильным наведением зрительной трубы на предмет считается такое, когда изображение предмета находится точно в центре поля зрения трубы. Чтобы исключить субъективный фактор при нахождении центра поля зрения, его обозначают сеткой нитей. Сетка нитей - это в простейшем случае два взаимно перпендикулярных штриха, нанесенных на стеклянную пластинку, которая крепится к диафрагме трубы. Сетка нитей бывает разных видов; на рис.3.10 показаны некоторые из них. Сетка нитей имеет исправительные винты: два боковых (горизонтальных) и два вертикальных. Линия, соединяющая центр сетки нитей и оптический центр объектива, называется визирной линией или визирной осью трубы. 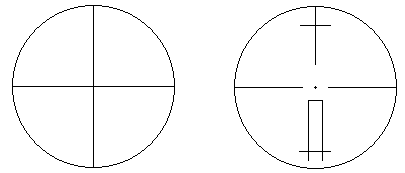 Рис.3.10 Установка трубы по глазу и по предмету. При наведении трубы на предмет нужно одновременно четко видеть в окуляре сетку нитей и изображение предмета. Установкой трубы по глазу добиваются четкого изображения сетки нитей; для этого передвигают окуляр относительно сетки нитей, вращая рифленое кольцо на окуляре. Установка трубы по предмету называется фокусированием трубы. Расстояние до рассматриваемых предметов бывает разным, и согласно формуле (3.6) при изменении a расстояние b до его изображения также меняется. Чтобы изображение предмета при рассматривании его в окуляр было четким, оно должно располагаться в плоскости сетки нитей. Передвигая окулярную часть трубы вдоль главной оптической оси, изменяют расстояние от сетки нитей до объектива до тех пор, пока оно станет равным b. Трубы, у которых фокусирование выполняется путем изменения расстояния между объективом и сеткой нитей, называются трубами с внешней фокусировкой. Такие трубы имеют большую и притом переменную длину; они негерметичны, поэтому внутрь них попадают пыль и влага; на близкие предметы они вообще не фокусируются. Зрительные трубы с внешней фокусировкой в современных измерительных приборах не применяются Более совершенными являются трубы с внутренней фокусировкой (рис.3.11); в них применяется дополнительная подвижная рассеивающая линза L2, образующая вместе с объективом L1 эквивалентную линзу L. При перемещении линзы L2 изменяется расстояние между линзами l и, следовательно, изменяется фокусное расстояние f эквивалентной линзы. Изображение предмета, находящееся в фокальной плоскости линзы L, также перемещается вдоль оптической оси, и когда оно попадает на плоскость сетки нитей становится четко видным в окуляре трубы. Трубы с внутренней фокусировкой короче; они герметичны и позволяют наблюдать близкие предметы;в современных измерительных приборах применяются в основном такие зрительные трубы. 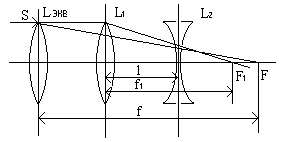 Рис.3.11 3.3 Уровни Уровни служат для приведения осей прибора в вертикальное или горизонтальное положение и для измерения малых углов наклона. Применение уровней основано на свойстве пузырька газа занимать в жидкости наивысшее положение. Уровни бывают цилиндрические и круглые. Цилиндрический уровень состоит из чувствительного элемента - ампулы и металлической оправы для ее крепления и защиты от внешних воздействий. Ампула цилиндрического уровня - это стеклянная трубка, запаянная с обоих концов и заполненная спиртом или серным эфиром; небольшое пространство занимают пары этой жидкости, оно называется пузырьком уровня. Ампула имеет форму дуги большого радиуса; касательная к дуге в середине пузырька всегда горизонтальна, так как выталкивающая сила, действующая на пузырек, направлена по вертикальной линии (пузырек принимает форму дуги окружности, выталкивающая сила на правлена по радиусу дуги, касательная перпендикулярна радиусу). На ампуле нанесены деления, на точных уровнях деления подписаны. Ценой деления уровня t называется центральный угол, соответствующий дуге в одно деление шкалы на ампуле. Точка O в середине шкалы называется нульпунктом уровня, а касательная, проведенная в нульпункте, называется осью цилиндрического уровня U-U (рис.3. 12). Если пузырек находится в нульпункте, то ось уровня занимает горизонтальное положение. Если пузырек уровня находится не в нульпункте, то ось уровня занимает наклонное положение. Чтобы приводить какую-либо линию или плоскость в горизонтальное положение, нужно закрепить уровень так, чтобы ось уровня была строго параллельной искомой линии или плоскости. Чтобы приводить линию или плоскость в вертикальное положение, нужно закрепить уровень так, чтобы ось уровня была строго перпендикулярна искомой линии или плоскости. Без выполнения этих условий применение уровня не имеет смысла. 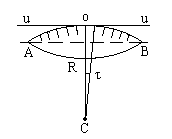 Рис.3.12 Если же условия выполняются, то при положении пузырька уровня в нульпункте ось уровня займет горизонтальное положение, а искомая линия или плоскость - горизонтальное положение в первом случае и вертикальное положение во втором случае. Внутренняя поверхность ампулы имеет форму, получающуюся при вращении дуги AB радиуса R вокруг хорды AB (рис.3.12). Радиус дуги R вычисляют по расчетной цене деления τ. Обозначив через l длину одного деления шкалы на ампуле, напишем формулу для длины дуги в функции центрального угла: 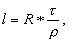 откуда 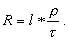 (3.14) (3.14) При τ = 10", l = 2 мм и ρ = 206265" получим R = 41 м. При наклоне уровня на угол ε пузырек отклонится от нульпункта на n деления, то есть, ε = n * τ . (3.15) Отсюда следует второе определение цены деления уровня: цена деления уровня - это угол, на который наклонится ось уровня при смещении пузырька на одно деление шкалы. Определение цены деления уровня по рейке. Из формулы (3.15) следует, что: τ = ε / n, т.е. для определения цены деления нужно знать угол ε и сосчитать число делений, на которое сместится пузырек (рис.3.13). Угол наклона ε можно определить разными методами, например, с помощью рейки. Наведем трубу на рейку и возьмем отсчеты: по рейке - b1 и по уровню. 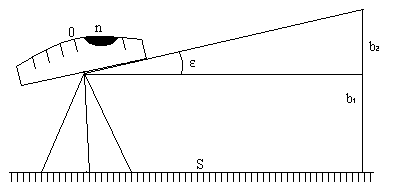 Рис.3.13 Затем немного наклоним трубу и снова возьмем отсчеты: по рейке - b2 и по уровню. Угол наклона ε вычисляется по формуле: 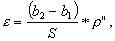 где S - расстояние от нивелира до рейке. Число делений уровня n, на которое переместился пузырек, подсчитывают по разности отсчетов по уровню при первом и втором наведениях на рейку. Более точное определение цены деления уровня производят на специальном устройстве - экзаменаторе; при этом одновременно выполняют исследование качества шлифовки внутренней поверхности ампулы уровня. По конструкции цилиндрические уровни бывают простыми, компенсированными и камерными. У простых уровней ампула заполнена жидкостью и имеет один пузырек. У компенсированных уровней внутри ампулы помещена стеклянная трубка с запаянными концами. При изменении температуры объемы жидкости и пузырька газа изменяются неодинаково вследствие разных коэффициентов расширения. Это приводит к тому, что при понижении температуры пузырек удлиняется, при повышении - укорачивается. Наличие стеклянной трубки в ампуле уменьшает объем жидкости, и поэтому влияние изменения температуры на длину пузырька ослабляется. У камерных уровней внутри ампулы есть перегородка с отверстием внизу, которая делит ампулу на две камеры - основную и запасную. Запасная камера намного меньше по объему, и в ней помещается запасной пузырек. При изменении длины основного пузырька наклоняют уровень и либо убирают часть пузырька в запасную камеру, либо добавляют некоторое количество газа из запасной камеры. Согласно Инструкции [18] длина пузырька должна составлять 0.4 - 0.5 длины шкалы на ампуле. По точности уровни бывают малой точности (τ 1'), средней точности (5" Круглый уровень - это часть стеклянной сферы, на которую нанесены концентрические окружности. Центр окружностей является нульпунктом круглого уровня. Осью круглого уровня называется нормаль к сферической поверхности ампулы, проведенная в нульпункте. Если пузырек уровня находится в нульпункте, то его ось занимает вертикальное (отвесное) положение. Круглые уровни относятся к уровням малой точности. Поверка установки цилиндрического уровня. Пусть цилиндрический уровень предназначен для приведения в вертикальной положение оси вращения геодезического прибора; тогда условие их взаимного положения читается так: ось уровня должна быть перпендикулярна оси вращения прибора.Теоретическое положение оси уровня и оси вращения прибора изображено на рис.3.14; на нем UU1 - ось уровня, ZZ1 - ось вращения прибора, она вертикальна и составляет с осью уровня угол 90o; пузырек уровня находится в нульпункте. При повороте прибора вокруг своей оси ось уровня описывает в пространстве горизонтальную плоскость, и после поворота прибора на 180o пузырек остается в нульпункте. 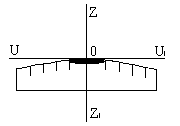 Рис.3.14 Пусть угол между осью уровня и осью вращения прибора равен не точно 90o, а (90o - i) (рис.3.15). Если установить прибор так, чтобы пузырек уровня был в нульпункте, то ось уровня займет горизонтальное положение, а ось вращения прибора будет наклонена на угол i относительно своего правильного положения. Задача поверки - найти угол i и устранить его. Повернем прибор на 180o (рис.3.16). Ось уровня опишет коническую поверхность с углом при вершине конуса 180o-2i и займет не горизонтальное положение, а наклонится относительно горизонта на угол 2i; пузырек отклонится от нульпункта на n делений, следовательно, 2 * i = n * τ , откуда  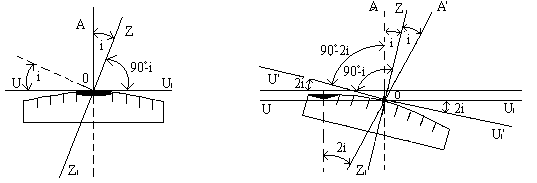 Рис.3.15 Рис.3.16 Чтобы условие выполнялось, нужно, во-первых, изменить угол между осью уровня и осью вращения прибора на величину i и, во-вторых, наклонить прибор также на угол i. Практически поступают так: сначала подъемными винтами наклоняют прибор на угол i; при этом пузырек должен приблизиться к нульпункту на половину отклонения. Затем, пользуясь исправительными винтами уровня, изменяют положение ампулы в корпусе прибора; при этом пузырек должен установиться точно в нульпункте. Таким образом, последовательность действий при поверке установки уровня следующая: Вращая прибор, установить уровень параллельно двум подъемным винтам. Этими подъемными винтами привести пузырек уровня в нульпункт. Повернуть прибор точно на 180o. Сосчитать количество делений n отклонения пузырька уровня от нульпункта. Подъемными винтами сместить пузырек обратно на n/2 делений. Исправительными винтами уровня привести пузырек в нульпункт. Если угол i большой, то после поворота прибора на 180o пузырек уходит за пределы шкалы, и количество делений n сосчитать нельзя. В этом случае отклонение пузырька от нульпункта можно измерить в более крупных единицах, например, в оборотах подъемных винтов, и исправлять уровень способом последовательных приближений. Существуют и другие способы исправления уровня; один из них - способ Г.Лысова - позволяет исправить сильно разъюстированный уровень за одно приближение. Последовательность операций в способе Г.Лысова. Умеренно вывернуть (или завернуть) любой из подъемных винтов, чтобы наклон прибора был заметен глазом (i 1o). Плавно вращая прибор, зафиксировать такое его положение, при котором пузырек уровня находится точно в нульпункте; взять отсчет по горизонтальному лимбу N1. Плавно вращая прибор, зафиксировать второе его положение, при котором пузырек уровня также находится точно в нульпункте; взять отсчет по горизонтальному лимбу N2. Вычислить отсчет N = 0.5 (N1 + N2) + 90o и, плавно вращая прибор, установить его на горизонтальном лимбе. Исправительными винтами уровня привести пузырек в нульпункт. Устройство теодолита Прибор для измерения на местности горизонтальных и вертикальных углов называется теодолитом. У первых теодолитов в центре угломерного круга на острие иголки помещалась линейка, которая могла свободно вращаться на этом острие (как стрелка у компаса); в линейке были сделаны вырезы и в них натянуты нити, играющие роль отсчетных индексов. Центр угломерного круга помещали в вершину измеряемого угла и надежно его закрепляли. Поворачивая линейку, совмещали ее с первой стороной угла и брали отсчет N1 по шкале угломерного круга. Затем совмещали линейку со второй стороной угла и брали отсчет N2. Разность отсчетов N2 и N1 равна значению угла. Подвижная линейка называлась алидадой, а сам угломерный круг назывался лимбом. Для совмещения линейки-алидады со сторонами угла применялись примитивные визиры. Современные теодолиты, сохранив идею измерения угла, конструктивно значительно отличаются от старинных теодолитов. Во-первых, для совмещения алидады со сторонами угла используется зрительная труба, которую можно вращать по высоте и по азимуту; во-вторых, для отсчета по шкале лимба имеется отсчетное приспособление, в третьих, вся конструкция теодолита закрыта прочным металлическим кожухом и т.д. Для плавного вращения алидады и лимба имеется система осей, а сами вращения регулируются зажимными и наводящими винтами. Для установки теодолита на земле применяется специальный штатив, а совмещение центра лимба с отвесной линией, проходящей через вершину измеряемого угла, осуществляется с помощью оптического центрира или нитяного отвеса. Стороны измеряемого угла проектируются на плоскость лимба подвижной вертикальной плоскостью, которая называется коллимационной плоскостью. Коллимационная плоскость образуется визирной осью зрительной трубы при вращении трубы вокруг своей оси. Визирная ось трубы (или визирная линия) - это воображаемая линия, проходящая через центр сетки нитей и оптический центр объектива трубы. Перечислим основные части теодолита (рис.4.4): Лимб - угломерный круг с делениями от 0o до 360o; при измерении углов лимб является рабочей мерой (на рис.4.4 не показан). Алидада - подвижная часть теодолита, несущая систему отсчитывания по лимбу и визирное устройство - зрительную трубу. Обычно всю вращающуюся часть теодолита называют алидадной частью или просто алидадой (2 на рис.4.4). Зрительная труба крепится на подставках на алидадной части (3). Система осей - обеспечивает вращение алидадной части и лимба вокруг вертикальной оси. Вертикальный круг служит для измерения вертикальных углов (4). Подставка с тремя подъемными винтами (5). Зажимные и наводящие винты вращающихся частей теодолита: лимба (8,9), алидады (6,7), трубы (10,11); зажимные винты называют также закрепительными и стопорными, а наводящие - микрометренными. Штатив с крючком для отвеса, площадкой для установки подставки теодолита и становым винтом.
12 - винт перестановки лимба;
13 - уровень при алидаде горизонтального круга;
14 - уровень вертикального круга;
15 - винт фокусировки трубы;
16 - окуляр микроскопа отсчетного устройства.   Рис.4.4 В теодолитах различают три разных вращения: вращение зрительной трубы, вращение алидады и вращение лимба; при этом вращение трубы и вращение алидады снабжаются двумя винтами каждое - зажимным и наводящим. Что касается вращения лимба, то оно оформляется по-разному. В повторительных теодолитах лимб может вращаться только вместе с алидадой; в теодолите Т30 (2Т30 и т.п.) для вращения лимба имеются два винта: зажимной и наводящий, причем они работают только при зажатом винте алидады. В теодолите Т15 первых выпусков лимб скреплялся с алидадой с помощью специальной защелки и в таком положении совместное вращение алидады и лимба регулировалось винтами алидады. В точных и высокоточных теодолитах вращение (перестановка) лимба выполняется специальным бесконечным винтом (позиция 12 на рис.4.4-б). 4.1.3. Поверки и исследования теодолита Теодолит как прибор для измерения углов должен удовлетворять некоторым геометрическим условиям, вытекающим из общего принципа измерения горизонтального угла. Рассмотрим эти условия: 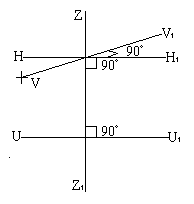 Рис.4.5 Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к оси вращения алидады. Ось вращения алидады должна быть установлена отвесно (вертикально). Визирная ось трубы должна быть перпендикулярна к оси вращения трубы. Ось вращения трубы должна быть перпендикулярна к оси вращения алидады. Вертикальная нить сетки нитей должна лежать в коллимационной плоскости. Для всех этих условий, кроме второго, обязательно выполняются поверки для того, чтобы выяснить удовлетворяет ли конкретный теодолит перечисленным условиям. Если при выполнении поверок обнаруживается, что какое-либо условие не выполняется, производят исправление теодолита. Поверка первого условия была рассмотрена в разделе 3.3; следует лишь подчеркнуть, что исправление угла между осью уровня и осью вращения алидады производится исправительными винтами уровня. Установка оси вращения алидады в вертикальное положение выполняется в следующем порядке: вращая алидаду, устанавливают уровень параллельно линии, соединяющей два подъемных винта и приводят пузырек уровня в нульпункт, действуя этими двумя винтами, вращают алидаду на 90o, то есть, устанавливают уровень по направлению третьего подъемного винта, и, действуя этим винтом, приводят пузырек уровня в нульпункт. После этого вращают алидаду и устанавливают ее в произвольное положение; пузырек уровня должен оставаться в нульпункте. Если пузырек уровня отклоняется от нульпункта больше, чем на одно деление, следует заново выполнить первую поверку и снова установить ось вращения алидады в вертикальное положение. Процедура установки оси вращения алидады в вертикальное положение называется горизонтированием теодолита. Поверка перпендикулярности визирной оси трубы к оси вращения трубы. Эта поверка выполняется с помощью отсчетов по горизонтальному кругу при наблюдении какой-либо визирной цели. Если условие выполняется, то при вращении трубы вокруг своей оси визирная линия трубы описывает плоскость, совпадающую с коллимационной плоскостью. Если угол между визирной линией трубы и осью вращения трубы не равен точно 90o, то при вращении трубы визирная линия будет описывать коническую поверхность с углом при вершине конуса 180o - 2С, где С - угол между фактическим положением визирной линии трубы и ее теоретическим положением; угол С называется коллимационной ошибкой (рис.4.6). 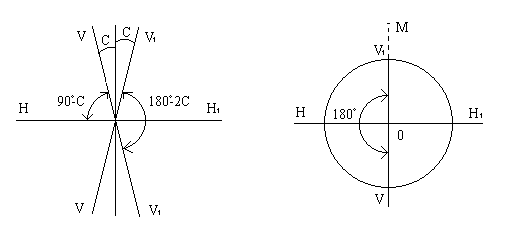 Рис.4.6 Рис.4.7 Навести трубу на точку можно при двух положениях вертикального круга: круг слева и круг справа; эти положения называются "круг лево" - КЛ или L и "круг право" - КП или R. Пусть при положении КЛ отсчет по лимбу будет NL. Для наведения трубы на точку при КП нужно перевести трубу через зенит и повернуть алидаду на 180o. Если С = 0, то алидаду нужно повернуть точно на 180o, то-есть, разность отсчетов при КЛ и КП равна точно 180o (рис.4.7). Если С= 0, то при том же положении алидады изображение точки будет находиться не в центре сетки нитей и для наведения на точку нужно повернуть алидаду на угол С (рис.4.8). Отсчет по лимбу изменится и, если правильный отсчет был NL, то отсчет, искаженный коллимационной ошибкой, будет N'L = NL + C, а NL = N'L - C. (4.2) 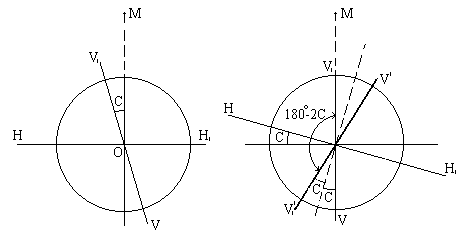 Рис.4.8 Рис.4.9 Чтобы навести трубу на точку при КП, нужно перевести ее через зенит и повернуть алидаду на угол 180o - 2C (рис.4.9), отсчет по лимбу будет равен: NR' = NL + C + 180o - 2C = NR - C. (4.3) Таким образом, можно написать: NL' = NL + C, NR' = NR - C. Средний отсчет из отсчетов при КЛ и КП свободен от влияния коллимационной ошибки, 0.5 * (NL' + NR') = 0.5 * (NL + NR), а значение двойной коллимационной ошибки равно: 2C = NL' - NR' + 180o. (4.4) В теодолитах с односторонним отсчитыванием по лимбу в каждом отдельном отсчете (и при КЛ и при КП) присутствует еще ошибка эксцентриситета алидады, поэтому значение коллимационной ошибки, подсчитанное по формуле (4.4), будет включать ошибку эксцентриситета. Для таких теодолитов (Т30, Т15, Т5) коллимационную ошибку определяют по более сложной методике, состоящей из следующих действий: навести трубу при КЛ на четко видимую точку, расположенную вблизи горизонта, взять отсчет по лимбу NL', перевести трубу через зенит, навести ее на ту же точку при КП и взять отсчет по лимбу NR', ослабить зажимной винт подставки и повернуть теодолит относительно подставки примерно на 180o, навести трубу на точку при КЛ, взять отсчет NL", навести трубу на точку при КП, взять отсчет NR", вычислить коллимационную ошибку по формуле: 2C = 0.5 * [(NL' + NL") - (NR' + NR") + 360o. (4.5) Исправление коллимационной ошибки, если она больше допустимого значения, производится одинаковым для большинства теодолитов способом: NL = NL' - C, или NR = NR' + C и устанавливают его на лимбе. При этом изображение точки не будет совпадать с центром сетки нитей на величину С. Боковыми исправительными винтами сетки нитей совмещают центр сетки нитей с изображением точки. После этого повторяют определение 2С. Влияние коллимационной ошибки на отсчет по лимбу. При наблюдении точек, расположенных вблизи плоскости горизонта, отсчет по лимбу искажается на величину коллимационной ошибки С с одним знаком при КЛ и с другим знаком при КП. Но иногда приходится наблюдать точки, которые располагаются выше или ниже плоскости горизонта, а при астрономических наблюдениях трубу теодолита наводят на звезды, устанавливая ее на любой угол наклона. Рассмотрим, как искажается отсчет по лимбу из-за влияния коллимационной ошибки в общем случае. На рис.4.10 точка O - точка пересечения оси вращения трубы HH1и визирной линии трубы. Труба направлена на высокорасположенную точку W; угол наклона визирной линии трубы - ν. Проведем через точку W вспомогательную вертикальную плоскость; LL1 - это линия пересечения этой плоскости с плоскостью горизонта точки О. 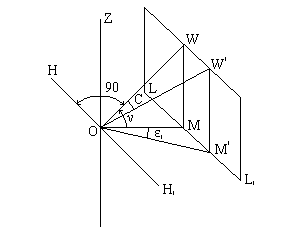 Рис.4.10 При С=0 визирная линия трубы занимает положение OW и коллимационная плоскость пересекает плоскость горизонта по линии OM. При наличии коллимационной ошибки визирная линия трубы займет положение OW'. Коллимационная плоскость в этом случае пересекает плоскость горизонта по линии OM'. Чтобы навести трубу на точку W, нужно повернуть алидаду на угол ε1, и отсчет по лимбу изменится на величину этого угла. Из треугольника MOM' выразим тангенс угла ε1: 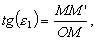 и по малости его запишем: 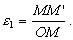 Но MM' = WW', поэтому 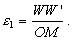 (4.6) (4.6) Из треугольника WOW' найдем тангенс угла С и вследствие малости угла С напишем: 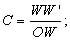 отсюда выразим длину отрезка WW': WW' = C * OW (4.7) и, подставив это выражение в формулу (4.6), получим: 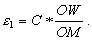 (4.8) (4.8) Из треугольника WOM видно, что: 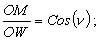 подставив это выражение в формулу (4.8), получим окончательно: 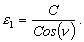 (4.9) (4.9) Если угол наклона трубы ν небольшой, то косинус этого угла мало отличается от единицы и ε1 = C. Обычно каждую точку наблюдают при двух положениях круга, и средний отсчет свободен от влияния коллимационной ошибки. Поверка перпендикулярности оси вращения трубы к оси вращения алидады. Четвертое условие обеспечивает вертикальное положение коллимационной плоскости. Для проверки этого условия используют хорошо видимую высоко расположенную точку М. Сначала наводят трубу на точку при КЛ и проектируют точку на уровень горизонта теодолита зрительной трубой; отмечают точку m1 (рис.4.11). Затем переводят трубу через зенит, наводят ее на точку при КП и снова проектируют точку на уровень горизонта теодолита; отмечают точку m2. Если ось вращения трубы перпендикулярна оси вращения алидады, то проекция точки М оба раза попадет в точку m; в противном случае точек будет две - m1 и m2. Положение, при котором один конец оси трубы выше другого, возникает, когда высота подставок трубы неодинакова; вследствие этого рассматриваемую поверку иногда называют поверкой неравенства подставок. 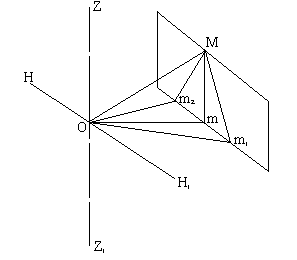 Рис.4.11 Для исправления угла между осями HH1 и ZZ1 нужно изменить высоту той подставки, которая имеет исправительный винт. Исправление неравенства подставок выполняется методом последовательных приближений. Если теодолит не имеет исправительного винта подставки, то при обнаружении неравенства подставок его нужно сдать в мастерскую. Влияние неравенства подставок на отсчет по лимбу. Пусть ось вращения трубы HH1 наклонена к горизонту на угол i и занимает положение H'H'1 (рис.4.12). Если бы наклона не было, то точка М проектировалась бы в точку m. При наклоне оси точка М проектируется в точку m1, и ошибка отсчета по лимбу будет равна углу ε2. Определим величину этого угла.  Рис.4.12 Из треугольника mOm1 следует:  или по малости угла ε2:  (4.10) (4.10) Из треугольника mMm1, в котором угол при точке M равен i, находим: 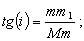 по малости угла i принимаем tg(i) = i, поэтому 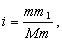 откуда mm1 = i * Mm . (4.11) Подставим (4.11) в (4.10) и получим: 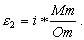 (4.12) (4.12) Из треугольника MOm выразим тангенс угла ν: 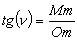 и,подставив это выражение в (4.12), получим окончательно: ε2 = i * tg(ν) . (4.13) При ν = 0 влияние неравенства подставок равно нулю при любых значениях угла i. Если ось вращения трубы наклонена к горизонту из-за неравенства подставок, то наклон коллимационной плоскости имеет противоположные знаки при КЛ и КП, и ошибка отсчета тоже имеет противоположные знаки; в среднем отсчете ошибка ε2 исключается. Влияние наклона оси вращения алидады на отсчет по лимбу. Наклон оси ZZ1 на угол i приводит к тому, что ось вращения трубы будет наклонена к горизонту на тот же угол (рис.4.13); коллимационная плоскость отклонится от вертикального положения на тот же угол. Следовательно, и влияние наклона оси вращения алидады аналогично влиянию неравенства подставок. Различие состоит в том, что ошибка в отсчете по лимбу из-за наклона оси вращения алидады имеет один и тот же знак при КЛ и КП. Таким образом, и средний отсчет также содержит эту ошибку. Для ослабления влияния наклона оси вращения алидады следует как можно тщательнее выполнять горизонтирование теодолита и следить за пузырьком уровня во время работы. При точных измерениях углов для исключения этой ошибки определяют угол i из дополнительных отсчетов по шкале уровня и вводят в отсчеты по лимбу поправки, вычисляемые по формуле (4.13). 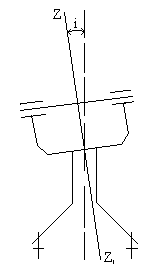 Рис.4.13 Поверка сетки нитей. Поверка пятого условия выполняется последней. Наводят трубу на хорошо видимую точку и наводящим винтом смещают ее по высоте. Если при этом изображение точки остается на вертикальной нити сетки нитей, то условие выполняется. Если изображение точки сходит с вертикальной нити, нужно ослабить исправительные винты сетки нитей и развернуть сетку в нужном направлении. После этого следует повторить поверку и снова определить коллимационную ошибку, так как при ослаблении и затягивании исправительных винтов сетки нитей ее центр мог сдвинуться в сторону. Кроме геометрических условий у теодолита проверяют так называемые механические условия: отсутствие механических повреждений - изломов, изгибов, трещин и т.п.; это проверяется путем внешнего осмотра, при котором следует удостовериться и в полной комплектности прибора; плавность вращения всех вращающихся деталей, то-есть, отсутствие заеданий, тугого вращения, скрипа и стука; плавность и легкость работы зажимных винтов; плавность и равномерность работы наводящих винтов; равномерность и легкость работы подъемных винтов. Эксцентриситет алидады. В плоскости лимба горизонтального круга имеются три характерных точки: D - центр круга делений лимба, A - центр вращения алидады, L - центр вращения лимба (рис.4.14). В идеальном теодолите все три точки должны совпадать, но в действительности они не совпадают. Несовпадение точки A с точкой D называется эксцентриситетом алидады, несовпадение точки L с точкой D называется эксцентриситетом лимба, несовпадение точек A и L называется эксцентриситетом осей. Рассмотрим влияние эксцентриситета алидады на отсчеты по лимбу. Отрезок AD называется линейным элементом эксцентриситета алидады и обозначается буквой l. 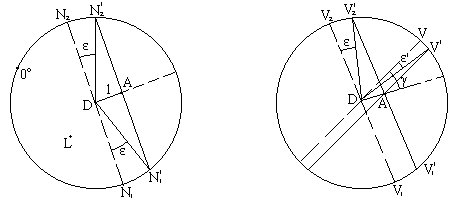 Рис.4.14 Рис.4.15 Некоторые теодолиты имеют два отсчетных устройства, отстоящих одно от другого на 180o. Вследствие эксцентриситета алидады отсчет по одному отсчетному индексу будет меньше правильного отсчета на угол ε: N'1 = N1 - ε, (4.14) а по другому отсчетному индексу - больше правильного на угол ε: N'2 = N2 + ε. (4.15) Средний отсчет будет свободен от влияния эксцентриситета: N = 0.5*(N1' + N2') = 0.5*(N1 + N2) . Чтобы получить численное значение эксцентриситета, нужно из отсчета N2' (4.15) вычесть отсчет N1' (4.14): N2' - N1' = N2 - N1 + 2*ε, но N2 - N1 = 180o, поэтому: ε = 0.5*(N'2 - N'1 + 180o). (4.16) При вращении алидады взаимное положение линейного элемента эксцентриситета алидады и отсчетных индексов изменяется, и величина ошибки отсчета ε' зависит от угла γ (рис.4.15): ε' = ε * Sin(γ) . (4.17) У теодолитов с односторонним отсчитыванием отсчет по лимбу искажается на величину ε' с одним знаком при КЛ и с другим знаком при КП; в среднем отсчете влияние эксцентриситета исключается. Из всех ошибок отсчитывания по лимбу, возникающих вследствие нарушения геометрических условий, можно выделить симметричные ошибки, то есть такие, которые имеют разные знаки при КЛ и КП и влияние которых в среднем отсчете устраняется, и несимметричные ошибки, влияние которых в среднем отсчете не устраняется. К симметричным ошибкам относятся коллимационная ошибка, ошибка из-за неравенства подставок, ошибка эксцентриситета. К несимметричным ошибкам относятся ошибка наклона оси вращения алидады, ошибки делений лимба и некоторые другие. |