Квадрат те?деулерді шешу ?дістері

Просмотр содержимого документа
«Квадрат те?деулерді шешу ?дістері»

8 сынып

Та?ырыбы: Квадрат те?деулерді шешу.

Ма?саты:

Та?ырып бойынша негізгі білім мен біліктілікті жина?тау,?орытындылау
Логикалы? ойлауын,еске са?тауын дамыту;
Е?бекс?йгіштікке,?зара к?мекке,бір-бірін сыйлау?а т?рбиелеу

Саба?ты? ж?рісі:

1.?йымдастыру

?рбір бала?а н?тижелік карта ?лестіріледі.Оны бала толтырады.

Аты ж?ні

Сергіту

Тест

Теориядан с?ра?

Те?деу шешу

?з бетімен ж?мыс

?орытынды

?пай саны

2.Ауызша ж?мыс. ?рбір д?рыс жауап?а 1 ?пай ?ояды.

Екінші д?режелі те?деу ?алай аталады?
Квадрат те?деуді? т?бірі неге байланысты?
ХХІ ?асыр ?ашан басталды?
D 0- ден ?лкен болса,те?деуді? неше т?бірі бар?
Айнымалысы бар те?дік
Білімді ба?алайтын нашар ба?а?
Те?деу шешу дегеніміз не?
Шаманы? жо?ты?ын к?рсететін цифр.
Бірінші коэффициенті 1 болатын квадрат те?деу.
1 жылда к?н неше рет шы?ады?
Дискриминанат 0-ден кіші болса, квадрат те?деуді? неше т?бірі бар.

3. Тест «Квадрат те?деуді? т?рлері»

Аты ж?ні

Толы?

Толым

сыз

Келтір

ілген

Келтіріл

меген

Биква

драт

Жалпы ?пай

1. х4 + 5х2 +3 = 0

2. 6х2 + 9 = 0

3. х2 – 3х = 0

4. –х2 + 2х +4 = 0

5. 3х + 6х2 + 7 =0

Ба?алау: ?ате жо?-5?пай,1-2 ?ате-4?пай, 3-4 ?ате-3 ?пай,5-6 ?ате -2

О?ушылар кілт бойынша бір –бірін тексереді.

4.?з бетімен ж?мыс

А-тобы ?р д?рыс жауап 1 ?пай,В тобы ?р д?рыс жауап-2 ?пай, С тобы ?р д?рыс жауап-3 ?пай.

1-н?с?а

А де?гей

№1. ?рбір те?деуі ?шін м?ндерін ата

а) б)

№2. квадрат те?деуіні? дискриминантын формуласын есептеуді жал?астыр.

5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;

№3. Те?деуді шешуді ая?та. 3х2 - 5х – 2 = 0.

D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…

В де?гей.Те?деуді шеш: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.

С де?гей . Те?деуді шеш:

а) -5х2 – 4х + 28 = 0; б) 2х2–8х–2=0. x1=2+, x2=2–

?осымша тапсырма. а –ны? ?андай м?нінде х2 - 2ах + 3 = 0 те?деуіні? бір т?бірі бар болады?

2 н?с?а.

А де?гей

№1. ?рбір ax2 + bx + c = 0 те?деуі ?шін a, b, c м?нін табы?дар.

а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0

№2. №2. квадрат те?деуіні? дискриминантын формуласын есептеуді жал?астыр.

5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;

№3. Те?деуді шешуді ая?та х2 - 6х + 5 = 0.

D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…

В де?гей. Те?деуді шеш : а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.

С де?гей. Те?деуді шеші?дер:

а) 5х2 + 4х - 28 = 0; б) х2 – 6х + 7 = 0; x1=3+, x2=3–.

?осымша тапсырма. а –ны? ?андай м?нінде х2 + 3ах + а = 0 те?деуіні? бір т?бірі бар болады?

Ба?алау шектері 15 – 20 ?пай – “5”. 9 – 14 ?пай – “4”. 5 - 8 ?пай – “3”.

5.Саба?ты ?орытындылау

6.Ба?алау

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Толым

сыз

Келтір

ілген

Келтіріл

меген

Биква

драт

Жалпы ұпай

1. х⁴+ 5х²+3 = 0

2. 6х²+ 9 = 0

3. х² – 3х = 0

4. –х² + 2х +4 = 0

5. 3х + 6х² + 7 =0

8 сынып

Тақырыбы: Квадрат теңдеулерді шешу.

Мақсаты:

Тақырып бойынша негізгі білім мен біліктілікті жинақтау,қорытындылау
Логикалық ойлауын,еске сақтауын дамыту;
Еңбексүйгіштікке ,өзара көмекке,бір-бірін сыйлауға тәрбиелеу

Сабақтың жүрісі:

1.Ұйымдастыру

Әрбір балаға нәтижелік карта үлестіріледі.Оны бала толтырады.

Аты жөні	Сергіту	Тест	Теориядан сұрақ	Теңдеу шешу	Өз бетімен жұмыс	Қорытынды
Ұпай саны

2.Ауызша жұмыс. Әрбір дұрыс жауапқа 1 ұпай қояды.

Екінші дәрежелі теңдеу қалай аталады?
Квадрат теңдеудің түбірі неге байланысты?
ХХІ ғасыр қашан басталды?
D 0- ден үлкен болса,теңдеудің неше түбірі бар?
Айнымалысы бар теңдік
Білімді бағалайтын нашар баға?
Теңдеу шешу дегеніміз не?
Шаманың жоқтығын көрсететін цифр.
Бірінші коэффициенті 1 болатын квадрат теңдеу.
1 жылда күн неше рет шығады?
Дискриминанат 0-ден кіші болса, квадрат теңдеудің неше түбірі бар.

3. Тест «Квадрат теңдеудің түрлері»

Бағалау: Қате жоқ-5ұпай,1-2 қате-4ұпай, 3-4 қате-3 ұпай,5-6 қате -2

Оқушылар кілт бойынша бір –бірін тексереді.

1.	+		+		+
2.		+		+
3.		+	+
4.	+			+
5.	+			+

4.Өз бетімен жұмыс

А-тобы әр дұрыс жауап 1 ұпай,В тобы әр дұрыс жауап-2 ұпай, С тобы әр дұрыс жауап-3 ұпай.

1-нұсқа

А деңгей

№1 . Әрбір 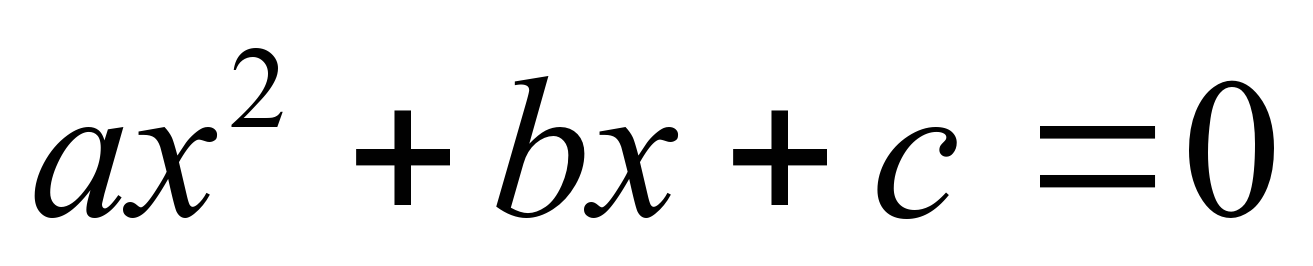теңдеуі үшін 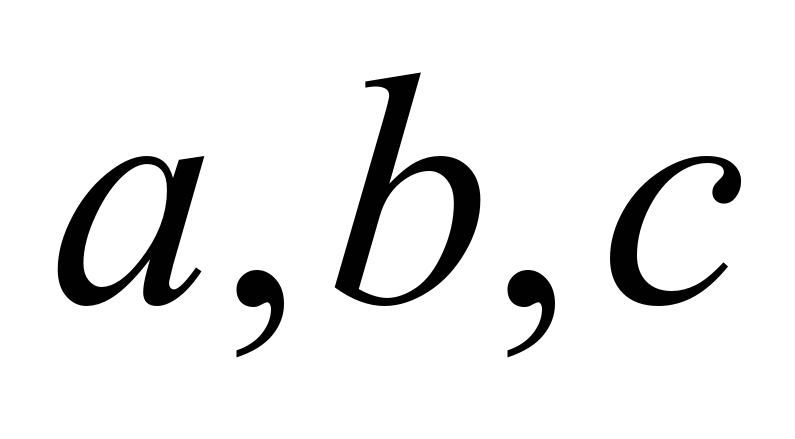мәндерін ата

а) 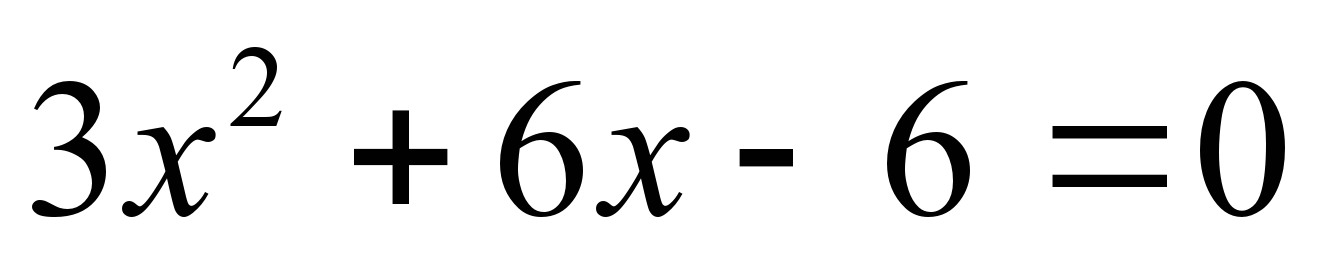б)

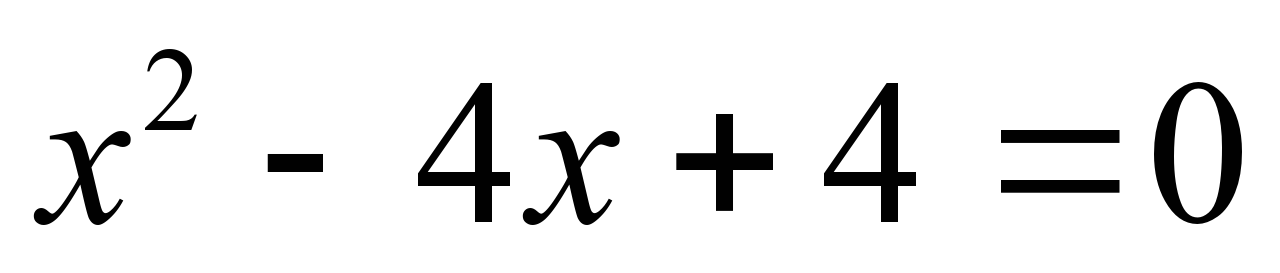№2 . 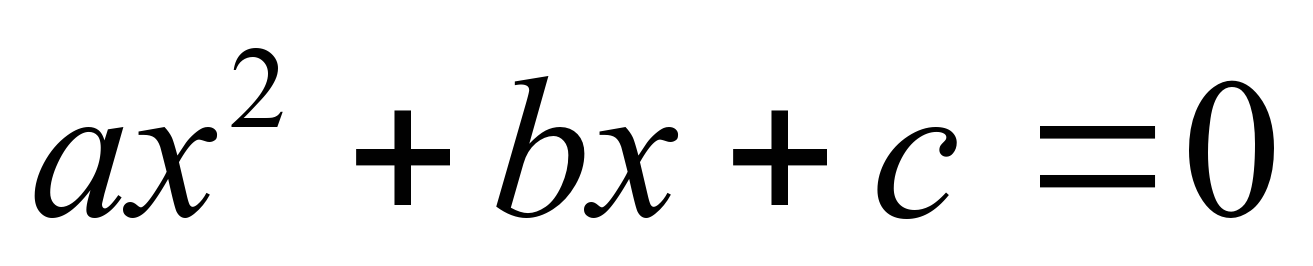квадрат теңдеуінің дискриминантын 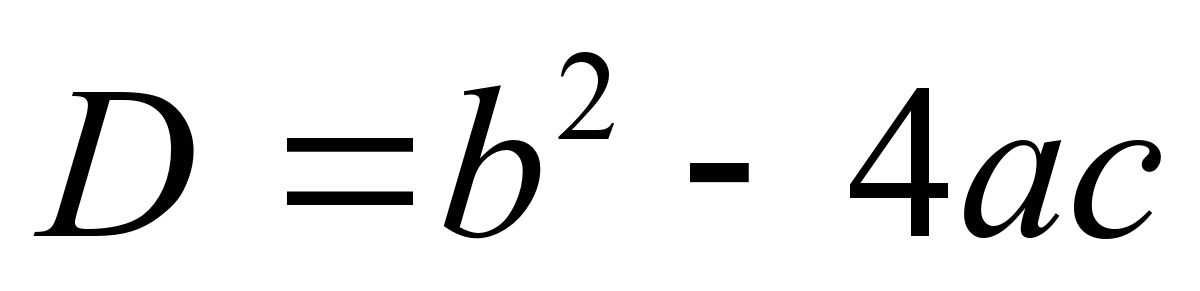формуласын есептеуді жалғастыр.

5х² - 7х + 2 = 0, D = b² - 4ac = (-7)² – 4· 5 · 2 = …;

№3. Теңдеуді шешуді аяқта. 3х² - 5х – 2 = 0.

D = b² - 4ac = (-5)²- 4· 3·(-2) = 49; х₁= … х₂=…

В деңгей .Теңдеуді шеш: а) 6х²– 4х + 32 = 0; б) х² + 5х - 6 = 0.

С деңгей . Теңдеуді шеш:

а) -5х²– 4х + 28 = 0; б) 2х²–8х–2=0. x₁=2+, x₂=2–

Қосымша тапсырма. а –ның қандай мәнінде х² - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?

2 нұсқа.

А деңгей

№1. Әрбір ax² + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.

а) 4х² - 8х + 6 = 0, б) х² + 2х - 4 = 0

№2. №2 . 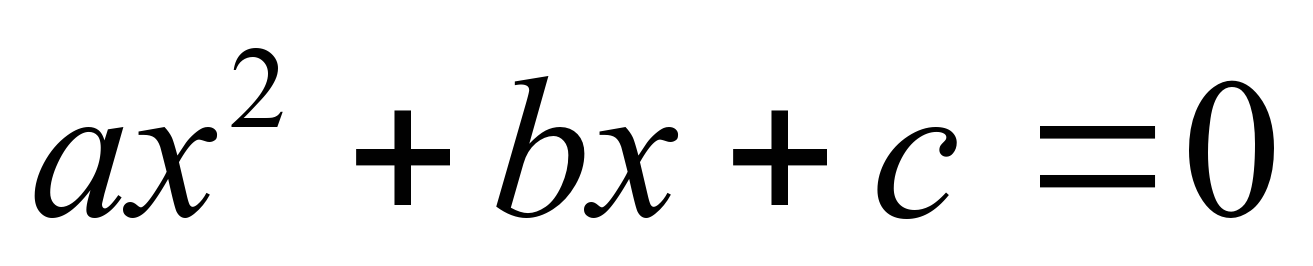квадрат теңдеуінің дискриминантын 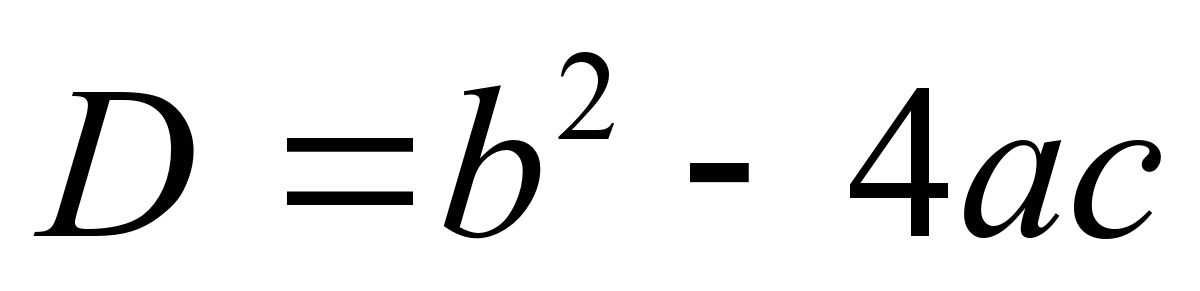формуласын есептеуді жалғастыр.

5х² + 8х - 4 = 0, D = b² - 4ac = 8² – 4· 5 · (- 4) = …;

№3. Теңдеуді шешуді аяқта х² - 6х + 5 = 0.

D = b² - 4ac = (-6 )² - 4· 1·5 = 16; х₁= … х₂=…

В деңгей. Теңдеуді шеш : а) 3х²– 2х + 16 = 0; б) 3х² - 5х + 2 = 0.

С деңгей. Теңдеуді шешіңдер:

а) 5х²+ 4х - 28 = 0; б) х²– 6х + 7 = 0; x₁=3+, x₂=3–.

Қосымша тапсырма. а –ның қандай мәнінде х² + 3ах + а = 0 теңдеуінің бір түбірі бар болады?

Бағалау шектері 15 – 20 ұпай – “5”. 9 – 14 ұпай – “4”. 5 - 8 ұпай – “3”.

5.Сабақты қорытындылау

6.Бағалау

А тобы.

№1 . Әрбір 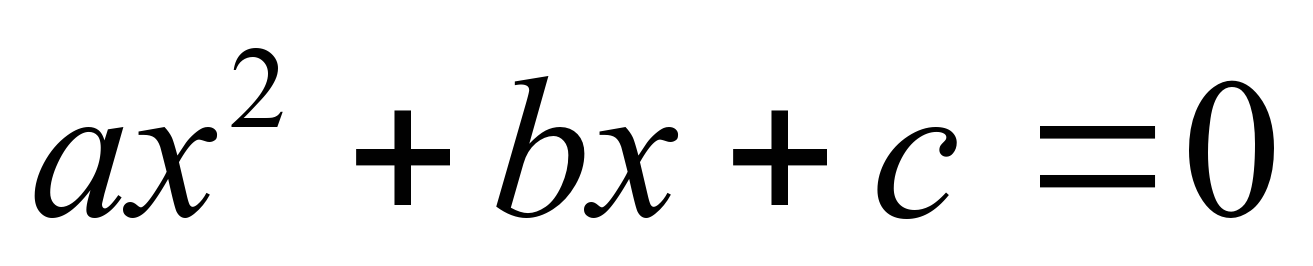теңдеуі үшін 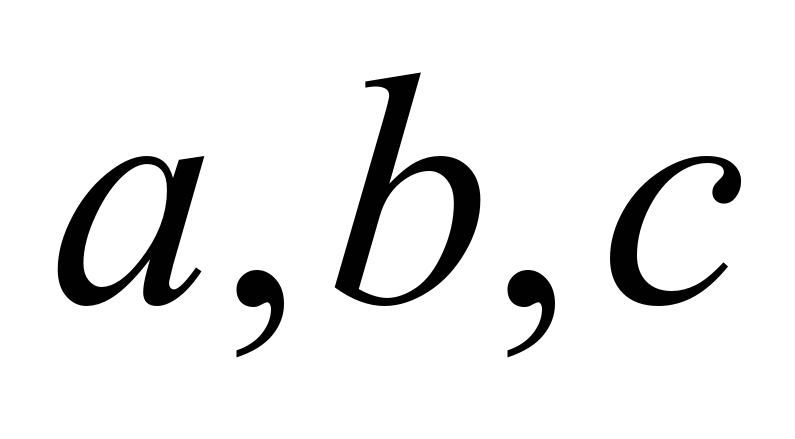мәндерін ата

а) 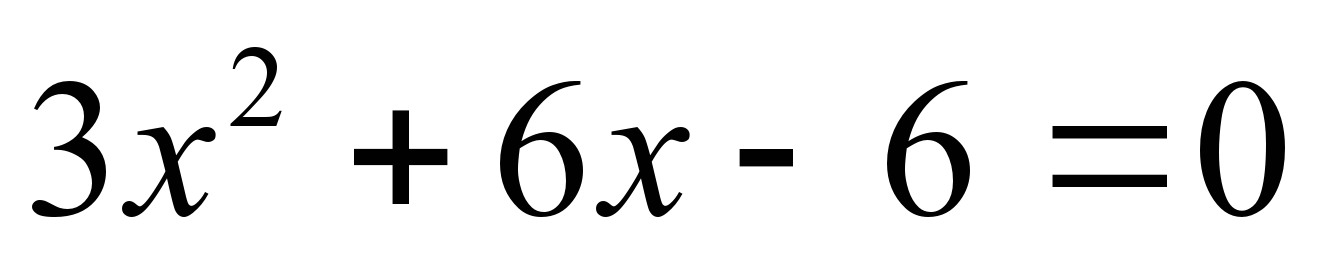б)

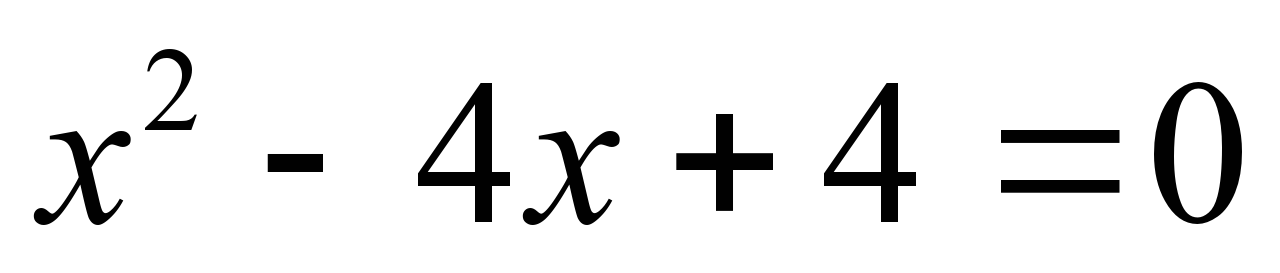№2 . 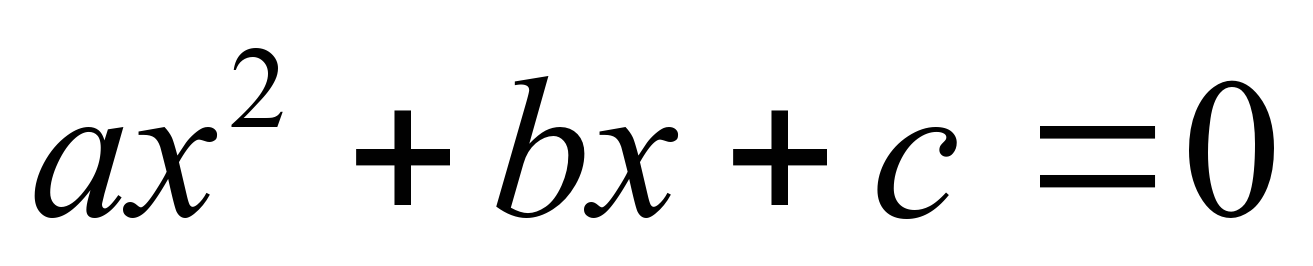квадрат теңдеуінің дискриминантын 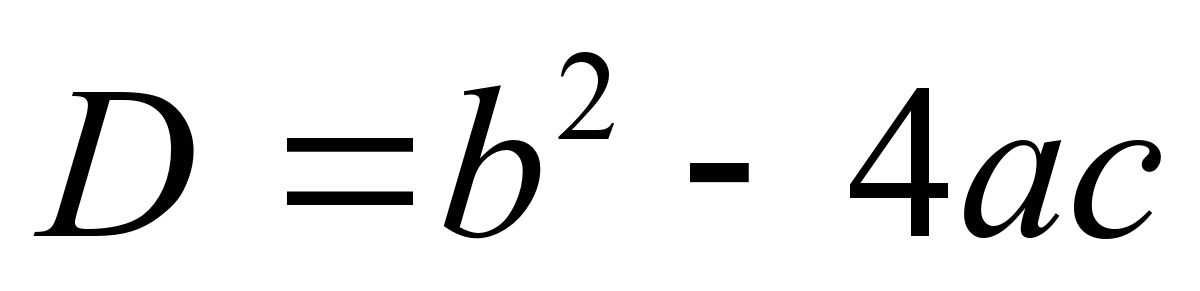формуласын есептеуді жалғастыр.

5х² - 7х + 2 = 0, D = b² - 4ac = (-7)² – 4· 5 · 2 = …;

№3. Теңдеуді шешуді аяқта. 3х² - 5х – 2 = 0.

D = b² - 4ac = (-5)²- 4· 3·(-2) = 49; х₁= … х₂=…

В деңгей .Теңдеуді шеш: а) 6х²– 4х + 32 = 0; б) х² + 5х - 6 = 0.

С деңгей

Теңдеуді шеш: а) -5х²– 4х + 28 = 0; б) 2х²–8х–2=0. x₁=2+, x₂=2–

Қосымша тапсырма. а –ның қандай мәнінде х² - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?

2 нұсқа.

А деңгей №1. Әрбір ax² + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.

а) 4х² - 8х + 6 = 0, б) х² + 2х - 4 = 0

№2. №2 . 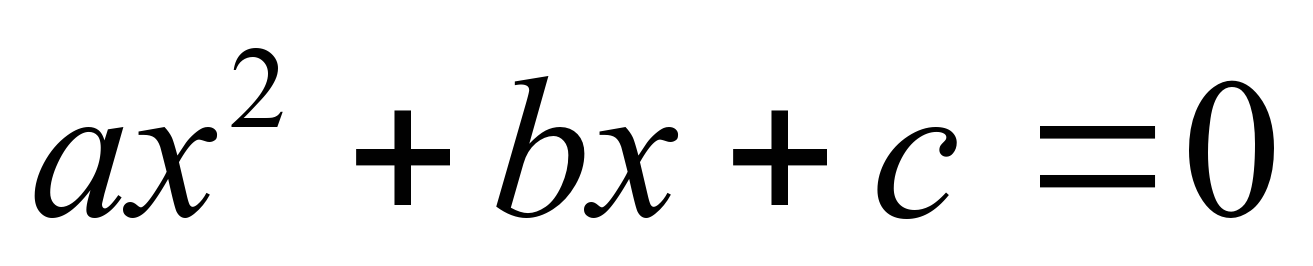квадрат теңдеуінің дискриминантын 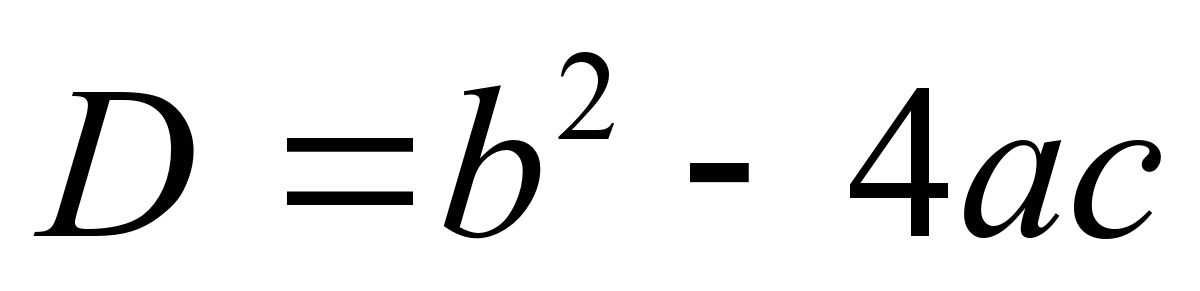формуласын есептеуді жалғастыр.

5х² + 8х - 4 = 0, D = b² - 4ac = 8² – 4· 5 · (- 4) = …;

№3. Теңдеуді шешуді аяқта х² - 6х + 5 = 0.

D = b² - 4ac = (-6 )² - 4· 1·5 = 16; х₁= … х₂=…

В деңгей

Теңдеуді шеш : а) 3х²– 2х + 16 = 0; б) 3х² - 5х + 2 = 0.

С деңгей

Теңдеуді шешіңдер: а) 5х²+ 4х - 28 = 0; б) х²– 6х + 7 = 0; x₁=3+, x₂=3–.

Қосымша тапсырма. а –ның қандай мәнінде х² + 3ах + а = 0 теңдеуінің бір түбірі бар болады?

№1 . Әрбір 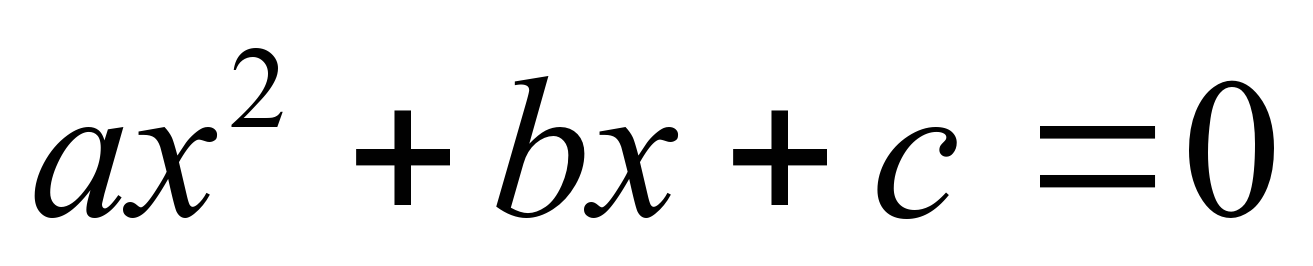теңдеуі үшін 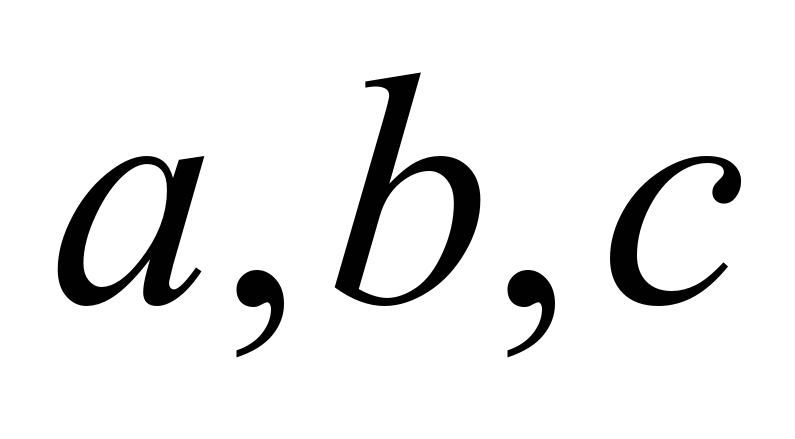мәндерін ата

а) 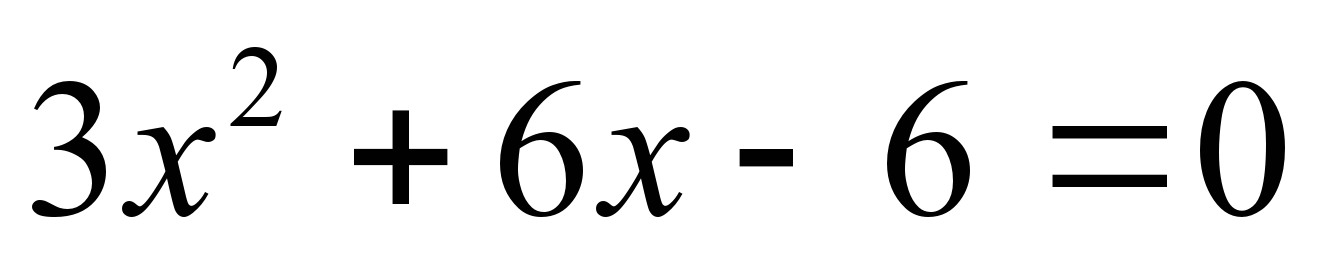б)

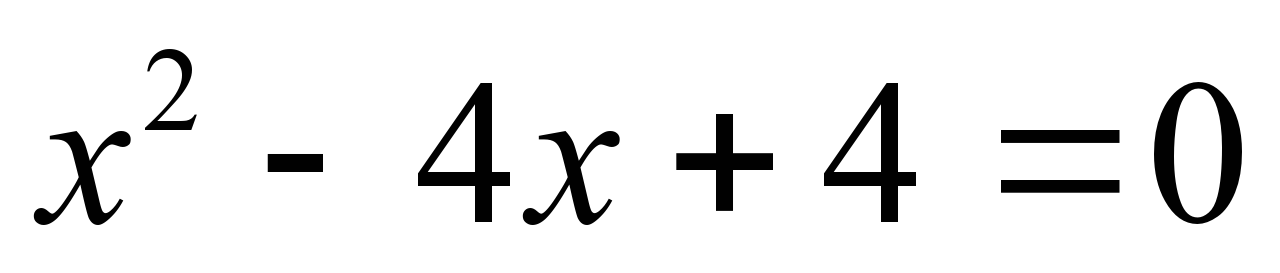№2 . 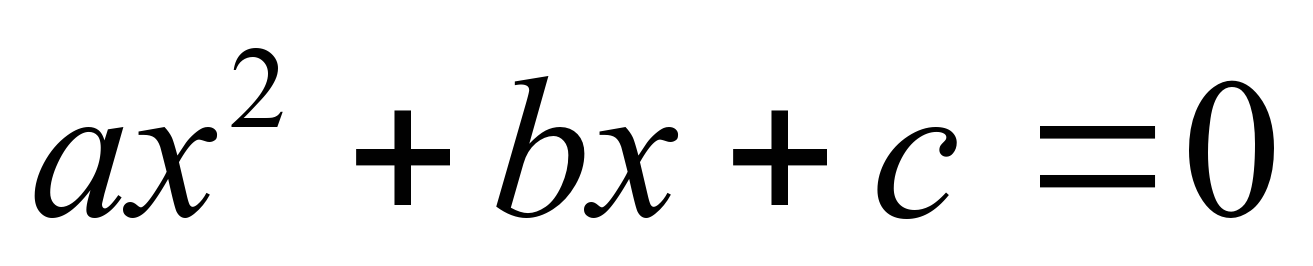квадрат теңдеуінің дискриминантын 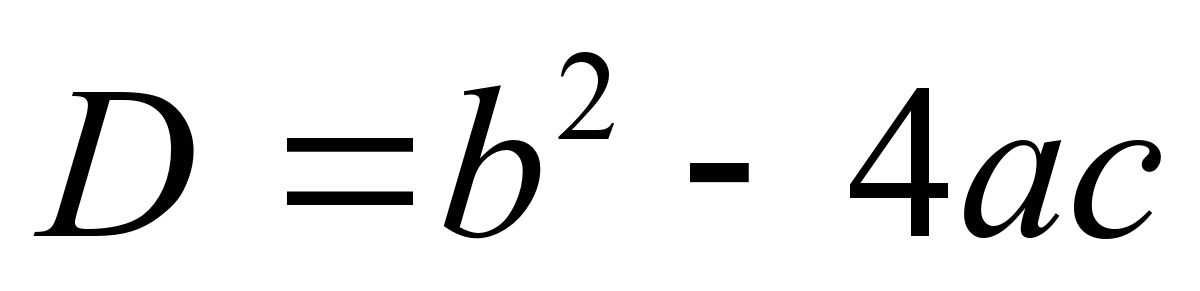формуласын есептеуді жалғастыр.

5х² - 7х + 2 = 0, D = b² - 4ac = (-7)² – 4· 5 · 2 = …;

№3. Теңдеуді шешуді аяқта. 3х² - 5х – 2 = 0.

D = b² - 4ac = (-5)²- 4· 3·(-2) = 49; х₁= … х₂=…

В деңгей .Теңдеуді шеш: а) 6х²– 4х + 32 = 0; б) х² + 5х - 6 = 0.

С деңгей

Теңдеуді шеш: а) -5х²– 4х + 28 = 0; б) 2х²–8х–2=0. x₁=2+, x₂=2–

Қосымша тапсырма. а –ның қандай мәнінде х² - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?

2 нұсқа.

А деңгей №1. Әрбір ax² + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.

а) 4х² - 8х + 6 = 0, б) х² + 2х - 4 = 0

№2. №2 . 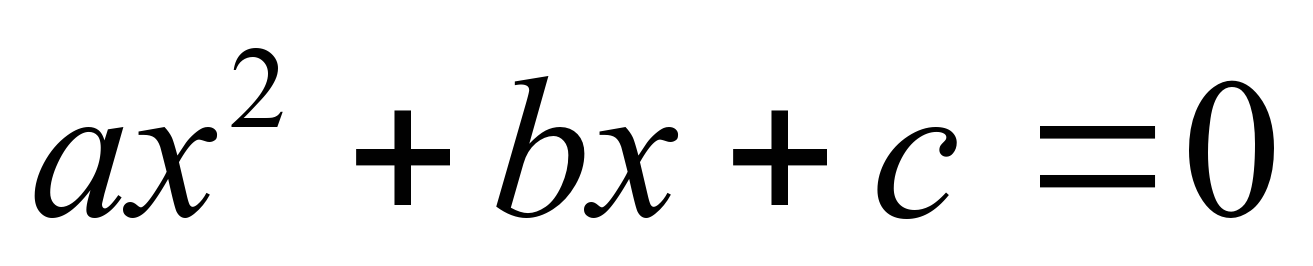квадрат теңдеуінің дискриминантын 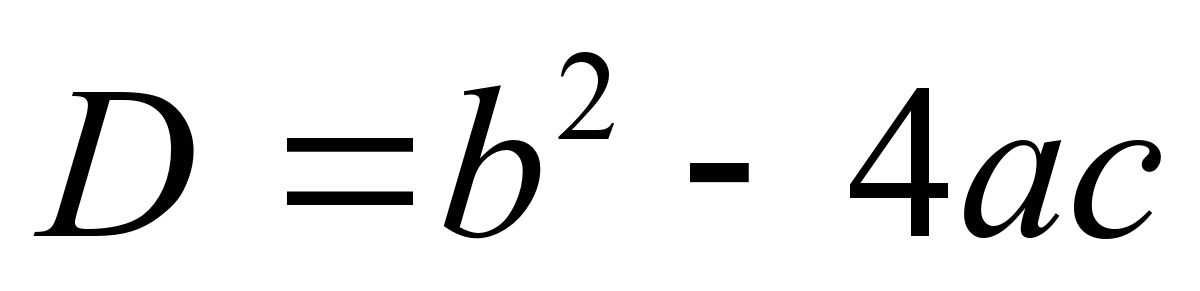формуласын есептеуді жалғастыр.

5х² + 8х - 4 = 0, D = b² - 4ac = 8² – 4· 5 · (- 4) = …;

№3. Теңдеуді шешуді аяқта х² - 6х + 5 = 0.

D = b² - 4ac = (-6 )² - 4· 1·5 = 16; х₁= … х₂=…

В деңгей

Теңдеуді шеш : а) 3х²– 2х + 16 = 0; б) 3х² - 5х + 2 = 0.

С деңгей

Теңдеуді шешіңдер: а) 5х²+ 4х - 28 = 0; б) х²– 6х + 7 = 0; x₁=3+, x₂=3–.

Қосымша тапсырма. а –ның қандай мәнінде х² + 3ах + а = 0 теңдеуінің бір түбірі бар болады?

Аты жөні	сергіту	Тест	Теориядан сұрақ	Теңдеу шешу	Өзіндік жұмыс	Қорытынды
Ұпай саны

1 .Ауызша жұмыс. Әрбір дұрыс жауапқа 1 ұпай қояды.

Екінші дәрежелі теңдеу қалай аталады?
Квадрат теңдеудің түбірі неге байланысты?
ХХІ ғасыр қашан басталды?
D 0- ден үлкен болса,теңдеудің неше түбірі бар?
Айнымалысы бар теңдік
Білімді бағалайтын нашар баға?
Теңдеу шешу дегеніміз не?
Шаманың жоқтығын көрсететін цифр.
Бірінші коэффициенті 1 болатын квадрат теңдеу.
1 жылда күн неше рет шығады?
Дискриминанат 0-ден кіші болса, квадрат теңдеудің неше түбірі бар.

2. Тест «Квадрат теңдеудің түрлері»