Математический аппарат, используемый при изучении темы «Электромагнитные колебания»

Гармонические колебания и их характеристики
- Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания широко распространены в окружающем мире и могут иметь самую различную природу. Это могут быть механические (маятник), электромагнитные (колебательный контур) и другие виды колебаний. Особую роль в колебательных процессах имеет простейший вид колебаний - гармонические колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса .
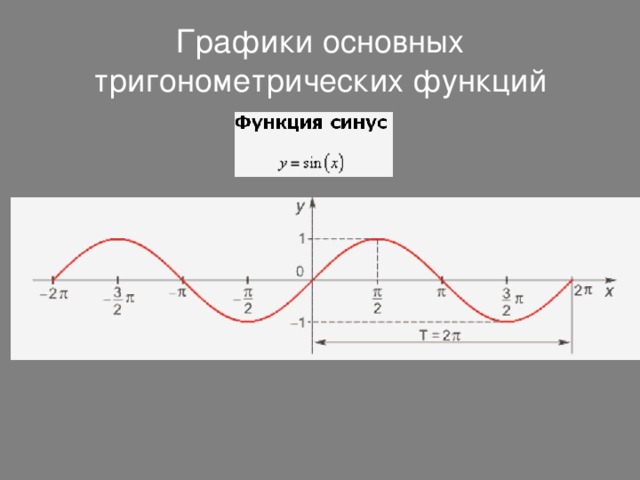
Графики основных тригонометрических функций
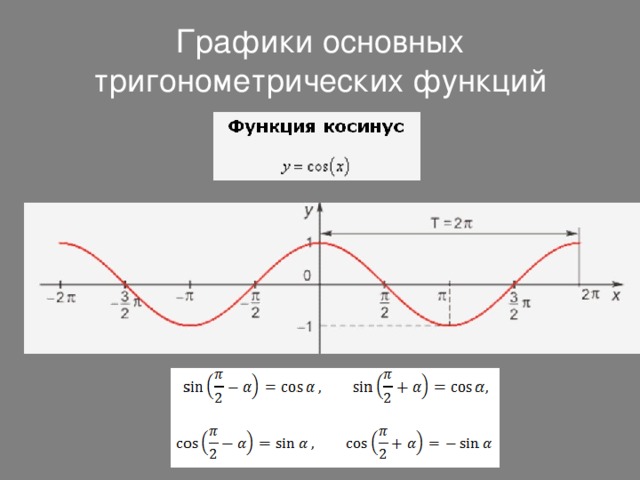
Графики основных тригонометрических функций
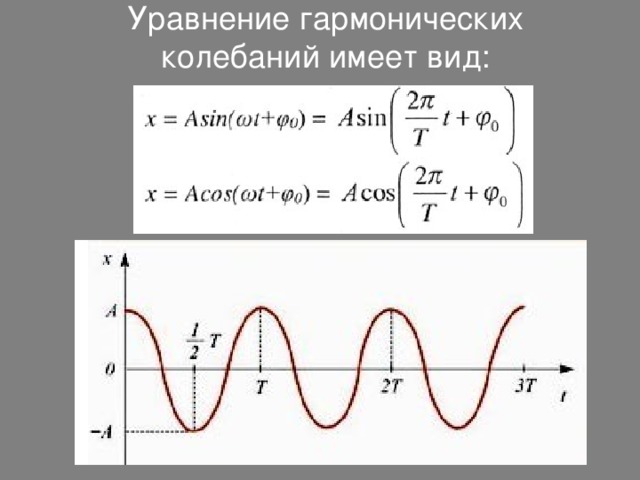
Уравнение гармонических колебаний имеет вид:
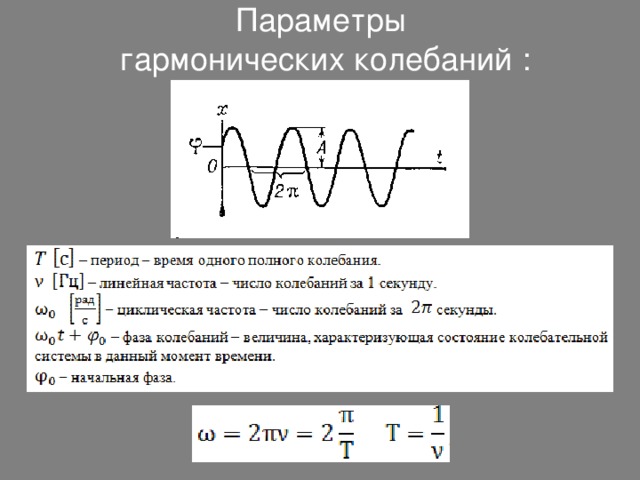
Параметры гармонических колебаний :


ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В . Магнитный поток Ф , пронизывающий рамку с площадью S равен:
Ф = BScos α = BScosωt ,
где α - угол между нормалью к рамке и вектором магнитной индукции .
По закону электромагнитной индукции Фарадея ЭДС индукции равна скорости изменения магнитного потока, и противодействует этому изменению:
ε = −∆ Ф /∆ t

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции :
ε = −∆ Ф /∆t = BSωsinωt = ε m sin ωt
где – ε m = BSω - амплитудное значение ЭДС индукции.
Если к контуру подключить источник внешней гармонической ЭДС ε = ε m sinωt , то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ , совпадающей с частотой источника. При этом вынужденные колебания совершают заряд q , разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери.

Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. В промышленных цепях переменного тока России принята частота 50 Гц.
I m , Q m , U m - амплитуды силы тока, заряда, напряжения i, q, u - мгновенные значения силы тока, заряда, напряжения

Для подсчета количества теплоты
Q = IUt ,
выделяющегося при прохождении переменного тока по проводнику с активным сопротивлением R, используют действующие значения тока и напряжения:

I тур
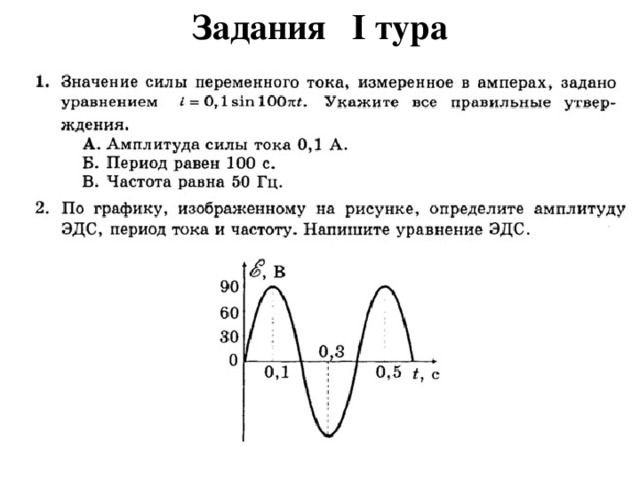
Задания I тура

I тур
1 команда
2 команда
3 команда
1б
1б
1б
1б
2б
Т=0,4с,
ν = 2 ,5Гц
Т=0, 0 4с,
ν = 2 5Гц
w = 5π рад/с
Т=0, 02 с,
ν = 5 0 Гц
1б
1б
1б
1б
2б
w = 50π рад/с
e = 90 sin 5 π t В
w = 100π рад/с
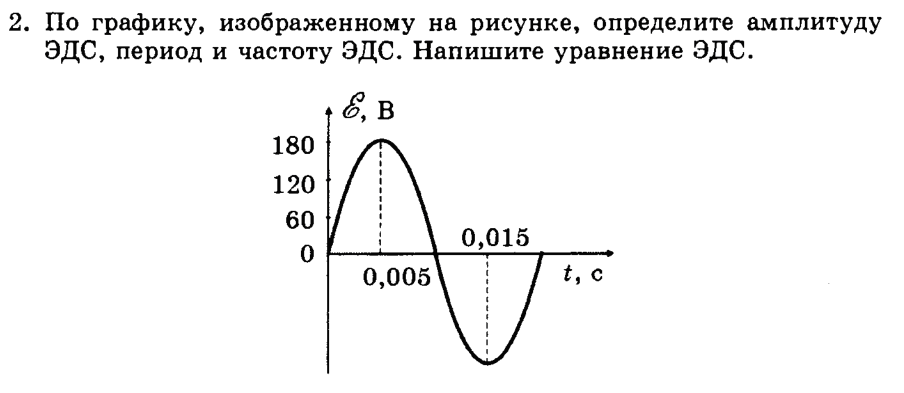
2 . Em =180 В,
Т=0, 02 с,
ν = 5 0 Гц
i = 12 sin 50 π t В
U = 90 sin 100 π t В
w = 100π рад/с
e = 180 sin 100 π t В

Резистор, конденсатор и катушка в цепи переменного тока

Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим активным сопротивлением R . Сопротивление R называется активным, потому что при наличии нагрузки обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников – они нагреваются.
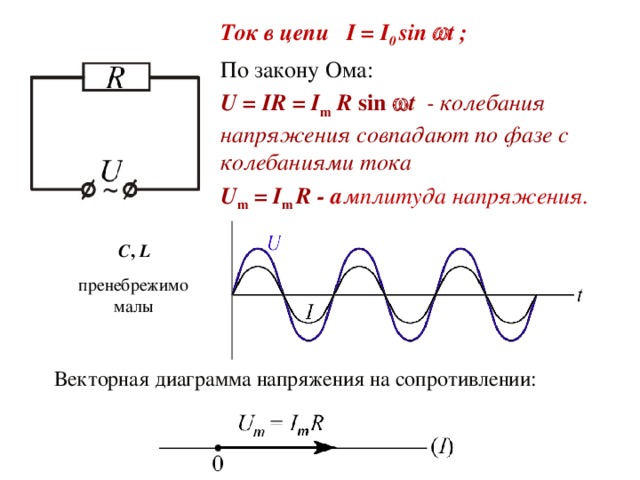
Ток в цепи I = I 0 sin t ;
По закону Ома:
U = IR = I m R sin t - колебания напряжения совпадают по фазе с колебаниями тока
U m = I m R - а мплитуда напряжения.
С , L
пренебрежимо малы
Векторная диаграмма напряжения на сопротивлении:

Конденсатор в цепи переменного тока
Как переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Дело в том, что происходит периодическая зарядка и разрядка конденсатора по действием переменного напряжения. Ток идущий в цепи при перезарядке конденсатора, нагревает нить накала лампы
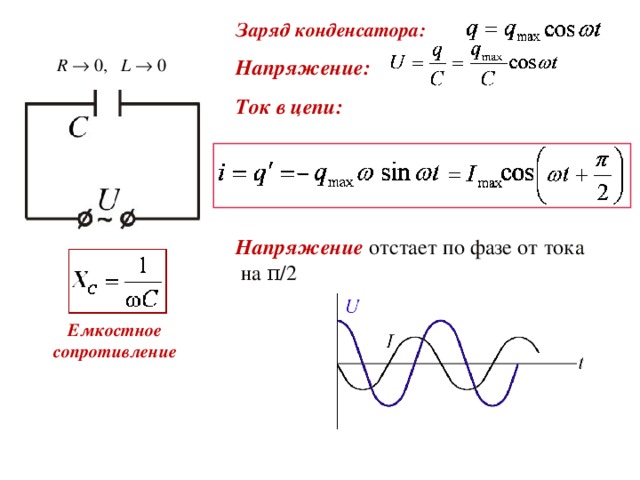
Заряд конденсатора:
Напряжение:
Ток в цепи:
Напряжение отстает по фазе от тока на π /2
R 0 , L 0
Емкостное сопротивление

Индуктивность в цепи переменного тока
Катушка индуктивности оказывает сопротивление проходящему по ней переменному току. ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и, наоборот, поддерживает его при убывании. Сопротивление вызывается в конечном счете индуктивностью катушки и называется оно индуктивным сопротивлением.
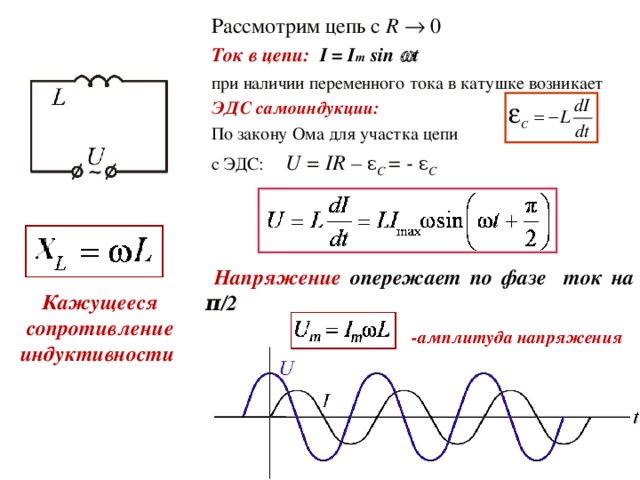
Рассмотрим цепь с R 0
Ток в цепи: I = I m sin t
при наличии переменного тока в катушке возникает ЭДС самоиндукции:
По закону Ома для участка цепи
с ЭДС: U = IR – ε C = - ε C
Напряжение опережает по фазе ток на π /2
-амплитуда напряжения
Кажущееся сопротивление индуктивности

Кафедра физики
Колебательный контур
Среди различных колебательных систем особое место занимают электромагнитные (электрические) системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур .
Колебательный контур – это электрическая цепь, состоящая из последовательно включенных резистора сопротивлением R . катушки индуктивностью L , и конденсатора емкостью C .

Идеальный колебательный контур

Идеальный колебательный контур
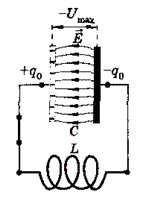
Идеальный колебательный контур состоит из конденсатора и катушки индуктивности. Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам
заряды .
В момент времени между обкладками конденсатора возникает электрическое поле, энергия которого равна:
Вся энергия колебательного контура сосредоточена в конденсаторе. Если теперь замкнуть конденсатор на катушку индуктивности, то в контуре потечет возрастающий со временем ток I . Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума.Вся энергия колебательного контура будет сосредоточена в магнитном поле катушки и равна: .
Кафедра физики
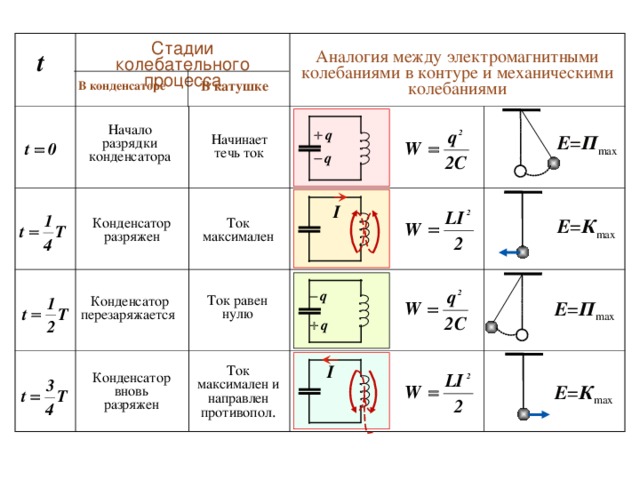
Стадии колебательного процесса
Аналогия между электромагнитными колебаниями в контуре и механическими колебаниями
В катушке
В конденсаторе
Начало разрядки конденсатора
Е = П max
Начинает течь ток
Конденсатор разряжен
Ток максимален
Е = К max
Ток равен нулю
Конденсатор перезаряжается
Е = П max
Ток максимален и направлен противопол .
Конденсатор вновь разряжен
Е = К max
26
26

Таким образом, полная энергия колебательного контура в любой момент времени равна сумме энергий магнитного и электрического полей
Колебания, при которых происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки, называются ЭЛЕКТРОМАГНИТНЫМИ колебаниями.

Уравнение свободных колебаний для заряда
q = q(t) конденсатора в контуре имеет вид:
А уравнение колебаний силы тока равно первой производной заряда по времени:
,где
Уравнение гармонических колебаний напряжения на конденсаторе:
В этих формулах: q m - амплитуда заряда, I m - амплитуда тока, U m – амплитуда напряжения.
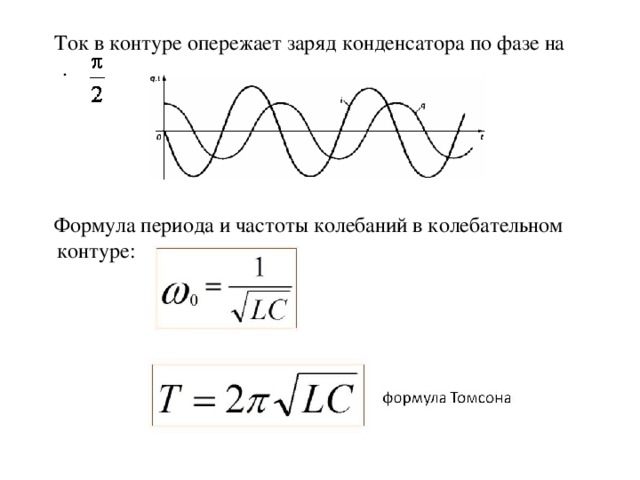
Ток в контуре опережает заряд конденсатора по фазе на .
Формула периода и частоты колебаний в колебательном контуре:

Энергия электрического поля конденсатора
Энергия магнитного поля катушки
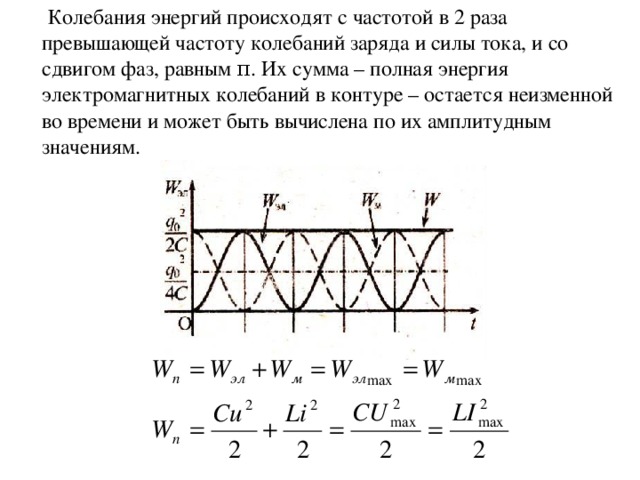
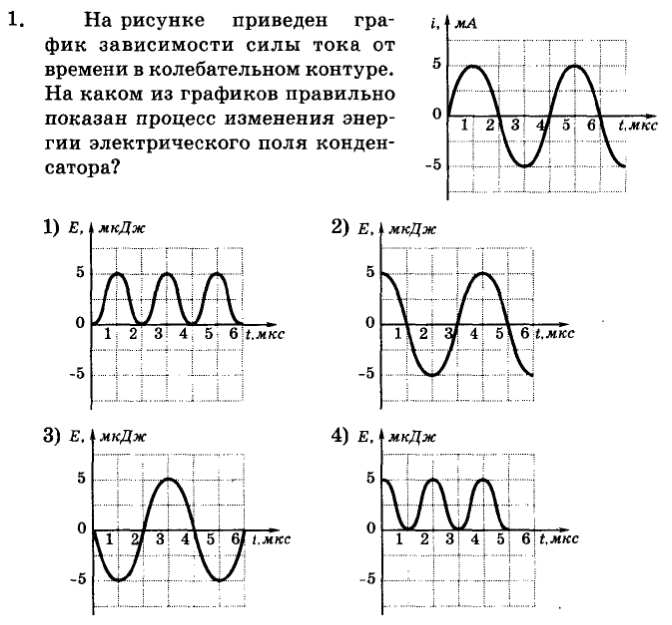
Колебания энергий происходят с частотой в 2 раза превышающей частоту колебаний заряда и силы тока, и со сдвигом фаз, равным π . Их сумма – полная энергия электромагнитных колебаний в контуре – остается неизменной во времени и может быть вычислена по их амплитудным значениям.

II тур
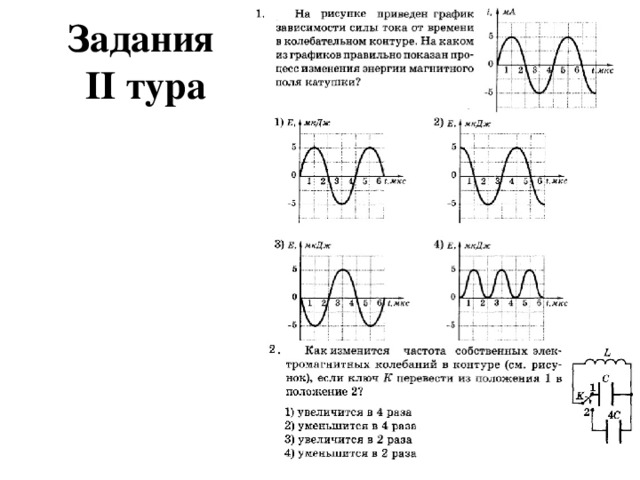
Задания II тура

Ответы II тура
1 команда
3 команда
2 команда
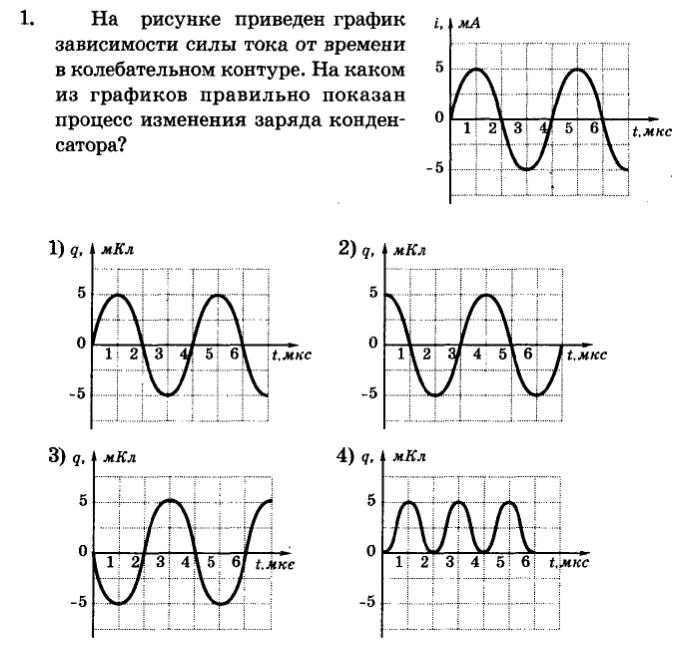
1.4
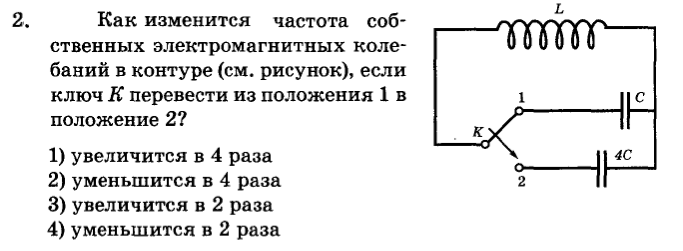
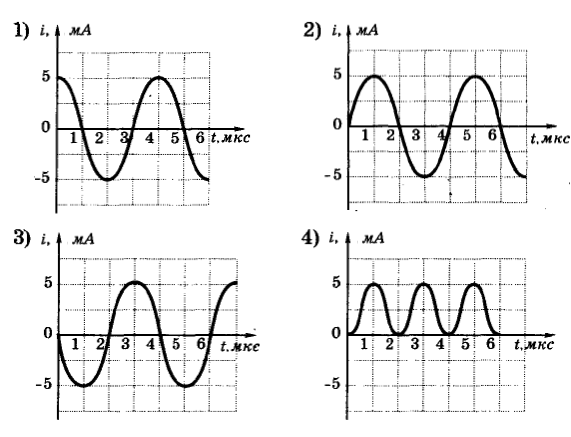
2.4
4 команда

III тур

Задание III тура Заряд на обкладках конденсатора колебательного контура изменяется по закону q = 3·10 –7 cos800πt . Индуктивность контура 2Гн . Пренебрегая активным сопротивлением, заполните бланк ответа.
Уравнение гармонических колебаний заряда конденсатора
Амплитуда колебаний заряда
Индуктивность катушки
Циклическая частота колебаний
Электроемкость конденсатора
Уравнение гармонических колебаний тока в контуре
Амплитуда тока
Максимальное значение энергии электрического поля конденсатора
Максимальное значение магнитного поля катушки индуктивности
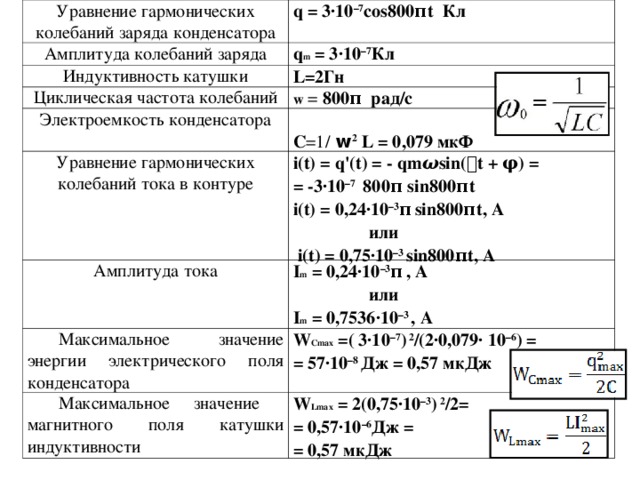
Уравнение гармонических колебаний заряда конденсатора
q = 3·10 –7 cos800πt Кл
Амплитуда колебаний заряда
q m = 3·10 –7 Кл
Индуктивность катушки
L=2 Гн
Циклическая частота колебаний
w = 800π рад/с
Электроемкость конденсатора
Уравнение гармонических колебаний тока в контуре
C =1 / w 2 L = 0 ,0 7 9 мкФ
i(t) = q'(t) = - qm 𝝎 sin( 𝝎 t + φ) =
= -3·10 –7 800 π sin800 π t
i(t) = 0,24·10 –3 π sin800 π t , А
или
i(t) = 0,75·10 –3 sin800 π t , А
Амплитуда тока
I m = 0,24·10 –3 π , А
или
I m = 0,75 36 ·10 –3 , А
Максимальное значение энергии электрического поля конденсатора
Максимальное значение магнитного поля катушки индуктивности
W Cmax =( 3·10 –7 ) 2 /(2·0,079· 10 –6 ) =
= 57·10 –8 Дж = 0,57 мкДж
W Lmax = 2(0,75·10 –3 ) 2 /2=
= 0,57·10 –6 Дж =
= 0,57 мкДж

Список используемых ресурсов
- http://www.yaklass.ru/materiali?mode=lsntheme&themeid=132
- http://school-box.ru/fizika/prezentazii/989-prezentaziya-po-fizike-elektromagnitnie-kolebaniya.html
- http://www.docme.ru/doc/23255/lekcii-18--19-kolebatel._nyj-kontur-4--11-maya
- Решу ЕГЭ Дмитрия Гущина
- Физика. 11кл. Разноур. самост. и контр. работы_Кирик Л.А_2009 -192с

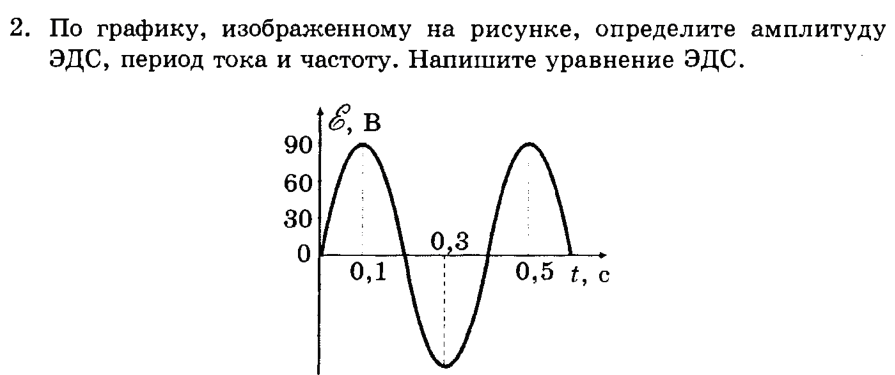

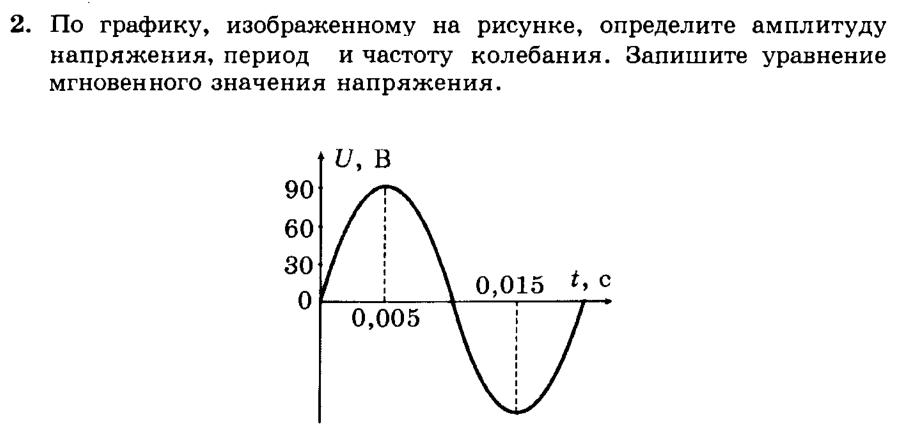









 II
II





















































