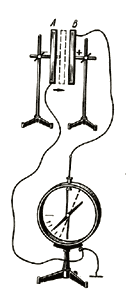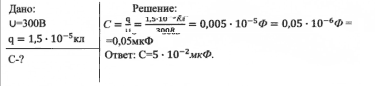Тема урока: Электроемкость. Единицы электроемкости. Конденсаторы. 10 класс

Атырауская область, Курмангазинский район, с. Ганюшкино, сш имени М.В. Ломоносова, Нурлан Сабыров

Тема урока: Электроемкость. Единицы электроемкости. Конденсаторы. 10 класс

Образовательные цели:  сформировать понятия электрической ёмкости, единицы ёмкости; изучить зависимость ёмкости от размеров проводника, диэлектрической проницаемости среды и расстояния между пластинами конденсатора.

• Воспитательные цели:  продолжить формирование представления о строении вещества; о частицах, входящих в состав молекул и атомов; показать реальность электрического поля.

• Развивающие цели:  формировать умения сравнивать результаты опытов, формулы, а также величины характеризующие электроёмкость; научиться использовать знания формул в решении задач.

Оборудование: 2 электрометра, металлические пластины на изолирующих подставках, электростатическая машина, соединительные провода, конденсаторы переменной и постоянной ёмкости.

Демонстрации:

• Зависимость электроёмкости от расстояния между пластинами.

• Зависимость ёмкости плоского конденсатора от площади пластины.

• Зависимость электроёмкости от диэлектрической проницаемости среды.

План урока.

1. Проверка ранее изученного материала.

2. Изучение нового материала.

1. Понятие о конденсаторе.

2. Электроёмкость конденсатора.

3. Единица электроёмкости

4. Формула электроёмкости плоского конденсатора.

5. Виды конденсаторов.

1. Закрепление. Решение задач. Беседа по вопросам.

2. Итог урока.

Стадия вызова:

Ход урока:

1. Проверка раннего изученного материала (устно) 

• В каких единицах измеряется напряжённость электрического поля?

• В каких единицах измеряется электрический заряд?

• Записать формулу закона Кулона для вакуума в СИ.

• Записать формулу закона Кулона для среды в СИ.

• Что такое электрическое поле?

• Как называют поле неподвижных зарядов?

• Записать формулу напряженности.

• Чему равна напряжённость поля точечного заряда?

• Чему равна разность потенциалов между двумя точками заряженного проводника?

• Стадия осмысления:

Изучение нового материала.

Слово ''конденсатор'' происходит от латинского слова condensare, что означает ''сгущение''. В учении об электрических явлениях этим словом обозначают устройства, позволяющие сгущать электрические заряды и связанное с этими зарядами электрическое поле.

Простейший конденсатор состоит из двух проводников, разделённых диэлектриком, толщина которого мала по сравнению с размерами проводника.

Свойство конденсатора сгущать электрические заряды и связанное с ним электрическое поле можно наблюдать на опыте.

Опыт 1. Две металлические пластины, укреплённые на изолирующих подставках, располагаем параллельно друг другу и присоединяем к электрометру. Одну из пластин соединяем с землёй.

(рис.1)

Одной из пластин сообщаем положительный заряд q. Другая при этом получит через влияние отрицательный заряд- q. Электрометр покажет разность потенциалов между пластинами.

Сообщим первой пластине дополнительно заряд q тем же способом, прикоснувшись наэлектризованным шаром. Теперь на пластинах находятся заряды 2 q и -2 q. Показания электрометра при этом увеличились в двое.

Не меняя зарядов, начнём сближать пластины. Напряжение между пластинами будет уменьшаться. При некотором расстоянии оно станет таким, каким оно было при зарядах q и –q. Прекратим сближение пластин и вновь первой пластине передадим дополнительный заряд q. Показания электрометра вновь увеличатся. При дальнейшем сближении пластин, замечаем, что при некотором, ещё меньшем расстоянии между ними электрометр вновь покажет прежнюю разность потенциалов. Следовательно, сдвигая пластины конденсатора, можно при одном и том же напряжении накапливать на одной пластине положительные заряды q, 2q, 3q,…, а на другой- равные по модулю отрицательные заряды. т.о, конденсатор накапливает заряды: поверхностная плотность зарядов увеличивается по мере сближения пластин.

Свойство конденсатора накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется особой величиной, называемой электроёмкостью.

Чтобы выяснить смысл этой величины, обратимся к исследованиям.

Опыт 2. Касаясь одинаково заряженными шарами внешней стороны пластины конденсатора, передаём этой пластине последовательно по заряду q. При этом заметим, что по мере увеличения заряда растёт напряжение между пластинами. Причём при зарядах q, 2q, 3q,… напряжение принимает значение U, 2U, 3U,…, возрастая пропорционально заряду. (рис.2) Но отношение заряда к напряжению остаётся постоянным: 

рис.2

Проведём такие же опыты с конденсатором, пластины которого имеют большую площадь; при этом расстояние между пластинами сделаем таким же. Увеличивая заряд одной из пластин на q, т.е. делая его равным 2q, 3q,…, заметим, что напряжение между пластинами принимает значения U₁, U₂, 3U₁…, где U₁ U. Но .

Для того чтобы второй конденсатор зарядить до такого же напряжения, как и первый, ему надо сообщить больший заряд. Второй конденсатор обладает большей электрической ёмкостью, т.е. второму конденсатору соответствует большее значение отношения заряда к напряжению. Следовательно, величина С характеризует электрическую ёмкость конденсатора.

Электрической ёмкостью конденсатора называется скалярная величина, характеризующая его свойство накапливать и сохранять электрические заряды и связанное с этими зарядами электрическое поле. Электроёмкость конденсатора равна отношению заряда одной из пластин к напряжению между ними: 

За единицу электроёмкости в СИ принимается электроёмкость конденсатора, напряжение между обкладками конденсатора которого равно 1В, когда на его обкладках имеются разноимённые заряды по 1Кл. Эта единица названа фарад в честь М.Фарадея:  . На практике применяются:      

Из рассмотренных исследований делаем вывод, что С конденсатора зависит от площади S пластин и расстояния d между ними:  .

Опыт 3. Кроме того, электрическая ёмкость конденсатора зависит от рода диэлектрика, находящегося между пластинами. Внесём в пространство между пластинами заряженного конденсатора лист какого-либо диэлектрика. Мы видим, что напряжение между пластинами уменьшилось.(рис. 3,4) Значит, электрическая ёмкость конденсатора увеличилась 

Выведем формулу для расчёта электроёмкости плоского конденсатора. По определению  . Учитывая, что U = Ed, а , получаем:

Полученная формула согласуется с результатами рассмотренных опытов.

Выслушаем два заранее подготовленных сообщения учащихся о различных типах конденсаторов (о конденсаторах переменной ёмкости, технических бумажных и электролитических конденсаторах), их сравнительной характеристике, устройстве и применении.

1.Сообщение.

В зависимости от назначения конденсаторы имеют различное устройство. Технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Алюминиевая фольга и бумажные ленты туго свёрнуты в пакет небольшого размера. Бумажный конденсатор, имея размеры спичечного коробка, обладает электроёмкостью до 10 мкФ (металлический шар такой же ёмкости имел бы радиус 90 км).

В радиотехнике широко применяют конденсаторы переменной электроёмкости. Такой конденсатор состоит из двух систем металлических пластин, которые при вращении рукоятки могут входить одна в другую. При этом меняется площадь перекрывающейся части пластин и, следовательно, их электроёмкость. Диэлектриком в таких конденсаторах служит воздух.

2.Сообщение.

Значительного увеличения электроёмкости за счёт уменьшения расстояния между обкладками достигают в так называемых электролитических конденсаторах. Диэлектриком в них служит очень тонкая плёнка оксидов, покрывающих одну из обкладок. Второй обкладкой служит бумага, пропитанная раствором специального вещества (электролита). При включении электролитических конденсаторов надо обязательно соблюдать полярность.

В слюдяных конденсаторах в качестве диэлектрика используют слюду, а обкладками служит металлическая фольга или тонкий слой металла, нанесённый непосредственно на слюду. Слюдяные конденсаторы устанавливают, главным образом, в электрических цепях высокой частоты.

В радиотехнике широкое распространение получили керамические конденсаторы, имеющие небольшие размеры, но обладающие хорошими электрическими свойствами. Конструктивно их выполняют в виде трубок или дисков из керамики, а обкладками служит слой металла, нанесённый на керамику.

рефлексия

1. Закрепление изученного материала.

1. Решение задач с помощью учителя.

• Какова электроёмкость (в микрофарадах) конденсатора, если при напряжении на его обкладках 300В заряд равен1,5 *10^-5кл?

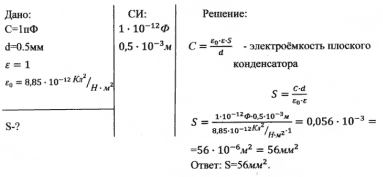
• Какую площадь должны иметь пластины плоского воздушного конденсатора для того, чтобы его электроёмкость была равна 1пФ? Расстояние между пластинами q =0,5мм.

• При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 50 В. Какова диэлектрическая проницаемость диэлектрика?

• Площадь каждой пластины плоского конденсатора равна 520 см². На каком расстоянии друг от друга надо расположить пластины в воздухе, чтобы емкость конденсатора была равна 46 пФ?

• Плоский конденсатор состоит из двух пластин площадью 50 см² каждая. Между пластинами находится слой стекла. Какой наибольший заряд можно накопить на этом конденсаторе, если при напряженности поля 10 МВ/м в стекле происходить пробой конденсатора?

1. Беседа по вопросам.

• Что называют ёмкостью двух проводников? (электроёмкостью двух проводников называют физическую величину, характеризующую свойство проводников накапливать электрические заряды; она равна отношению заряда одного из проводников к напряжению между проводниками.)

• Назовите единицы ёмкости. (Ф, мкФ, пФ.)

• Какая система проводников называется конденсатором?(Конденсатор- эта система двух или более обкладок, разделённых диэлектриком. Заряженный конденсатор содержит на пластинах (обкладках) равные по величине, но противоположные по закону заряды.)

• Как зависит электроёмкость плоского конденсатора от его геометрических размеров? (Ёмкость тем больше, чем больше площадь обкладок и чем меньше расстояние между ними.)

1. Итог урока.

Учитель: Что нового узнали сегодня на уроке?

Ученик: Узнали, что такое электроёмкость и от чего она зависит; что такое конденсатор, какие бывают конденсаторы; где применяются конденсаторы; научились решать задачи на расчёт электроёмкости плоского конденсатора.

Домашняя задания: п. 8.10, 8.11 Упр.18 (1.2.3)