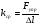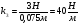Схема экспериментальной установки 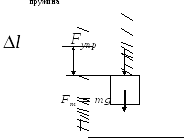 Расчетные формулы При равновесии системы тел (пружина – грузы) 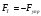 , , 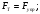 по IIIзакону Ньютона по IIIзакону Ньютона 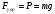 ; по закону Гука модуль силы упругости равен ; по закону Гука модуль силы упругости равен 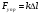 . . В итоге получаем формулу для расчета жесткости 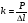 . . Среднее значение жесткости пружины можно определить по формуле 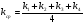 . . Результаты измерения веса грузов и удлинения пружины (составление таблицы) | N | m, кг | P, Н | Δl, м | k, 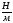 , , | kср, 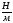 | | 1 | 0,102 | 1 | 0,025 | 40 |
40 | | 2 | 0,204 | 2 | 0,5 | 40 | | 3 | 0,306 | 3 | 0,75 | 40 | | 4 | 0,408 | 4 | 0,1 | 40 |
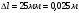 - измерение считается верным, если приведено в пределах от 23 мм до 27 мм, погрешность определяется главным образом погрешностью отсчета. - измерение считается верным, если приведено в пределах от 23 мм до 27 мм, погрешность определяется главным образом погрешностью отсчета.
4. График зависимости силы упругости от удлинения пружины 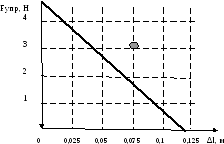 Среднее значение жесткости пружины можно так же найти, используя данный график, выбрав произвольную точку на графике и определив значения силы и удлинения. 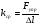 5. Установление закономерности связи между силой упругости и удлинением пружины При равномерном растяжении пружины – приложенная к пружине сила равна по модулю и противоположна по направлению силе упругости, возникающей при деформации пружины. Формулировка закона Гука: Модуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела. Запись формулы закона Гука: 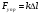 , где Δl – удлинение тела (изменение его длины), k -коэффициент пропорциональности, называемый жесткостью. , где Δl – удлинение тела (изменение его длины), k -коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости k . . Закон Гука хорошо выполняется только при упругих, малых деформациях. Построенный по результатам измерений график демонстрирует прямо пропорциональную зависимость между силой упругости, возникающей в пружине при деформации (растяжении), и удлинением пружины. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Таким образом, наблюдается закономерность между изменением величины силы упругости, возникающей в пружине при деформации, и удлинением пружины. Значит, подтверждается закон Гука для упругой, малой деформации 6. Численное значение жесткости пружины (пример расчета) 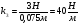 Внимание!!! (Указание экспертам): Оценка границ интервала, внутри которого может оказаться результат, полученный учеником, который необходимо признать верным, рассчитывается методом границ с учетом погрешности каждого из приборов (см. Характеристика оборудования).  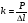 , то нижняя граница жесткости НГ , то нижняя граница жесткости НГ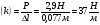 ; верхняя граница жесткости ВГ ; верхняя граница жесткости ВГ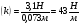 . . Таким образом, жесткость пружины по итогам измерений и вычислений  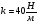 , значение измеряемой жесткости пружины может лежать в интервале , значение измеряемой жесткости пружины может лежать в интервале  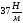
Погрешность измерений (Внимание!!! (Указание экспертам)): при хорошей математической подготовке учащихся и их знакомством с системой расчета погрешности) можно рассмотреть еще один вариант ее оценки): Если учесть  , то относительная погрешность вычисляется следующим образом: , то относительная погрешность вычисляется следующим образом:    , где , где  ; ;
 ; ;    . . Абсолютная погрешность измерения жесткости пружины  ; ;  . . Таким образом, жесткость пружины равна   | 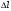 , см
, см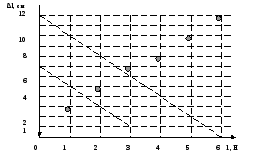
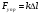 , где Δl – удлинение тела (изменение его длины), k -коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости k
, где Δl – удлинение тела (изменение его длины), k -коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости k .
.

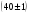 Н/м;
Н/м;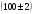 г;
г;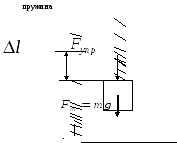
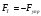 ,
, 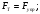 по IIIзакону Ньютона
по IIIзакону Ньютона 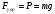 ; по закону Гука модуль силы упругости равен
; по закону Гука модуль силы упругости равен 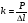 .
.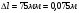 - измерение считается верным, если приведено в пределах от 73 мм до 77 мм, погрешность определяется главным образом погрешностью отсчета.
- измерение считается верным, если приведено в пределах от 73 мм до 77 мм, погрешность определяется главным образом погрешностью отсчета.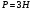
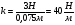

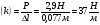 ; верхняя граница жесткости ВГ
; верхняя граница жесткости ВГ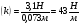 .
. 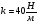 , значение измеряемой жесткости пружины может лежать в интервале
, значение измеряемой жесткости пружины может лежать в интервале 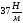

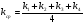 .
.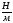 ,
,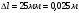 - измерение считается верным, если приведено в пределах от 23 мм до 27 мм, погрешность определяется главным образом погрешностью отсчета.
- измерение считается верным, если приведено в пределах от 23 мм до 27 мм, погрешность определяется главным образом погрешностью отсчета.