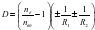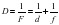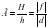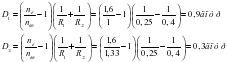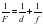Конспект урока по физике в 11 классе по теме: "Формула тонкой линзы. Увеличение линзы".

Тема: Формула тонкой линзы. Увеличение линзы.

Цель урока: Вывести формулу тонкой линзы и научиться решать задачи на применение этой формулы.

Ход урока:

1. Организационный момент.
2. Подготовка к восприятию материала (фронтальный опрос).

Вопросы:

• Какая линза называется тонкой?
• Какую линзу называют собирающей, рассеивающей?
• Какими лучами нужно пользоваться, чтобы получить изображение предмета в линзе?
• Каким получается изображение, если предмет расположен в двойном фокусе?
• Получим ли мы изображение, если предмет расположен в фокусе?
• Зависимость оптической силы линзы от радиусов кривизны поверхностей.

1. Формула тонкой линзы

1. Линейное увеличение линзы

1. Решение задач.

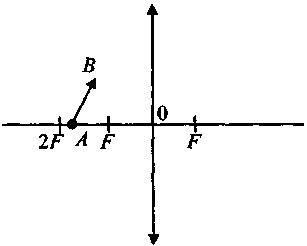
1. Постройте изображение данного предмета в линзе. Какое это изображение?
2. Определить оптическую силу стеклянной линзы (n = 1,6), находя­щейся в воздухе и в воде (n = 1,33), если линза:
   1. двояковыпуклая с радиусом кривиз­ны поверхностей R1 = 50 см; R2 = 30 см;
   2. выпукло-вогнутая с ра­диусом кривизны поверхностей R1 = 25 см; R2 = 40 см.

Дано

n1 = 1

n2 = 1,6

n3 = 1,33

R1 = 0,5 м;

R2 = 0,3 м;

Решение

Ответ: D1 = 3,2 дптр, D2 = 1,1 дптр.

D1, D2 – ?

Дано

n1 = 1

n2 = 1,6

n3 = 1,33

R1 = 0,25 м;

R2 = – 0,4 м;

Решение

,

Ответ: D1 = 0,9 дптр, D2 = 0,3 дптр.

D1, D2 – ?

1. При помощи линзы, фокусное расстояние которой 20 см, получено изображение предмета на экране, удаленном от линзы на 1 м. На каком расстоянии от линзы находится предмет? Каким будет изображение?

Дано

F = 0,2 м

f = 1 м;

Решение

Ответ: d = 0,25 м.

d – ?

1. Домашнее задание: §65

решить задачи.

1. Определить оптическую силу стеклянной линзы (n = 1,6), находящейся в воздухе и в сероуглероде (n = 1,65), если линза:
   1. двояковогнутая с радиусами кривизны R = 20 см; R2 = 40 см;
   2. плоско-выпуклая с радиусом кривизны выпуклой поверхно­сти R = 60 см;
   3. вогнуто-выпуклая с радиусами кривизны поверхностей R1 = 20 см; R2 = 35 см.
2. Свеча находится на расстоянии 12,5 см от собирающей лин­зы, оптическая сила которой равна 10 дптр. На каком расстоянии от линзы получится изображение и каким оно будет?