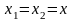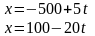| № п/п | Новые понятия | Содержание |
| 1 | Механика | изучает механическое движение |
| 2 | Кинематика
| раздел механики, который изучает описание движения тела, не рассматривая причин, вызвавших движение |
| 3 | Механическим движением тела | называется изменение его положения в пространстве относительно других тел с течением времени |
| 4 | Основная задача механики | определить положение тела в любой момент времени, т.е задать координаты x, y, z |
| 5 | Траектория | линия, которую описывает движущееся тело |
| 6 | Путь | длина траектории |
| 7 | Перемещение | вектор, соединяющий начальную и конечную точки траектории тела, описанной за некоторый интервал времени |
| 8 | Материальная точка | тело, размерами которого можно пренебречь в данных условиях движения: а) размеры тела значительно меньше, чем расстояния, которое оно проходит; б) тело движется поступательно |
| 9 | Поступательное движение | это движение, при котором все точки тела движутся одинаково |
| 10 | Тело отсчета | тело, относительно которого определяют положение другого тела |
| 11 | Система отсчета включает в себя | тело отсчета, связанную с ним систему координат и прибор для измерения времени |
| 12 | Прямолинейное равномерное движение (ПРД) | движение, при котором тело за любые равные промежутки времени осуществляет одинаковые перемещения |
| 13 | Скорость равномерного прямолинейного движения | векторная величина, равная отношению перемещения тела ко времени, за которое это перемещение совершено  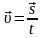
|
| 14 | Положение тела при ПРД определяем |  
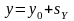  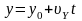 
|
| 15 | Под относительностью движения понимают | зависимость кинематических величин (координаты, скорости, пути, перемещения) от выбора системы отсчета 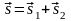 - закон сложения перемещений; - закон сложения перемещений; 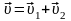 - закон сложения скоростей - закон сложения скоростей |
| 16 | Прямолинейное неравномерное движение | движение, при котором тело за одинаковые промежутки времени совершает различные перемещения |
| 17 | Средняя скорость при неравномерном движении
| равна отношению всего перемещения, совершенного телом, ко всему времени, за которое это перемещение совершено - величина векторная 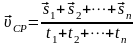 |
| 18 | Средняя путевая скорость | равна отношению всего пути, пройденного телом, ко всему времени, за которое этот путь пройден  |
| 19 | Мгновенная скорость | это скорость тела в данный момент времени или в данной точке траектории |
| 20 | Равноускоренное движение | Движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково. Ели при этом направление скорости не изменяется, то движение будет равноускоренным и прямолинейным |
| 21 | Ускорение | физическая величина, характеризующая быстроту изменения скорости к промежутку времени, за которое произошло это изменение 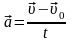 |
| 22 | Прямолинейное равноускоренное движение | характеризуется двумя векторными уравнениями:  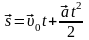
|
| 23 | Положение тела при равноускоренном прямолинейном движении | определяют по формулам: 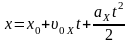 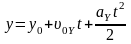 |
| 24 | Свободное падение | движение, происходящее только под действием силы притяжения Земли. Свободное падение описывается уравнениями равноускоренного движения 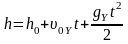 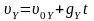 |
| 25 | Криволинейное движение | движение материальной точки по кривой (по окружности) |
| 26 | Равномерное движение по окружности | движение материальной точки по окружности с постоянной по модулю скоростью |
| 27 | При равномерном движении тела по окружности | его ускорение в любой точке траектории направлено по радиусу к центру окружности. Это ускорение называют центростремительным 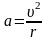 |
| 28 | Период | промежуток времени, за который тело совершает один полный оборот |
| 29 | Линейная скорость | 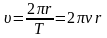
|
| 30 | Частота вращения | величина, равная числу оборотов, которое тело совершает за единицу времени, двигаясь по окружности  |
| 31 | Угловая скорость | величина, равная отношению угла поворота радиуса, проведенного из центра окружности к точке тела, ко времени, за которое совершен этот поворот 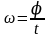 |
| 32 | Один радиан | это угол, соответствующей дуге, длина которой равна радиусу окружности |
| 33 | Связь между линейной и угловой скоростями | 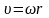
|
Выберите систему отчета: тело отчета, систему координат, прибор для измерения времени (положительное направление оси) или начертите предложенный в задаче график (или выполните вспомогательный рисунок).
Определите вид движения вдоль каждой оси координат и напишите кинематическое уравнение движения: уравнение для координаты и скорости. (Если тел несколько, уравнения движения пишутся для каждого тела). Для криволинейного движения (по необходимости) запишите формулы линейной и угловой скоростей, частоты, периода, ускорения.
Определите начальные условия (координаты и скорость в начальный момент времени), а также проекции ускорения и скорости на оси координат и подставьте эти величины в уравнение движения. (Для криволинейного движения отобразите начальные условия на рисунке).
Определите дополнительные условия, т.е. координату или скорость для какого- то момента времени и подставьте эти величины в уравнение движения. По необходимости введите дополнительные обозначения, запишите справочные данные.
Решите полученную систему уравнений относительно искомых величин.
Выполните вспомогательный рисунок;
Запишите формулу средней скорости в общем виде, а затем применительно к задаче;
Определите начальные условия для каждого участка пути: скорость, пройденный путь, время прохождения;
По необходимости введите дополнительные обозначения;
Найдите неизвестные величины и подставьте их в формулу средней скорости;
Подставьте в формулу численные значения и найдите искомую величину.
| № п/п | Алгоритм | Выполнение последовательности алгоритма. |
| 1 | Выберите систему отсчета: тело отсчета, систему координат, прибор для измерения времени (положительное направление оси) или начертите предложенный к задаче график (или выполните вспомогательный рисунок); | Выберем тело отсчета О, с которым свяжем ось х и укажем положительное направление (к этому чертежу вернемся в пункте 3) 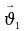   
 Х Х
|
|     2 2
| Определите вид движения вдоль каждой оси и напишите кинематические уравнения движения: уравнения для координаты и скорости. (Если тел несколько, уравнения движения пишутся для каждого тела). Для криволинейного движения   запишите (по необходимости формулы: линейной и угловой скоростей, частоты, периода, ускорения); запишите (по необходимости формулы: линейной и угловой скоростей, частоты, периода, ускорения);
| Запишем уравнение движения в общем виде: А) для прямолинейного равномерного движения: 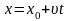 ; ; Б) для прямолинейного равноускоренного движения: 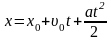 ; ;
В) т.к. в уравнениях движения данной задачи время в первой степени, следовательно, движение прямолинейное равномерное; Г) запишем кинематические уравнения для велосипедиста и мотоциклиста: 
  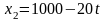
|
| 3 | Определите начальные условия (координаты и скорость в начальный момент времени), а также проекции ускорения и скорости на оси координат и подставьте эти величины в уравнение движения. (Для криволинейного движения начальные условия отобразить на рисунке); | Из уравнения прямолинейного равномерного движения записанного в общем виде (п.2А) следует, что у велосипедиста ( ) скорость ) скорость  и направлена по оси ОХ (т.к. скорость величина положительная). и направлена по оси ОХ (т.к. скорость величина положительная). Для мотоциклиста (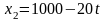 ) скорость ) скорость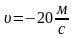 и направлена против оси ОХ (т.к. скорость величина отрицательная). и направлена против оси ОХ (т.к. скорость величина отрицательная). Изобразим скорости на чертеже в пункте 1. |
| 4 | Определите дополнительные условия, т.е. координату или скорость для какого-то момента времени и подставьте эти величины в уравнение движения. По необходимости введите дополнительные обозначения, запишите справочные данные; |
Когда тела встретятся: 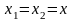
|
| 5 | Решить полученную систему уравнений относительно искомых величин | А) Запишем полученную систему уравнений: 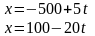
Б) Если равны левые части этих уравнений, то равны и правые их части. Приравниваем правые части и решаем уравнение:

В) Подставляем время t в любое уравнение движения (А), например: или Мы видим, что результаты одинаковые. Это действительно так, ведь велосипедист и мотоциклист встретятся в точке, координата которой х.
Ответ: координата точки встречи велосипедиста и мотоциклиста . . |
Две лодки движутся навстречу друг другу, первая – по течению реки, вторая против течения. Скорости лодок относительно воды 4 м/с и 2 м/с, скорость течения реки 2 м/с. Определите скорость лодок относительно берега.
| № п/п | Алгоритм | Выполнение последовательности алгоритма. |
| 1 | Выберите систему отсчета: тело отсчета, систему координат, прибор для измерения времени (положительное направление оси) или начертите предложенный к задаче график (или выполните вспомогательный рисунок); | Выберем тело отсчета О, с которым свяжем ось Х и укажем положительное направление. (к рисунку вернемся в п.3)
   
 
  
 X X
|
| 2 | Определите вид движения вдоль каждой оси и напишите кинематические уравнения движения: уравнения для координаты и скорости. (Если тел несколько, уравнения движения пишутся для каждого тела). Для криволинейного движения запишите (по необходимости формулы: линейной и угловой скоростей, частоты, периода, ускорения); | А) Запишем уравнение скорости в общем виде: , где  -скорость тела относительно неподвижной системы отсчета; -скорость тела относительно неподвижной системы отсчета;
- (скорость течения реки) скорость подвижной системы отсчета (ПСО) относительно неподвижной системы отсчета(НСО) ��  - скорость тела относительно подвижной системы отсчета; - скорость тела относительно подвижной системы отсчета; Б) Запишем уравнение скорости для каждой лодки: �� , где �� , где ��  - скорость первой лодки относительно ПСО; - скорость первой лодки относительно ПСО;  - скорость первой лодки относительно НСО - скорость первой лодки относительно НСО  , где , где  - скорость второй лодки относительно ПСО; - скорость второй лодки относительно ПСО;  - скорость второй лодки относительно НСО; - скорость второй лодки относительно НСО;
|
| 3 | Определите начальные условия (координаты и скорость в начальный момент времени), а также проекции ускорения и скорости на оси координат и подставьте эти величины в уравнение движения. (Для криволинейного движения начальные условия отобразить на рисунке; | А) На рисунке изобразим скорости лодок и течения реки относительно НСО; Б) Найдем проекции скоростей на ось ОХ для каждой лодки: скорость  - направлена по оси ОХ, значит ее проекция положительная; - направлена по оси ОХ, значит ее проекция положительная; скорость  - направлена против оси ОХ, значит ее проекция отрицательная. - направлена против оси ОХ, значит ее проекция отрицательная. В) Запишем уравнения скоростей лодок в проекциях на ось Х: 

|
| 4 | Определите дополнительные условия, т.е. координату или скорость для какого-то момента времени и подставьте эти величины в уравнение движения. По необходимости введите дополнительные обозначения, запишите справочные данные. |
_____________ |
| 5 | Решить полученную систему уравнений относительно искомых величин | Подставим в уравнение скоростей численные значения и определим скорости лодок относительно берега:  =6 м/с =6 м/с
 =4 м/с =4 м/с
Ответ: 6 м/с 6 м/с  4 м/с 4 м/с |

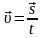


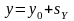
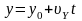
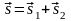 - закон сложения перемещений;
- закон сложения перемещений; 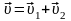 - закон сложения скоростей
- закон сложения скоростей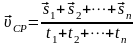

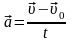

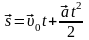
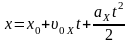
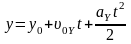
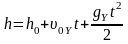
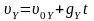
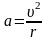
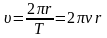

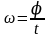
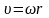
 , а мотоциклиста
, а мотоциклиста 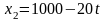 . Определить координату точки их встречи.
. Определить координату точки их встречи.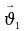



 Х
Х


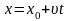 ;
;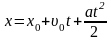 ;
;
 и направлена по оси ОХ (т.к. скорость величина положительная).
и направлена по оси ОХ (т.к. скорость величина положительная).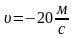 и направлена против оси ОХ (т.к. скорость величина отрицательная).
и направлена против оси ОХ (т.к. скорость величина отрицательная).