Древняя поговорка мудро называла повторение «матерью учения». И действительно, без повторения пройденный материал не закрепится в сознании учеников, не станет новой ступенью в изучении предмета. Особенно это важно в математике. Как сделать уроки повторения не скучным прохождением не раз пройденного, а интересным и увлекательным занятием. Об этом хорошо знают те, кто использует на уроках презентации.
Источник презентации:
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Межпредметный урок по физике и алгебре "Векторы.Сила".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
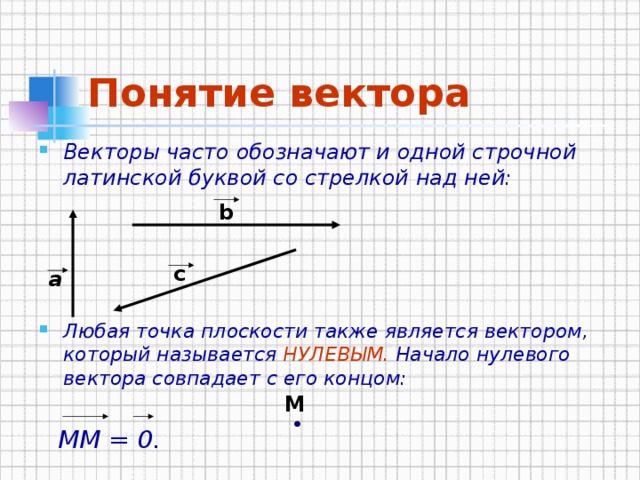
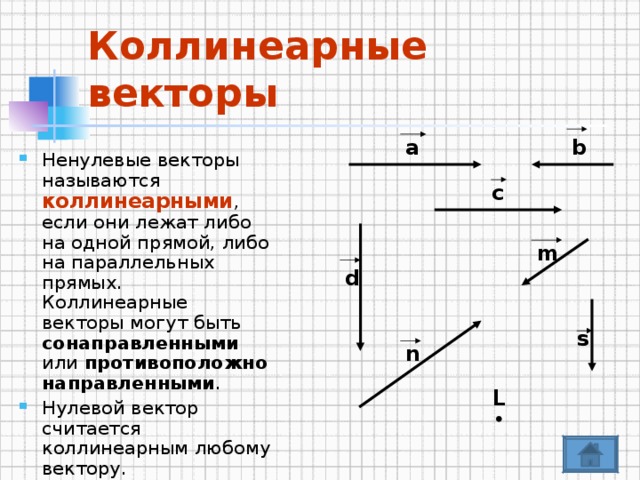
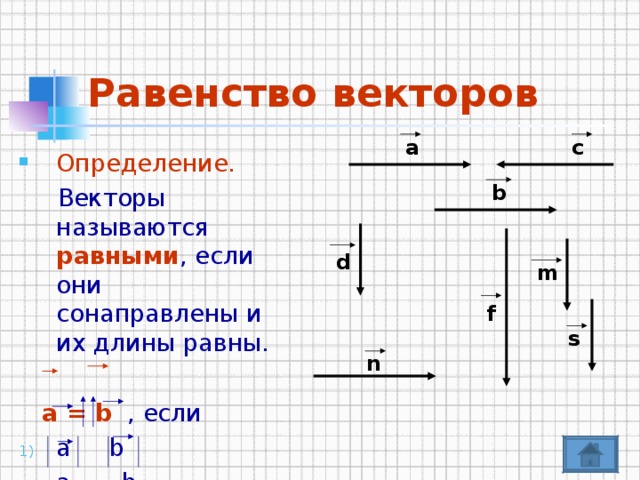
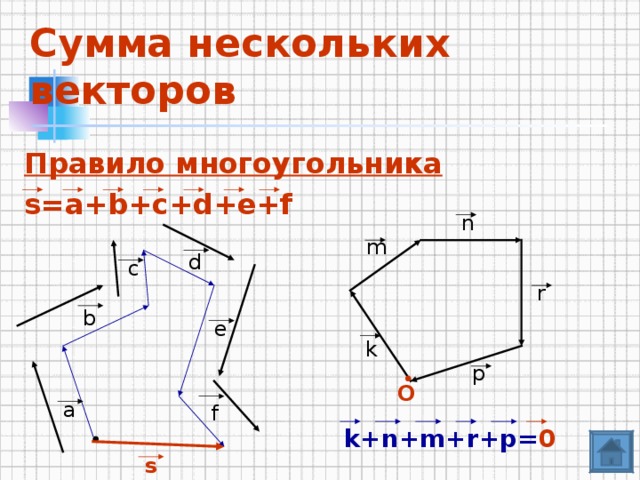
«Межпредметный урок по физике и алгебре "Векторы.Сила". »
Полезное для учителя
Распродажа видеоуроков!
1610 руб.
2690 руб.
1990 руб.
3320 руб.
1670 руб.
2780 руб.
1570 руб.
2620 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства