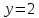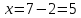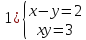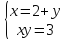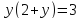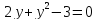| 2. Актуализация опорных знаний и способов действий | Учитель задает вопросы ученикам.
Учитель заранее записал на доске системы уравнений.
| - Итак, начнем. Откройте тетради, запишите число, классная работа. - На прошлом уроке мы изучали методы решения систем, в которых содержатся уравнения второй степени. Сегодня мы закрепим полученные знания. Поэтому записываем тему урока: «Простейшие системы, содержащие уравнения второй степени». - Скажите, какими способами мы можем решить систему уравнений? 1)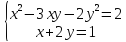 2)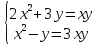 - Обратите внимание, на доске записаны системы уравнений. - Проанализируем первую систему уравнений. Какой алгоритм решения имеет данная система?
- Как называется такой способ?
- Проанализируем вторую систему уравнений. Как можно её решить?
- Какой алгоритм решения имеет данная система уравнений, если решать способом сложения?
| Записывают в тетради число, классная работа. Слушают учителя и записывают тему урока.
-Методом алгебраического сложения, методом подстановки, по обратной теореме Виета, графическим методом.
Отвечают на вопросы учителя.
- Из второго уравнения выражаем х. Подставляем полученное выражение в уравнение второй степени, получается уравнение с одной переменной. Решаем получившееся уравнение с одной переменной. Тем самым найдем у, полученное значение подставляем во второе уравнение и находим х. - Такой способ называется способом подстановки. - Данную систему можно решить способом подстановки и способом сложения.
- В первую очередь нужно выбрать, от какой переменной мы избавимся. Если при сложении уберем x^2, то необходимо второе уравнение умножить на -2, чтобы оно было равносильно первому уравнению. При сложении двух уравнений, получится линейное уравнение. Решив его, найдем корни и подставим в любое из уравнений.
| Регулятивные: умение формулировать и аргументировать свое мнение. Коммуникативные: владение устной и письменной речью. Познавательные: установление причинно-следственных связей. |
| 3. Закрепление изученного материала |
Учитель вызывает одного ученика к доске.
Обращается к классу
Учитель вызывает одного ученика к доске.
Учитель вызывает одного ученика к доске.
Учитель вызывает одного ученика к доске.
Учитель вызывает одного ученика к доске.
Учитель вызывает одного ученика к доске.
Задает вопросы ученикам. | - Алгоритм решения мы проговорили, теперь решим эти две системы уравнений. Записываем в тетрадь первую систему уравнений. К доске пойдёт…
- Решая систему уравнений, проговаривай каждое действие.
- Каким способом будем решать? - Что делаем в первую очередь?
- У всех такое уравнение получилось? - Решаем дальше.
- Записываем ответ. - Записываем в тетрадь вторую систему уравнений. К доске пойдёт …
- Решая систему уравнений, проговаривай каждое действие.
- Каким способом будем решать? - Что для этого делаем? - Вы должны понимать, что ваша задача сделать так, чтобы при сложении двух уравнений одна переменная убралась.
- Записываем ответ. - Обратимся к учебнику на странице 137 и записываем №500 (1,3): Решить систему уравнений 1)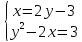 3)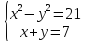
- Каким способом будем решать? - Что получится?
-Записываем ответ.
- Каким способом будем решать? - Что получится?
- Записываем ответ.
- Записываем следующий № 501 (1,3): Решить систему уравнений 1)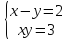 3) 3)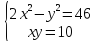 5)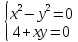
-Каким способом будем решать?
- Записываем ответ.
-Каким способом будем решать?
- Какое уравнение у нас получилось? - Как решать такие уравнения?
- Что тогда у нас получится?
- Записываем ответ. | Записывают в тетрадь первую систему уравнений
Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 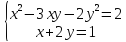 - Способом подстановки. - Со второго уравнения выражаем х, получим: 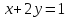 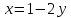 Подставляем в первое уравнение вместо х, получим: 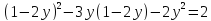 Раскрываем скобки и приводим подобные 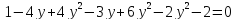 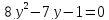 - Квадратное, не приведенное. Отвечает класс - Да. Ученик продолжает решать у доски Решаем через дискриминант 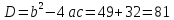 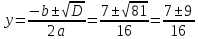 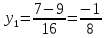 , , 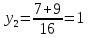 Найденные корни подставляем во второе уравнение 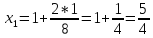 =1,25 =1,25 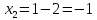 Ответ: (1.25; 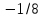 ); (-1:1) ); (-1:1) Записывают в тетрадь вторую систему уравнений
Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 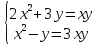
- Способом сложения. - Нужно избавится от одной переменной, например, от 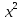 . Для этого нужно умножить второе уравнение на . Для этого нужно умножить второе уравнение на -2, чтобы сделать уравнения равносильными. 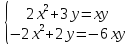 Складываем уравнения 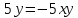 Переносим все в левую часть и приводим подобные 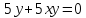 Выносим 5у за скобки и находим корни 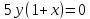 у=0 1+х=0 х=-1 Подставляем корни в любое из уравнений. Подставим во второе, так как оно проще у=0 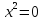 х=0 х=0 х=-1 1-у=3у*(-1) 1-у=-3у у=-0,5 Ответ: (0;0) (-1; -0,5) Открывают учебник, записывают номер задания в тетрадь. Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 1)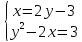 - Способом подстановки 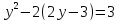 Раскроем скобки и приведем подобные 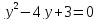 Решаем через дискриминант 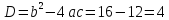 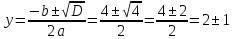 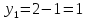 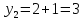 Найденные корни подставим в первое уравнение 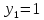 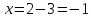 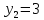 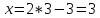 Ответ: (-1;1) (3;3) Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 3)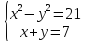 - Способом подстановки Выразим из второго уравнения х и подставим во второе уравнение 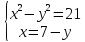 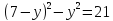 Раскрываем скобки и приводим подобные 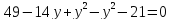 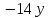 =-28 =-28 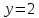 Полученный корень подставляем во второе уравнение 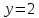 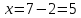 Ответ: (5;2)
Записывают следующий номер.
Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 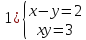 - Способом подстановки Выразим из первого уравнения х и подставим, полученное выражение в первое уравнение 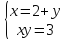 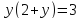 Раскрываем скобки и приводим подобные 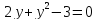  Решаем через дискриминант  , ,  Полученные корни подставляем в первое уравнение y=-3 x=2-3=-1 y=1 x=2+1=3 Ответ: (-1;-3) (3;1) Один из учеников выходит к доске для решения системы уравнений, проговаривая каждое действие 3) 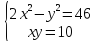 - Способом подстановки Выразим из второго уравнения х и подставим выражение в первое уравнение  Умножим обе части на    - Биквадратное - Нужно сделать замену   Получилось квадратное уравнение. Решаем через дискриминант  , ,  Найденные корни подставляем в замену  - нет корней - нет корней  Полученный корень подставляем во второе уравнение     Ответ: (5;2) (-5;-2) | Регулятивные: умение применять полученные знания; осуществлять контроль по результату, выявление допущенных ошибок в процессе работы и обоснование способов их исправления. Познавательные: умение ориентироваться в понятиях. Коммуникативные: взаимодействие в группе; выражение своих мыслей, аргументация своих мнений; умение слушать других и быть готовым принять другую точку зрения. |
| 5. Подведение итогов урока | Задает вопросы ученикам.
Прощается с классом. | - Подводя итоги урока, оцените себя, ответив на следующие вопросы. - Какие способы решения систем уравнения мы сегодня использовали? -Опишите алгоритм решения систем уравнений методом подстановки.
-Опишите алгоритм решения систем уравнений методом сложения.
- Все ли понятно было при решении систем уравнений? - На этом наш урок закончен. Ученики, которые выходили к доске, подойдите ко мне с дневниками. До свидания! | Учащиеся отвечают на вопросы: - Способ подстановки и сложения. - 1. Из первого уравнения данной системы выражаем любую переменную. 2. Подставляем это выражение во второе уравнение. 3. Решаем полученное уравнение. 4. Подставляем полученный результат в выражение, полученное в первом пункте. 5. Проверяем полученное решение, для этого подставляем найденные числа в исходную систему. 1.Уравняем модули коэффициентов при одном из неизвестных (если необходимо). 2. Сложим уравнения. 3. Решим полученное уравнение с одной переменной, найдем неизвестное. 4. Подставим найденное на втором шаге значение переменной в одно из уравнений исходной системы, найдем второе неизвестное. 5. Запишем ответ. - Да. Прощаются с учителем. Подходят с дневниками. | Коммуникативные: умение выражать свои мысли. Регулятивные: контроль и оценка своей деятельности в рамках урока. Познавательные: построение речевого высказывания в устной форме, контроль и оценка процесса и результатов деятельности. |
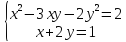
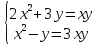
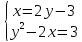
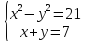
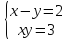 3)
3)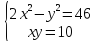
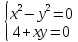
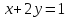
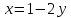
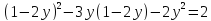
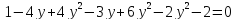
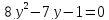
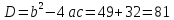
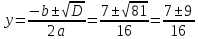
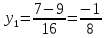 ,
,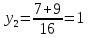
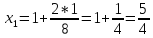 =1,25
=1,25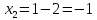
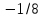 ); (-1:1)
); (-1:1)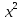 . Для этого нужно умножить второе уравнение на
. Для этого нужно умножить второе уравнение на 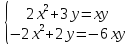
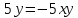
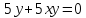
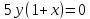
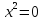 х=0
х=0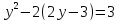
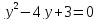
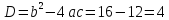
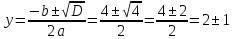
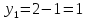
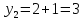
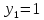
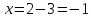
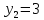
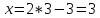
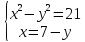
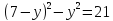
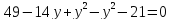
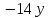 =-28
=-28