| Этапы урока | Время | Деятельность учащихся | Деятельность учителя | Универсальные учебные действия |
| 1.Этап мотивации (самоопределения) к учебной деятельности. | 1-2 мин | Показывают готовность к уроку. Отвечают на вопросы учителя. Решают предложенные уравнения Включаются в деловой ритм урока. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Чему мы научились на прошлом уроке? [решать квадратные уравнения по формулам] Решите уравнения. | Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование учебного сотрудничества с учителем и сверстникам |
| 2.Этап актуализации и пробного учебного действия. | 5-7 мин | Отвечают на вопросы учителя. Обмениваются тетрадями и делают проверку. Самостоятельно выполняют индивидуальные задания на применение новых знаний, запланированных для изучения на данном уроке. Работают в парах. У каждого на парте карточка с квадратными уравнениями. Учащиеся решают уравнения и записывают в таблицу : корни уравнений, сумму корней, произведение корней. Фиксируют возникшее затруднение в выполнении заданий
| Повторим все. Что мы знаем о квадратных уравнениях. Задаёт вопросы. Что записано на доске? [Квадратные уравнения.] 2. Докажите, что данные уравнения квадратные. 3.Какие виды квадратных уравнений записаны? [Приведенные и неприведенные уравнения] Решите данные уравнения. Проводится взаимопроверка. Учитель называет правильные ответы. Оценка 5 выставляется за все правильно решенные задания и т.д. Учитель предлагает учащимся заполнить таблицу. [ на партах карточки] | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; Познавательные: самостоятельное выделение и формулирование познавательной цели. Логические – формулирование проблемы. |
| 3.Этап выявления места и причины затруднения. | 2-3 мин | Анализируют и проговаривают вслух, что и как они делали; фиксируют каких знаний и умений недостает для решения уравнений.
| Анализирует причины затруднений и помогает в выборе знания, которого недостает | Регулятивные: целеполагание, прогнозирование; Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Личностные |
| 4.Этап построения проекта выхода из затруднения. | 5 мин | Учащиеся сравнивают найденные для каждого уравнения сумму и произведение корней с коэффициентами соответствующего уравнения. Находят зависимость между ними. Формулируют утверждение. Учащиеся формулируют тему урока [Теорема Виета]
.
| Для каждого уравнения вы нашли корни, сумму корней, произведение корней. Сравните сумму и произведение корней с коэффициентами уравнения в первом столбике. Какая существует зависимость между корнями приведенного квадратного уравнения и его коэффициентами? Если учащиеся затрудняются, учитель помогает им. Сформулируйте утверждение. Историческая справка. Впервые зависимость между корнями и коэффициентами квадратного уравнения установил знаменитый французский ученый Франсуа Виет (1540-1603 гг). Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И хотя математика была его увлечением, хобби, благодаря упорному труду он добился больших результатов. Виет в 1591 г. ввел буквенные обозначения для неизвестных и коэффициентов уравнений, стало возможным свойства уравнений и корней записывать общими формулами. Недостатком алгебры Виета было то, что он признавал только положительные числа. Чтобы избежать отрицательных решений, он заменял уравнения или искал искусственные приемы решения, что отнимало много времени, и усложняло решение. Много разных открытий сделал Виет, но сам он больше всего дорожил установлением зависимости между корнями и коэффициентами квадратного уравнения, т.е. той зависимостью, которая называется «теоремой Виета». Назовите тему урока.[Теорема Виета] [Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, произведение корней равно свободному члену.] | Предметные: формирование навыков построения математических моделей и решения практических задач Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания Личностные: планирование учебной деятельности |
| 5.Этап реализации построенного проекта. | 7 мин | Учащиеся слушают доказательство теоремы . Формулируют теорему обратную теореме Виета для приведенного уравнения, а затем для произвольного квадратного уравнения. Проверяют равенства для уравнений 3 и 4 из самостоятельной работы.
| Докажем теорему Виета. 1. Дано: х2 + рх + q = 0. Доказать: 1) х1 + х2 = –р; 2) х1 х2 = q. 2. Сформулируйте обратную теорему Виета. Если числа m и n таковы, что их сумма равна –р, а произведение равно q, то эти числа являются корнями уравнения х2+рх+q=0. 3. Сформулируйте теорему Виета для произвольного квадратного уравнения. ах2 + bx + c = 0, а 0, х2 + 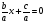 . . 1) х1 + х2=–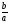 ; 2) х1 х2 = ; 2) х1 х2 = 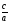 . . 4. Проверьте равенства для уравнений 3 и 4 из самостоятельной работы. | Предметные: формирование навыков построения математических моделей и решения практических задач Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Познавательные: моделирование, решение проблемы, построение логических цепей, анализ, умение структурировать знания |
| 6.Этап первичного закрепления с проговариванием во внешней речи; | 5-7 мин | Учащиеся выполняют задания у доски, при этом проговаривают вслух выполняемые шаги : алгоритм нахождения суммы и произведения корней, нахождение неизвестного коэффициента.
| 1. Проверьте, правильно ли найдены корни квадратного уравнения: а) х2 + 3х – 40 = 0, х1 = –8, х2 = 5; б) х2 + 2х – 3 = 0, х1 = –1, х2 = 3; в) 2х2 – 5х – 3 = 0, х1 = –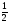 , х2 = 3. , х2 = 3. 2. Найдите корни квадратного уравнения, применяя теорему, обратную теореме Виета: а) х2 – 6х + 5 = 0; б) х2 – 7х + 12 = 0; в) х2 – х – 12 = 0. 3. Составьте приведенные квадратные уравнения, если его корни равны: а) х1 = –3, х2 = 1; б) х1 = –3, х2 = –4; в) х1 = 5, х2 = 6. 4. Проверьте выполнимость теоремы Виета для уравнения: 1) х2 – 2х – 9 = 0, р = –2, q = –9. х1 =1 – 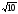 , х2 = 1 + , х2 = 1 + 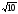 , , х1 + х2 = 2, х1 х2 = –9. 2) 2х2 + 7х – 6 = 0, р = 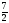 , q = –3. , q = –3. х1=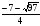 , х2= , х2=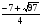 , , х1 + х2=–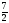 , х1 х2 = –3. , х1 х2 = –3. 5. Найдите: х2, р, если известно х2 + рх – 35 = 0, х1 = 7. Решение. х1х2 = –35, 7х2 = –35, х2 = –5; х1 + х2= –р, 7–5=–р, р= –2. Ответ: х2 = –5, р = –2. | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками Регулятивные выделение и осознание того, что усвоено, что ещё подлежит усвоению Познавательные: |
| 7.Этап самостоятельной работы с самопроверкой по эталону | 10 мин | Учащиеся выполняют предложенные учителем задания по учебнику. Проверяют правильность выполнения заданий под руководством учителя. Если есть ошибки, то исправляют их.
| открыли учебник на стр. 130. № 580, № 581, № 585, № 586 организовывает самопроверку учащимися своих решений ; создает (по возможности) ситуацию успеха для каждого ребенка; для учащихся, допустивших ошибки, предоставляет возможность выявления причин ошибок и их исправления | Регулятивные контроль, оценка Познавательные: формулирование проблемы
|
| 8. Рефлексия учебной деятельности.
| 5 мин | Учащиеся отвечают на вопросы учителя
Скорее всего, ученики скажут, что число 2. [ по дискриминанту или выделением квадрата двучлена ] Плюс [Нет, х1х2 = –9, значит, корни разных знаков.] [Да, можно, потому что х1+х2=20.]
Учащиеся записывают домашнее задание
| Вопрос 1. Можно ли, не решая самого уравнения x2–2x+3=0, сказать, чему равна сумма его корней? Скорее всего, ученики скажут, что число 2. Однако этот ответ неверен, так как это уравнение вообще не имеет корней: x2–2x+3=x2–2x+1+2=(x–1)2+220. Следовательно, прежде чем ответить на вопрос о сумме и произведении корней, необходимо проверить, существуют ли корни у заданного квадратного уравнения. Как ? [ по дискриминанту или выделением квадрата двучлена ] Вопрос 2. Каков по знаку дискриминант уравнения х2–2x–9=0? Вопрос 3. Могут ли оба корня уравнения х2–2x–9=0 быть положительными? [Нет, х1х2 = –9, значит, корни разных знаков.] Вопрос 4. Можно ли утверждать, что модуль положительного корня уравнения х2–2x–9=0 больше модуля отрицательного? [Да, можно, потому что х1+х2=20.]
Домашнее задание: № 582, № 587, № 588. Творческое задание для сильных учеников: «Доказать, что если в квадратном уравнении ах2+bx+c=0: 1) а + b + c = 0, то х1 = 1, х2 = 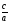 ; ; 2) а – b + c = 0, то х1 = –1, х2= –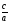 ». ». | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Регулятивные: планирование, контроль, оценка, коррекция, выделение и осознание того, что усвоено, что ещё подлежит усвоению Познавательные: умение структурировать знания Личностные: смыслообразование. |
«Теорема Виета».
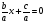 .
.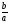 ; 2) х1 х2 =
; 2) х1 х2 = 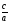 .
.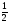 , х2 = 3.
, х2 = 3.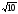 , х2 = 1 +
, х2 = 1 + 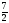 , q = –3.
, q = –3.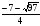 , х2=
, х2=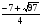 ,
, 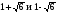
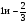
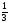
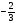
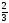
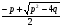 и
и 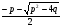
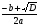 и
и