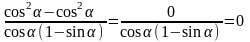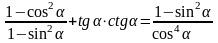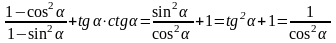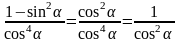Рассмотрено на заседании предметно-цикловой комиссии общеобразовательных дисциплин (корпус №1) от «____» ______ 2019 г. протокол № _____
Тема урока. Основные тригонометрические тождества
-повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
-научить применять полученные знания при упрощении тригонометрических выражений, доказательстве тождеств.
Оборудование: экран, компьютер, проектор, презентация, учебник Башмаков М.И. «Математика: учебник для учреждений нач. и сред.проф.образования, задачник Башмаков М.И. «Математика. Задачник: учебное пособие для образовательных учреждений нач. и сред.проф.образования.
- групповая технология.
Методы: словесно-наглядные, показательно-иллюстративные с применением мультимедийных технологий, практические.
| № п/п | Этапы работы с указанием цели | Формы и методы обучения, контроля | Наглядные пособия, ТСО, дидактический материал | Деятельность преподавателя | Деятельность обучающегося | Ожидаемые результаты | Время (90 мин.) |
| Организационный момент. Взаимное приветствие преподавателя и обучающихся. Цели: создание благожелательной атмосферы занятия, быстрого включения в работу |
| Презентация | Приветствие, проверка подготовленности обучающихся к занятию, их настроя на работу; организация внимания и готовности к занятию, проверка отсутствующих | Включаются в деловой ритм занятия | Настраиваются на занятие | 5 мин |
| Актуализация опорных знаний. Цели: повторение изученного ранее материала
| Фронтальный опрос | Презентация | 1.Организует работу у доски двух обучающихся с целью проверки выполнения домашнего задания 2. Организует проведение устной математической разминки для проверки усвоения раннее изученного материала
Слайд 1: «Математическое лото». Переведите в градусную меру угол: а) π; б) 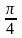 ; в) ; в) 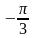 ; г) ; г) 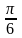 ; д) ; д) 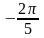 2. Переведите в радианную меру угол: а) 90º б) – 180º в) 360º г) – 270º д) 720º 3. Дайте определение sin α, cos α, tg α, ctg α. 4. Вычислите: а) 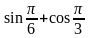 б) 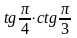 в) 4сos 90º – 8sin 30º г) ctg260º + 2 5. Какое из чисел больше 0? а) sin 340º б) cos (–120º) в) sin 50º г) tg 170º 6. Какие из выражений не имеют смысла? а) sin 90º б) cos 0º в) tg 90º г) ctg 0º
3.Предлагает проверить домашнее задание, выполненное на доске
| 1. Двое обучающихся работают у доски.
2. Отвечают на поставленные вопросы. Выполняют задания .
3. Проверяют решения.
| Оценивают достигнутый результат .Формулируют понятия. Оценивают ответы других обучающихся. | 15 мин |
| Постановка учебной задачи. Цели: подготовка обучающихся к усвоению нового материала
| Словесно-наглядный метод. Фронтальный опрос | Презентация | Предлагает ответить на устные вопросы из домашнего задания: сформулировать определения понятий тождества, тождественного выражения и тождественного преобразования. Слайд 2: Тождеством называется равенство, справедливое при всех допустимых значениях входящих в него букв. Допустимые значения букв – это значения, которые могут принимать буквы в данном выражении. Выражения, находящиеся в левой и правой частях тождества, называются тождественными. Замена некоторого выражения другим, ему тождественным, называется тождественным преобразованием данного выражения.
- Как вы думаете, как связаны эти понятия с изучаемым материалом? (Предполагаемый ответ: тождества и тождественные выражения будут содержать тригонометрические функции, и мы будем преобразовывать такие выражения и доказывать тождества).
Преподаватель объявляет тему урока: «Основные тригонометрические тождества».
| Отвечают и проверяют правильность своих ответов с помощью слайда 2.
Предлагают варианты ответа.
| Оценивают достигнутый результат | 10 мин |
| Изучение нового материала Цели: получение новых знаний Постановка проблемной ситуации Цели: совместная формулировка целей урока | Словесно-наглядный метод, практический | Презентация | Слово преподавателя: - При изучении темы «Зависимость между тригонометрическими функциями одного и того же аргумента мы уже встретились с тождествами. Например, это все формулы зависимости межу синусом, косинусом, тангенсом и котангенсом одного и того же угла. Сегодня мы выясним, как можно использовать эти формулы при упрощении тригонометрических выражений и доказательстве тригонометрических тожеств.
Слайд 3: sin2 α + cos2 α = 1 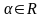 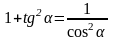 cos α ≠ 0, cos α ≠ 0, 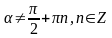 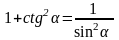 sin α ≠ 0, α ≠ πn, sin α ≠ 0, α ≠ πn,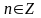
tg α ∙ ctg α = 1 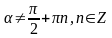 , , 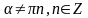
Преподаватель задаёт вопрос группе: - При каких допустимых значениях α справедливы эти тождества?
Слово преподавателя: - Для выполнения тождественных преобразований тригонометрических выражений можно использовать не только данные тригонометрические тождества, но и другие формулы тригонометрии, а также алгебраические преобразования, например, действия с дробями, вынесение за скобки общего множителя, формулы сокращённого умножения и т. д.
- Выполните следующие задания с помощью тождественных преобразований
Слайд 4: Упростите выражение: а) 1 – sin2 x = cos2 x б) cos2 β – 1 = – sin2 β в) tg x ∙ ctg x + 4 = 5 г) cos α ∙ tg α = sin α д) (1 – cos x)(1 + cos x) = 1 – cos2 x = sin2 x е) sin2 α + 2sin α ∙ cos α + cos2 α = (sin α + cos α)2 2. Выразите через sin2α: a) (1 – cos2 α) + sin2 α = 2sin2 α б) 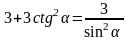 3) Выразите через tg α: a)  б) 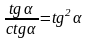
Слово преподавателя: -Тождественные преобразования используются при доказательстве тождеств. Какие вы знаете способы доказательства тождеств?
Слайд 5: Способы доказательства тождеств: - преобразование правой части к левой; - преобразование левой части к правой; - установление того, что разность между правой и левой частями равна нулю; - преобразование левой и правой части к одному и тому же выражению.
| Называют формулы, при необходимости обращаются к упражнениям из домашнего задания.
Называют допустимые значения α, при этом постепенно появляется правая часть слайда 3.
Отвечают. Правая часть равенства появляется при ответе учащихся.
Отвечают, проверяют ответы с помощью слайда 5.
| Оценивают достигнутый результат | 25 мин. |
| Закрепление изученного материала. Цели: применении полученных знаний | Практический метод | Презентация | Предлагает задания . Организует работу обучающихся, контролирует и проверяет выполнение задания
Слайд 6: Задача 1. Доказать, что при α ≠ πn, 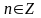 , справедливо равенство , справедливо равенство sin2 α + ctg2 α + cos2 α = 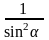 Доказательство: sin2 α + ctg2 α + cos2 α = 1 + ctg2 α = 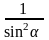 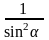 = = 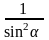
Что и требовалось доказать.
Слайд 7: Задача 2. Доказать тождество cos2 α = (1 – sin α)(1 + sin α). Доказательство: (1 – sin α)(1 + sin α) = 1 – sin2 α = cos2 α cos2α = cos2α Что и требовалось доказать.
Преподаватель вызывает к доске двух учащихся.
Задача 3. Доказать тождество: 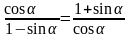
Доказательство: 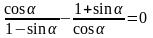
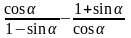 = =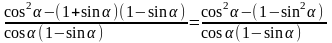 = = = 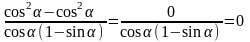 0=0. Что и требовалось доказать.
Задача 4. Доказать тождество: 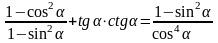
Доказательство: 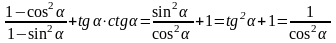
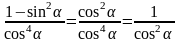

Что и требовалось доказать.
| Доказывают равенство с помощью преподавателя, записывают в тетрадь.
Устно проводят доказательство, затем записывают его в тетрадь.
Выполняют задачи 3 и 4 на закрытой части доски. Остальные самостоятельно решают эти задачи в тетрадях.
| Выработка навыков работы с тригонометрическими выражениями. Повышение качества знаний обучающихся через применение средств ИКТ. | 20 мин |
| Домашнее задание Цели: повышение качества знаний обучающихся, развитие самостоятельности в обучении | Словесно-наглядный метод | Презентация | 1.Упростите выражение: tg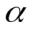 cos cos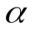 2.Вычислите: 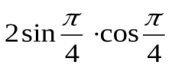
3.Решите уравнение:sinx=1 4.Упростите выражение: 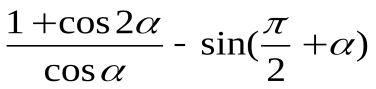
5.Вычислите: 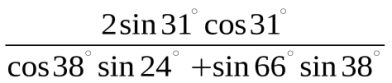
| Записывают домашнее задание в тетради | Повышение качества знаний обучающихся, развитие самостоятельности в обучении | 5 мин |
| 7. | Подведение итогов: Цели: проанализировать деятельность обучающихся, дать оценку знаний, успешности в достижении цели | Рефлексия. | Презентация | Слово преподавателя: - Пришло время подвести итоги работы. Продолжите фразу: «Сегодня на уроке я повторил…» «Сегодня на уроке я узнал…» «Сегодня на уроке я научился…» «Сегодня на уроке я закрепил…»
Преподаватель отмечает положительные и отрицательные моменты работы учащихся на уроке, типичные ошибки; выставляет и комментирует оценки.
| Слушают преподавателя, получают оценки | Рефлексия | 10 мин |
Используемая литература.
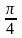 ; в)
; в) 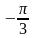 ; г)
; г) 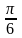 ; д)
; д) 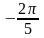
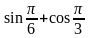
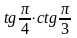
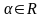
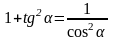 cos α ≠ 0,
cos α ≠ 0, 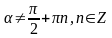
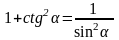 sin α ≠ 0, α ≠ πn,
sin α ≠ 0, α ≠ πn,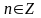
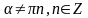
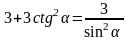

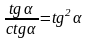
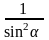
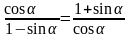
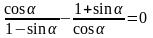
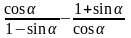 =
=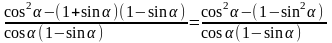 =
=