| - Итак, начнем. Откройте тетради, запишите число, классная работа. - Сегодня на уроке мы будем изучать новый материал. Перед тем, как перейти к новой теме, ответьте на несколько вопросов. Учитель задаёт ученикам вопросы - Что такое функция?
- Что называют графиком функции?
- С какими видами функции вы знакомы? - Что называется линейной функцией?
- Что называется квадратичной функцией?
- С каким видом квадратичной функции вы уже работали? - Как это функция получилась и как она называется?
- Сегодня вы познакомитесь с новым видом квадратичной функции. Поэтому записываем новую тему: «Функция 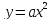 и её свойства». и её свойства». | Записывают в тетради число, классная работа.
Отвечают на вопросы учителя - Функция – зависимость одной переменной величины от другой. - Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям независимой переменной, а ординаты – соответствующим значениям функции. - С линейной и квадратичной.
- Линейной функцией называется функция вида 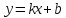 . . - Квадратичная функция – это функция 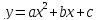 , где , где 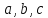 – заданные действительные числа, – заданные действительные числа, 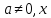 – действительная переменная. – действительная переменная. - С 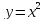
- Это функция называется параболой. Так как квадратичная функция имеет вид 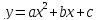 , то парабола , то парабола 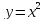 получилась при коэффициентах получилась при коэффициентах 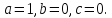
Записывают новую тему в тетрадь
|
| - При а=1 формула 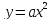 принимает вид принимает вид 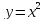 . Мы уже сказали, что графиком этой функции является парабола. Поэтому построим график функции . Мы уже сказали, что графиком этой функции является парабола. Поэтому построим график функции 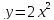 . . - Записываем задача №1: Построить график функции 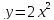 . . - Давайте вызовем кого - нибудь к доске.
Учитель вызывает к доске ученика - Как для любой другой функции, мы составляем таблицу значений.
- Теперь по данным точкам построим график.
- Соединим точки плавной кривой. - Какой график у нас получился? - Если мы сравним графики функций 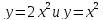 , то мы заметим, что при одном и том же х значение функции , то мы заметим, что при одном и том же х значение функции 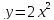 в 2 раза больше значения функции в 2 раза больше значения функции 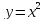 . Это значит, что каждую точку графика . Это значит, что каждую точку графика 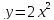 можно получить из точки графика можно получить из точки графика 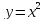 с той же абсциссой увеличением ее ординаты в 2 раза. Следовательно, график функции с той же абсциссой увеличением ее ординаты в 2 раза. Следовательно, график функции 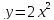 получается растяжением графика функции получается растяжением графика функции 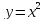 от оси Ох вдоль оси Оу в 2 раза. от оси Ох вдоль оси Оу в 2 раза. - Следующая задача: Построить график функции 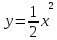 - К доске пойдёт …. Учитель вызывает к доске ученика
- Решаем также по аналогии с предыдущим примером.
- Теперь по данным точкам построим график. .
- Соединим точки плавной кривой. - Если мы сравним графики функций 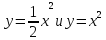 , то мы заметим, что каждую точку графика , то мы заметим, что каждую точку графика 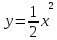 можно получить из точки графика функции можно получить из точки графика функции 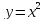 с той же абсциссой уменьшением ее ординаты в 2 раза. Следовательно, график функции с той же абсциссой уменьшением ее ординаты в 2 раза. Следовательно, график функции 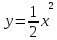 получается сжатием графика функции получается сжатием графика функции 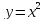 к оси Ох вдоль оси Оу в 2 раза. к оси Ох вдоль оси Оу в 2 раза. - Как вы считаете, какими будут графики 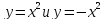 ? ?
- Куда тогда будут направлены ветви параболы графика 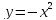 ? ?
- После всех решенных примеров, какой вывод мы можем сделать по функции 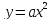 ? ?
- Теперь поговорим о свойствах функции 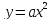 . . На доске записаны графики функции, по ним учитель рассказывает свойства - 1)Если a0, то функция 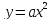 принимает положительные значения при принимает положительные значения при 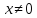 ; если a принимает отрицательные значения при ; если a принимает отрицательные значения при 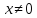 ; значение функции ; значение функции 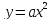 равно 0 только при х=0. равно 0 только при х=0. 2)Парабола 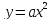 симметрична относительно оси координат. симметрична относительно оси координат. 3) Если a0, то функции 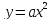 возрастает при возрастает при 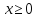 и убывает при и убывает при 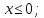 если a убывает при если a убывает при 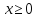 и возрастает при и возрастает при 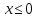 . . | Слушают учителя
Записывают первое задание в тетрадь Задача №1: Построить график функции 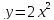 . .
Решают вместе с учителем. Один из учеников выходит к доске
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
- У нас получилась парабола.
Записывают первое задание в тетрадь Задача №2: Построить график функции 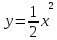 . .
Решают вместе с учителем. Один из учеников выходит к доске
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 |
- Они будут симметричными, так как график 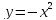 будет иметь противоположные значения графика будет иметь противоположные значения графика 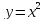 . . - Ветви параболы будут направлены вниз.
- График функции 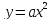 также является параболой. При a0 ветви направлены вверх, при a также является параболой. При a0 ветви направлены вверх, при a
Слушают учителя
|
| - А теперь попробуем на практике применить полученные знания. Открываем учебники на стр. 161 и записываем в тетради номера. Учитель вызывает учеников к доске для решения заданий - Разберем устно №596. Определить направление ветвей параболы: 1)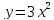 2) 2) 3) 4) 4) - Записываем в тетрадь №597 (1,3): На одной координатной плоскости построить графики функций 1) 3) Используя графики, выяснить, какие из этих функций возрастают на промежутке 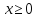 . . Учитель вызывает ученика к доске
| Открывают учебники и записывают номер в тетрадь Ученики у доски решают задания
Устно проговаривают решение задачи 1)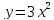 - вверх, т. к. a0 - вверх, т. к. a0 2) - вверх, т. к. a0 - вверх, т. к. a0 3) - вниз, т. к. a - вниз, т. к. a 4) -вниз, т. к. a -вниз, т. к. a
Один из учеников выходит к доске №597 (1,3) 1)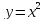 | х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 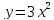
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 27 | 12 | 3 | 0 | 3 | 12 | 27 |
3)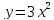 | х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 27 | 12 | 3 | 0 | 3 | 12 | 27 | 
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | -27 | -12 | -3 | 0 | -3 | -12 | -27 |
|
| Учитель сообщает домашнее задание. -Наш урок подошел к концу. Запишите домашнее задание. Учитель записывает домашнее задание на доске. П 37 стр. 157. Выучить свойства. №595(2): На миллиметровой бумаге построить график функции 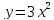 . По графику приближенно найти значения х, если у=9; 6; 2; 8; 1,3. . По графику приближенно найти значения х, если у=9; 6; 2; 8; 1,3. №597 (2,4): На одной координатной плоскости построить графики функций 1) 3) Используя графики, выяснить, какие из этих функций возрастают на промежутке 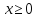 . .
| Записывают домашнее задание. |
| - Подводя итоги урока, оцените себя, ответив на следующие вопросы. - Что мы изучили на уроке?
- Все ли вам было понятно? - На этом наш урок закончен. Ученики, которые выходили к доске, подойдите ко мне с дневниками. До свидания! | Учащиеся отвечают на вопросы:
- Мы изучили новый вид квадратичной функции и её свойства.
- Да. Прощаются с учителем. Подходят с дневниками. |