Ньютон биномының қасиеттері

Ұзақ мерзімді жоспар бөлімі:

Комбинаторика элементтері

Мектеп:

Күні:

Мұғалімнің аты-жөні:

Сынып: 9

Қатысқандар саны:

Қатыспағандар саны:

Сабақ тақырыбы

Ньютон биномының қасиеттері

Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)

9.3.1.6 Ньютон биномы формуласын және оның қасиеттерін білу және қолдану;

Сабақ мақсаттары

Ньютон биномы формуласын қолданып есептер шығару арқылы, оның қасиеттерін енгізу және оны есеп шығаруда қолдану

Бағалау критерийлері

Білу: Ньютон биномы формуласын және оның қасиеттерін біледі;

Түсіну: Ньютон биномы формуласының қасиеттерін қорыту жолын түсінеді;

Қолдану: Ньютон биномы формуласының қасиеттерін есеп шығаруда қолдана алады;

Құндылықтарды дарыту

Оқушылар сыни тұрғыдан ойлай отырып, бойларына ынтымақтастық, жарқындылық, мақсаттылық, жауапкершілік қасиеттерді дарыту.

Тілдік мақсаттар

Оқушылар:

• Паскаль үшбұрышын құруды түсінеді;

• Ньютон биномы жіктелуін жазады.

• Есептің шешімін дәйектейді;

Пәнге тән лексика мен терминология:

• Паскаль үшбұрышы;

• Биномдық коэффициент;

• Ньютон биномы.

Диалог пен жазу үшін пайдалы сөздер мен тіркестер:

• Егер мен ... элементті белгілі бір ретпен орналастыратын болсам, онда ... мүмкін алмастыру пайда болады;

... мүмкін оқиғадан ... элементті таңдаудың ... тәсілі бар.

АКТ қолдану
дағдылары

Сабақтың әр кезеңінде жаңа материалды меңгеруді, қорытындылауды тиімді жүзеге асыру үшін презентациямен жұмыс және тапсырмаларды Activ Board –та орындау арқылы интерактив тақтамен жұмыстану дағдыларын дамыту.

Бастапқы білім

Комбинаториканың формулаларын және Ньютон биномы формуласын біледі.

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған іс-әрекет

Ресурстар

Сабақтың басы

5 мин

1.Ұйымдастыру сәті.

Оқушылардың сабаққа дайындығын қадағалау.

2. Жұптық жұмыс.

Мақсаты: сабақ барысында жаңа материалды меңгеруде қажетті, Ньютон биномы, формуласын еске түсіру. Тапсырмаларды сыныптасымен талдап, бір-біріне түсіндіріп, орындайды.

Мұғалімнің іс-әрекеті: Топшамалар беріп, жұпқа бөлінуін, жұптардың бірігіп тапсырмаларды орындауын қадағалау. Дұрыс жауап экраннан көрсетіледі.

Оқушының іс-әрекеті: Топшамалардың ішіндегі бірдей тапсырмалар бойынша жұбын тауып, тапсырманы орындайды.

Топшама

Қосымша №1

Сабақтың ортасы

5 мин

2 мин

10 мин

8 мин

8мин

3. Жаңа тақырыпқа кіріспе.

Мақсаты: Жаңа тақырыпты жеңіл қабылау үшін және жаңа тақырып пен өткен тақырыптың байланысын анықтау үшін мұғалімнің қойған сұрақтарына жауап беріп және тапсырмаларды орындау.

Оқушының іс-әрекеті:

*Қойылған сұрақтарға жауап береді/топшамадағы берілген тапсырманың негізінде/:

- Көпмүшенің биномдық жіктелуіндегі қосылғыштар саны қанша?

- Көпмүшенің биномдық жіктелуіндегі коэффициенттері қандай заңдылыққа бағынып тұр?

- Көпмүшенің биномдық жіктелуіндегі коэффициенттерінің қосындысының мәнін табыңыз;

- Қандай қорытынды жасауға болады?

- Көпмүшенің биномдық жіктелуіндегі кез-келген мүшесінің коэффициент анықтауға бола ма?

-Комбинаториканың негізгі формулаларын жазыңыздар;

Мұғалімнің іс-әрекеті: бағыттаушы сұрақтар қояды, жаңа материалды толық түсінуге қажетті ақпаратты жинақтау.

Нәтижені бағалау: ынталандыру

4. Оқушылармен бірге сабақтың мақсатын анықтау.

Мақсаты:Сабақ бойы оқушының зейінін шоғырландыру үшін сабақтың мақсатын оқушылармен бірге анықтау.

Оқушының іс-әрекеті: тақырыпқа кіріспе бөлімінде қойылған сұрақтарға берілген жауаптарға талдау жасай отырып, сабақтың мақсатын анықтау.

5. Жаңа тақырып. жұптық жұмыс

Мақсаты: жаңа тақырыпты өз бетінше меңгеріп көруге мүмкіндік туғызу, мұғалімнің көмегімен жаңа тақырып тапсырмаларын талқылап, формуланы оқушылардың өзі қорытып шығаратындай мүмкіндік туғызу.

Сипаты: Жұптарға тапсырма беріледі. Оқушыларға биномдық коэффициенттердің қасиеттерін өздігінен тұжырымдау ұсынылады.

1-жұп. Симметрия қасиеті.

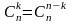
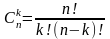Осы қасиетті тікелей формуланы пайдалана отырып дәлелдеуді ұсынылады. Оқушылар мысал келтіреді.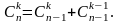

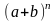2-жұп. Паскаль қасиеті.

Осы қасиеттің негізінде Паскаль үшбұрышы құрылды, оның n-ші жолында биномдық жіктелудің коэффициенттері тұрады.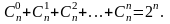

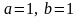3-жұп. Қосындының қасиеті.

Ньютон биномы формуласына мәні қоюды ұсынылып бағыт беріледі: 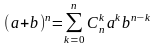Бұдан

4-жұп. Айырманың қасиеті.

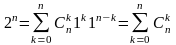
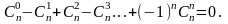
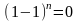Ньютон биномы формуласына а=1, b=-1 қоюды ұсынылып бағыт беріледі. Сол жақ бөлігінен , ал оң жақ бөлігінен таңбасы ауысып отыратын биномдық коэффициенттерді аламыз, бұл қасиеттің дәлелдеуі болады.

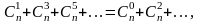Барлық теріс таңбалы коэффициенттерді формуланың сол жағына шығару арқылы жазу ыңғайлы болады: сонда қасиеттің ауызша тұжырымдауы есте оңай сақталады: “тақ номерлі биномдық коэффициенттердің қосындысы жұп номерлі биномдық коэффициенттердің қосындысына тең болады”.

5-жұп. Ньютон биномының жіктелуіндегі кез-келген мүшесінің формуласын анықтау.

Оқушының іс-әрекеті: мұғалімнің басшылығымен жаңа тақырып мазмұнын меңгеруге берілген тапсырмаларды талдайды, қасиеттерді дәлелдейді.

Мұғалімнің іс-әрекеті: жаңа материалды меңгерту, қосымша сұрақтар беру арқылы оқушыға бағыт-бағдар береді.

Бағалау: Тапсырмаларды орындау барысында оқушылар ауызша марапаттау, ынталандыру.

6. Жеке жұмыс. Бекіту тапсырмаларын орындау.

Мақсаты: Ньютон биномы формуласынның қасиеттерін есеп шығаруда қолдану; биномдық жіктелудегі белгісіз мүшесін табу үшін ақпаратты талдау және өңдеу, тапсырманы орындау барысында пайда болған проблемалық жағдаяттарды шешу арқылы оқушылардың бойында білім мен дағдылар қалыптастыру.

Сипаты: №№9.007, 9.008, / дәптерлеріне орындайды.

Оқушының іс-әрекеті: берілген тапсырманы орындайды, көмек қажет болған жағдайда сыныптастарынан не мұғалімнен көмек сұрайды.

Мұғалімнің іс-әрекеті: бағыттаушы, жетелеуші, қажетті жағдайда көмек беруші жұмысын атқарады.

Бағалау: Критерий бойынша бірін-бірі бағаланады.

7. Деңгейлік тест тапсырмасы. Жеке жұмыс

Мақсаты: оқушылардың бүгінгі сабақтың мақсатын қаншалықты және қандай деңгейде меңгергендігін бақылау.

Сипаты: Деңгейлік тапсырмасы екі жабық, бір ашық тест тапсырмасынан тұрады. Оқушылар өздерінің қалаған деңгейлеріне таңдап, тапсырмаларын орындайды.

Оқушының әрекеті: Өз қабілетін шынайы бағалап, сәйкес деңгейдің тапсырмасын орындайды.

Мұғалімнің әрекеті: Мұғалім бақылаушы, бағыттаушы қызметін атқарады.

Бағалау: Жауап экранға крсетіледі, оқушы өзін-өзін бағалайды.

Презентация

Презентация

.И.Сканави, 2500задач по математике с решениями 2007г/

Қосымша №2

Бағалау критерийі

Қосымша

№3 тест тапсырмасы

Сабақтың соңы

2 мин

8. Сабақты қорытындылап, рефлексия жүргізу. Өзін-өзі бағалау анализі

-Бүгінгі сабақта сен үшін жаңалық болған материалдар 2-3 мәлімет айтыңыз/нені білдім, нені үйрендім?/

-Сабақтың мақсаты қандай болды, тұжырымдап беріңіз. Сабақтың басында қойылған оқу мақсатына жеттім деп ойлайсың ба?/дәлелеңіз/

Қосымша ақпарат

Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз?

Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз?

Денсаулық және қауіпсіздік техникасының сақталуы

– Сұраққа жауап беруде қабілетті оқушылардын жауаптарын математикалық жолмен дәлелдеулерін талап етіледі;

– Қойылған сұрақтың қиындығына және жауаптың толықтығын қадағалап тексеріп отырамын;

–Ынталандыру, қолдау көрсету;

- Критерий бойынша бағалау бірін-бірі бағалайды;

- Дайын жауаппен өзін-өзі бағалайды.

Сабақ үстіндегі оқушылардың көңіл-күйін қадағалап отыру

Сабақ бойынша рефлексия

Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме?

Жеткізбесе, неліктен?

Сабақта саралау дұрыс жүргізілді ме?

Сабақтың уақыттық кезеңдері сақталды ма?

Сабақ жоспарынан қандай ауытқулар болды, неліктен?

Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз.