| Өтілген материалды қайталау. Мұғалім оқушыларға сұрақтар айтады. Оқушылар ауызша сұрақтарға жауап береді. (3 мин) 1. Жиынға мысал келтіріңіз. ( планеталар, мемлекеттер, әндер, теңдеулер, функциялар, фигуралар, т.б.) 2. Жиын және оның элементтері қалай белгіленеді? Жиынға тиісті обьект оның элементтері деп аталады. Жиынды латын бас әріпмен, ал оның элементтерін кіші әріппен белгіленеді. Кейде жиындарды белгілеуде фигуралық жақшалар қолданылады. 3. Жиындар қандай болады? Жиындар шекті және шексіз болады (элемент саны бойынша). Фигуралар, цифрлар – шекті жиын, ал түзудің бойындағы немесе кесіндідегі нүктелер жиыны; [2; 3], (-6; +∞) аралығындағы нақты сандар жиыны- шексіз. Қандай жиынды бос жиын деп атайды? Ешқандай элементі жоқ жиынды бос жиын деп атайды және оны 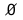 символымен белгілейді. символымен белгілейді. 4. Қандай жиындарды тең жиындар деп атайды? Егер жиын бірдей элементтерден тұрса, онда ондай жиынды тең деп атайды? 5. Ішкі жиын дегеніміз не? Егер А – жиыны В жиынының бөлігі болса онда оны В жиынының ішкі жиыны деп атайды және оны АВ деп белгілейді. 6. Екі жиынның бірігуі дегеніміз не? Егер К – А және В жиынының бірігуі болса, онда оны АВ = К деп жазады 7. Екі жиының қиылысуы дегеніміз не? Егер Р жиыны А және В жиындарының ортақ элементтерінен құралса, онда Р жиыны А және В жиынының қиылысуы деп аталады. Оны АВ = Р деп жазады. 8. А және В жиындарының айырмасы деп нені айтамыз? А және В жиынының айырмасы деп В жиынына тиісті емес А жиынның барлық элементтерін айтады. АВ деп белгілейді. 9. Мына жиындарға мысал келтіріңіз. 1) 3 элемент; 2) 7 элемент; 3) 10 элемент. Жауабы: 1) бағдаршамның түстер жиыны;
2) апта күндерінің жиыны; кемпірқосақ түстерінің жиыны;ноталар жиыны; 3) цифр жиыны.
Жаңа сабақты игерту. Мұғалім әңгіме түрінде оқушылардың назарын сабаққа аударады және олардан өз ойларын айтуға ынталандырады. ( 15 мин) Комбинаторика элементтері. Іс жүзінде кейбір заттардың өзара орналасуының барлық мүмкін жағдайлары санын, немесе қайсыбір әрекетіміздің барлық мүмкін нәтижелері санын есептеу, немесе оны орындаудың барлық мүмкін тәсілдері санын есептеу қажет болады. Мысалы, әр түрлі 5 оқулықты екі студент арасында неше түрлі тәсілмен үлестіріп беруге болады? Осындай есептерді комбинаторикалық есептер деп, ал комбинаторикалық есептерді оқып үйрететін матиматика саласын комбинаторика деп атайды. Комбинаторикалық есептерді шешу барысында қолданатын бірқатар заңдылықтар мен формулалар бар. Комбинаторика есептерін шешкенде мына ережелер қолданылады. Қосу ережесі. Егер А мен В объектілері тоғыспайтын болса және А объектісі m тәсілімен, ал В объектісі n тәсілімен алынса, онда
«А немесе В» объектілерін таңдау m + n тәсілмен жүзеге асады.
1-мысал . Математикадан оқушы ғылыми жобаны жазады. Оның таңдауына алгебрадан 17 тақырып, ал геометриядан -13 тақырып ұсынды. Қанша тәсілмен оқушы бір тақырыпты таңдай алады? Шешуі: Қосынды ережесі бойынша 17+13=30 тәсіл. Теорема: Кез келген санаулы элементтері бар А және В жиындары үшін 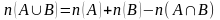 (1) теңдігі орындалады. (1) теңдігі орындалады. Салдар: Егер 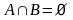 болса, онда болса, онда 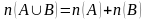 теңдігі орындалады. теңдігі орындалады. Дәлелдеу: 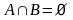 болғандықтан, болғандықтан, 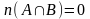 . Онда (1) формуладан көрсетілген теңдік шығады. . Онда (1) формуладан көрсетілген теңдік шығады. 2-мысал: Сыныптағы 32 оқушының 14-і мектепте өткен футбол турниріне, 10-ы баскетбол турниріне және 8-і волейбол ойынынан жарысқа қатысқан. Мұнда 6 оқушы әрі футбол, әрі баскетбол жарысына, 5 оқушы әрі футбол, әрі волейбол жарысына, 4 оқушы әрі баскетбол, әрі волейбол турниріне, ал 3 оқушы барлық үш ойыннан жарысқа қатысқан. Сынып оқушыларының нешеуі осы турнирлердің бірде-біреуіне қатыспаған? Жауабы: 12 оқушы.
Оқушыларға 3 -мысал беріледі. Бұл тапсырманы жұптасып орындайды. Әр жұптың тапсырманы қандай тәсілмен шығарғаны қадағаланады. Әртүрлі тәсілмен шығарған жұптар шешімдерін тақтада жазып көрсетеді. Оқушыларға көбейту ережесін өздері айтуы сұралады.
3-мысал. 0,1,2,4,5,9 цифрларынан қанша жұп екітаңбалы сандарды құрастыруға болады?
1-тәсіл: 10-нан 99-ға дейінгі сандардың арасынан бізге керек сандарды тізіп шығамыз: 10,12,14,20,22,24,40,42,44,50,52,54,90,92,94. Барлығы 15 сан. 2- тәсіл. Бірінші цифры 0 тұруы мүмкін емес, сондықтан егер бірінші орында- 1 цифры болса, онда екінші орында жұп цифр-0,2,4. Барлығы 3 мүмкіндік. Егер бірінші орында -2 цифры тұрса, онда да 3 вариант болады. Сонымен 4, 5,9 бірінші орында тұрғанда – әрбірінде 3 варианттан болады. Барлығы 5-тен 3 рет- 15тәсіл. 3- тәсіл: Бірінші орында тұратын цифрларының 5 тәсілі болады: 1,2,4,5,9. Екінші орынға жазудың 3 тәсілі болады: 0,2,4. Сондықтан 5×3=15.
Қай тәсіл тиімді екенін оқушылармен бірге талқылау. (3 тәсіл) Есептің шешуін кесте түрінде көрсетуге болады:
Көбейтінді ережесі бойынша А жəне В – ны n × m тəсілмен таңдап алуға болады: |
| 0 | 2 | 4 | | 1 | 10 | 12 | 14 | | 2 | 20 | 22 | 24 | | 4 | 40 | 42 | 44 | | 5 | 50 | 52 | 54 | | 9 | 90 | 92 | 94 | Мұғалім оқушылар жауабынан кейін ережені слайдтың көмегімен көрсетеді.
Көбейту ережесі. Егер А объектісі m әдіспен таңдалған болса және әрбір таңдамалардан кейін В объектісі n әдіспен таңдалса
(А таңдауынан тәуелсіз), онда А және В реттелген қостар таңдауын m×n әдісімен алуға болады. Теорема 2. Кез келген санаулы элементтері бар А және В жиындары үшін барлық, 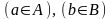 қос элементтер саны m осы жиындар элементтері сандарының көбейтіндісіне тең: қос элементтер саны m осы жиындар элементтері сандарының көбейтіндісіне тең: 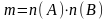 . . Бірлестіктің директорларының кеңесінің мүшелері арасынан үшеуі кеңес төралығына, ал екеуі оның орынбасары қызметіне сайлануға үміткер. Олардың ішінен неше түрлі тәсілдермен төраға мен орынбасарын сайлауға болады? Жауабы: 6
Сыныпта шығарылатын есептер. Берілген есептерді әр оқушы жеке орындайды, сосын жұбымен талқылайды. Мұғалім қадағалап жүріп бағалайды. (7 мин) Тапсырмалар. 1. Дүкенде алты түрлі шоколад және төрт түрлі карамель кәмпиттері бар. а) кәмпиттердің бір сортынан қанша кәмпиттер түрін сатып алуға болады? б) бір сорт шоколад және бір сорт карамель кәмпиттер түрлерін сатып алу үшін қанша жағдайлар болады?
Шешуі: Шоколад кәмпиттерін А объектісі арқылы, ал карамель кәмпиттерін В арқылы белгілейік. А объектісін 6 әдіспен, ал В объектісін 4 әдіспен алуға болады. а) А+В объектісі - кәмпиттің бір түрін алуға болатынын көрсетеді, яғни m+n = 6+4 =10 түрлі. б) 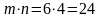 3. Қыздың 4 көйлегі, 5 юбка мен 3 аяқ қиімі бар. Қанша тәсілмен киімді таңдауға болады? (4×5×3=60 тәсіл.)
4. Таңғы тамаққа Арман тоқаш, бутерброд, пряник, кексті таңдай алады.Сусындардың арасында кофе, шырын және айран болды. Таңғы тамақты Арман қанша тәсілмен таңдай алады? (4×3=12 тәсіл) 5. Факториал. (10 мин)
Анықтама: бірден бастап n-ге дейінгі барлық натурал сандардың көбейтіндісін n факториал деп атаймыз және ол n! символымен белгіленеді.
 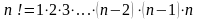 0! = 1 0! = 1 1-мысал. 1!=1 2!=1·2=2 3!=1·2·3=6 4!=1·2·3·4=24 5!=1·2·3·4·5=120
Келесі кестелерді есептер шығару да қолдануға болады: 1-мысал. Есептеңіз: а) 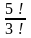 , b) , b) 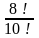 , c) , c) 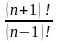 Шешуі. Факториалдың анықтамасын қолдана отырып табамыз, 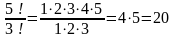 немесе 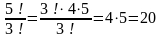 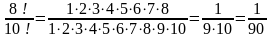
немесе 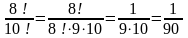 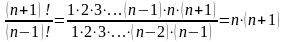
немесе 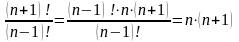
1. Сәйкестендіріңіз:
| 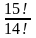
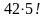
|
| 125 | | 9! | | 15 | | 7! | 2. Өрнекті ықшамдаңыз: 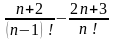 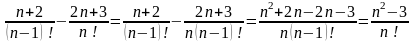
Үйге тапсырма: № 610, 612, 613. 1. Қорапта 12 ақ және 16 көк шарлар бар. Неше тәсілмен: а) кез келген түстегі бір шарды; б) екі әртүрлі түсті шарды алуға болады?
Шешуі. а) Қосындының ережесі бойынша кез келген түстегі бір шарды 12+16=28 (тәсілмен); б) көбейтінінің ережесі бойынша 16*12 =192 (тәсілмен) алуға болады. Жауабы: а) 28 ; 6) 192 тәсілмен. 2. сыныпта 15 ұл және12 қыз бар. Бір оқушы таңдалынған. Осыдан кейін неше тәсілмен қыз бен ұлды таңдауға болады?
Шешуі. Бір оқушы таңдалынған. Онда: а) егер ұлды таңдаса , онда ұлдар 14 және 14 нұсқа таңдалады, ал қыздар үшін 12 нұсқа таңдалады. 14*12=168 (тәсіл); б) егер қыз таңдалса, 11 қыз қалады, 11 нұсқа таңдалады. 11*15=165. Қосындының ережесі бойынша: 168 +165 = 333 (тәсіл). Жауабы: 333 тәсілмен. |